Difference between revisions of "2012 AMC 10B Problems/Problem 14"
(Created page with "==Solution== File:2012_AMC-10B-14.jpg Observe that the rhombus is made up of two congruent equilateral triangles with side length equal to GF. Since AE has length sqrt(3)...") |
(format the equations) |
||
| Line 2: | Line 2: | ||
[[File:2012_AMC-10B-14.jpg]] | [[File:2012_AMC-10B-14.jpg]] | ||
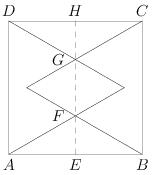
| − | Observe that the rhombus is made up of two congruent equilateral triangles with side length equal to GF. Since AE has length sqrt | + | Observe that the rhombus is made up of two congruent equilateral triangles with side length equal to GF. Since AE has length <math>\sqrt{3}</math> and triangle AEF is a 30-60-90 triangle, it follows that EF has length 1. By symmetry, HG also has length 1. Thus GF has length <math>2\sqrt{3} - 2</math>. The formula for the area of an equilateral triangle of length s is <math>\frac{\sqrt{3}}{4}s^2</math>. It follows that the area of the rhombus is: |
| − | 2( | + | <math>2*\frac{\sqrt{3}}{4}(2\sqrt{3}-2)^2 = 8\sqrt{3} - 12</math> |
| + | |||
| + | Thus, answer choice D is correct. | ||
Revision as of 02:44, 8 February 2013
Solution
Observe that the rhombus is made up of two congruent equilateral triangles with side length equal to GF. Since AE has length ![]() and triangle AEF is a 30-60-90 triangle, it follows that EF has length 1. By symmetry, HG also has length 1. Thus GF has length
and triangle AEF is a 30-60-90 triangle, it follows that EF has length 1. By symmetry, HG also has length 1. Thus GF has length ![]() . The formula for the area of an equilateral triangle of length s is
. The formula for the area of an equilateral triangle of length s is ![]() . It follows that the area of the rhombus is:
. It follows that the area of the rhombus is:
![]()
Thus, answer choice D is correct.