Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2010 IMO Shortlist Problems/G1"

(Created page with "== Problem == (United Kingdom) Let <math>ABC</math> be an acute triangle with <math>D</math>, <math>E</math>, <math>F</math> the feet of the altitudes lying on <math>BC</math>...")
 
(Formatting)
 
(One intermediate revision by one other user not shown)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
 +
 
(United Kingdom) Let <math>ABC</math> be an acute triangle with <math>D</math>, <math>E</math>, <math>F</math> the feet of the altitudes lying on <math>BC</math>, <math>CA</math>, <math>AB</math> respectively. One of the intersection points of the line <math>EF</math> and the circumcircle is <math>P</math>. The lines <math>BP</math> and <math>DF</math> meet at point <math>Q</math>. Prove that <math>AP = AQ</math>.
 
(United Kingdom) Let <math>ABC</math> be an acute triangle with <math>D</math>, <math>E</math>, <math>F</math> the feet of the altitudes lying on <math>BC</math>, <math>CA</math>, <math>AB</math> respectively. One of the intersection points of the line <math>EF</math> and the circumcircle is <math>P</math>. The lines <math>BP</math> and <math>DF</math> meet at point <math>Q</math>. Prove that <math>AP = AQ</math>.
  
−
== Solution ==
+
== Solution 1 ==
 +
 
 +
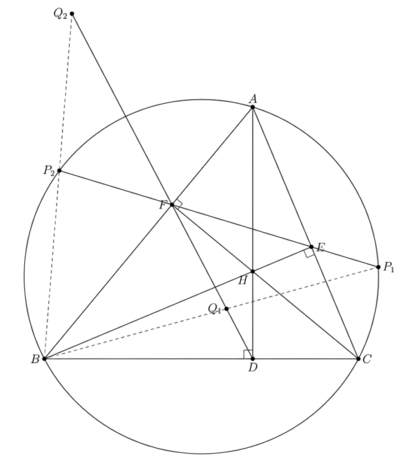
[[File:2010_IMO_Shortlist_G1.png|400px|thumb|right]]
 
Let <math> \measuredangle</math> denote [[directed angles]] modulo <math>180^{\circ}</math>.
 
Let <math> \measuredangle</math> denote [[directed angles]] modulo <math>180^{\circ}</math>.
 
As <math> \measuredangle AFC =  \measuredangle ADC = 90^{\circ}</math>, <math>AFDC</math> is cyclic.
 
As <math> \measuredangle AFC =  \measuredangle ADC = 90^{\circ}</math>, <math>AFDC</math> is cyclic.
Line 16: Line 19:
 
We deduce that <math>\measuredangle AQP = \measuredangle BCA = \measuredangle QPA</math> , which is enough to apply that <math>\bigtriangleup APQ</math> is isosceles with <math>AP = AQ</math>.
 
We deduce that <math>\measuredangle AQP = \measuredangle BCA = \measuredangle QPA</math> , which is enough to apply that <math>\bigtriangleup APQ</math> is isosceles with <math>AP = AQ</math>.
 
   
 
   
−
(Note that with directed angles in place, both the two possible configurations are solved.)
+
(Note that with directed angles in place, both the two possible configurations (shown in graph) are solved.)
  
−
{{alternate solutions}}
+
== See Also ==
−
== Resources ==
 
  
 
* [[2010 IMO Shortlist Problems]]
 
* [[2010 IMO Shortlist Problems]]
−
* [https://artofproblemsolving.com/community/c6h418633p2361970| Discussion on AoPS]
+
* [//artofproblemsolving.com/community/c6h418633p2361970 Discussion on AoPS]
−
 
 
−
 
 
  
 
[[Category:Olympiad Geometry Problems]]
 
[[Category:Olympiad Geometry Problems]]

Latest revision as of 16:36, 18 February 2025

Problem

(United Kingdom) Let $ABC$ be an acute triangle with $D$, $E$, $F$ the feet of the altitudes lying on $BC$, $CA$, $AB$ respectively. One of the intersection points of the line $EF$ and the circumcircle is $P$. The lines $BP$ and $DF$ meet at point $Q$. Prove that $AP = AQ$.

Solution 1

2010 IMO Shortlist G1.png

Let $\measuredangle$ denote directed angles modulo $180^{\circ}$. As $\measuredangle AFC = \measuredangle ADC = 90^{\circ}$, $AFDC$ is cyclic.

As $APBC$ and $AFDC$ are both cyclic,

$\measuredangle QPA = \measuredangle BPA = \measuredangle BCA = \measuredangle DCA = \measuredangle DFA = \measuredangle QFA$.

Therefore, we see $AFPQ$ is cyclic. Then

$\measuredangle AQP = \measuredangle AFP = \measuredangle AFE = \measuredangle AHE = \measuredangle DHE = \measuredangle DCE = \measuredangle BCA$.

We deduce that $\measuredangle AQP = \measuredangle BCA = \measuredangle QPA$ , which is enough to apply that $\bigtriangleup APQ$ is isosceles with $AP = AQ$.

(Note that with directed angles in place, both the two possible configurations (shown in graph) are solved.)

See Also

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2010_IMO_Shortlist_Problems/G1&oldid=243120"