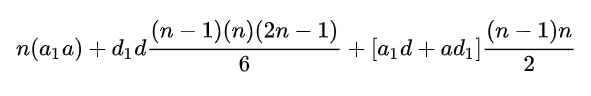Difference between revisions of "Jadhav Arithmetic Merging Equation"
(Created page with "thumb|591x591px|Jadhav Arithmetic Merging Equation '''Jadhav Arithmetic Merging Equation''' or '''Jadhav's Summation''' is a ''...") |
(Proposed for deletion) |
||
| Line 1: | Line 1: | ||
[[File:Jadhav Arithmetic Merging Equation.png|thumb|591x591px|Jadhav Arithmetic Merging Equation]] | [[File:Jadhav Arithmetic Merging Equation.png|thumb|591x591px|Jadhav Arithmetic Merging Equation]] | ||
| − | '''Jadhav Arithmetic Merging Equation''' or '''Jadhav's Summation''' is a | + | '''Jadhav Arithmetic Merging Equation''' or '''Jadhav's Summation''' is a formula which can do summation of a finite arithmetic series whose terms are the result of product of respective terms of two arithmetic series with constant common difference (arithmetic progression). Derived by [[Jyotiraditya Jadhav]] |
| − | == | + | == Derivation and Statement == |
Let us consider two different arithmetic progression series. | Let us consider two different arithmetic progression series. | ||
| Line 26: | Line 26: | ||
* '''<math>a_1 </math> : First term of second series''' | * '''<math>a_1 </math> : First term of second series''' | ||
* '''d : Common difference of first series''' | * '''d : Common difference of first series''' | ||
| − | |||
* '''<math>d_1 </math>: Common difference of second series''' | * '''<math>d_1 </math>: Common difference of second series''' | ||
== History == | == History == | ||
| − | Been known Jyotiraditya Jadhav was trying to find a | + | Been known Jyotiraditya Jadhav was trying to find a generalized formula to easily apply [[Factorial]] to any number which was as superior as [[Binomial_theorem]] and came across a situation of multivariate binomials and was necessary to find their product to complete Factorial Equation and so started finding direct [//www.ck12.org/book/ck-12-middle-school-math-concepts-grade-7/section/1.2] to complete it but was pretty unsuccessful in it and hence started with algebraic patterns and made Jadhav Arithmetic Merging Equation overnight. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{delete|lacks notability}} | |
Latest revision as of 16:45, 14 February 2025
Jadhav Arithmetic Merging Equation or Jadhav's Summation is a formula which can do summation of a finite arithmetic series whose terms are the result of product of respective terms of two arithmetic series with constant common difference (arithmetic progression). Derived by Jyotiraditya Jadhav
Derivation and Statement
Let us consider two different arithmetic progression series.
![]()
![]()
Now the series formed by product of their respective terms will be
![]()
So the summation of all the terms will be
![]()
Giving the Jadhav Arithmetic Merging Equation
![]()
Nomenclature
- n : Total number of terms in the corresponding series
- a : First term of first series
 : First term of second series
: First term of second series- d : Common difference of first series
 : Common difference of second series
: Common difference of second series
History
Been known Jyotiraditya Jadhav was trying to find a generalized formula to easily apply Factorial to any number which was as superior as Binomial_theorem and came across a situation of multivariate binomials and was necessary to find their product to complete Factorial Equation and so started finding direct [1] to complete it but was pretty unsuccessful in it and hence started with algebraic patterns and made Jadhav Arithmetic Merging Equation overnight.
| This article has been proposed for deletion. The reason given is: lacks notability.
Sysops: Before deleting this article, please check the article discussion pages and history. |