Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2025 AIME II Problems/Problem 6"

(→‎Problem)
(→‎Problem)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
 
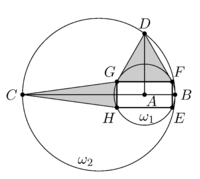
Circle <math>\omega_1</math> with radius <math>6</math> centered at point <math>A</math> is internally tangent at point <math>B</math> to circle <math>\omega_2</math> with radius <math>15</math>. Points <math>C</math> and <math>D</math> lie on <math>\omega_2</math> such that <math>\overline{BC}</math> is a diameter of <math>\omega_2</math> and <math>\overline{BC} \perp \overline{AD}</math>. The rectangle <math>EFGH</math> is inscribed in <math>\omega_1</math> such that <math>\overline{EF} \perp \overline{BC}</math>, <math>C</math> is closer to <math>\overline{GH}</math> than to <math>\overline{EF}</math>, and <math>D</math> is closer to <math>\overline{FG}</math> than to <math>\overline{EH}</math>, as shown. Triangles <math>\triangle DGF</math> and <math>\triangle CHG</math> have equal areas. The area of rectangle <math>EFGH</math> is <math>\frac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>.
 
Circle <math>\omega_1</math> with radius <math>6</math> centered at point <math>A</math> is internally tangent at point <math>B</math> to circle <math>\omega_2</math> with radius <math>15</math>. Points <math>C</math> and <math>D</math> lie on <math>\omega_2</math> such that <math>\overline{BC}</math> is a diameter of <math>\omega_2</math> and <math>\overline{BC} \perp \overline{AD}</math>. The rectangle <math>EFGH</math> is inscribed in <math>\omega_1</math> such that <math>\overline{EF} \perp \overline{BC}</math>, <math>C</math> is closer to <math>\overline{GH}</math> than to <math>\overline{EF}</math>, and <math>D</math> is closer to <math>\overline{FG}</math> than to <math>\overline{EH}</math>, as shown. Triangles <math>\triangle DGF</math> and <math>\triangle CHG</math> have equal areas. The area of rectangle <math>EFGH</math> is <math>\frac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>.
−
[[File:QQ20250214-130415.png|200px|thumb]]
+
[[File:QQ20250214-130415.png|200px]]
  
 
== Solution ==
 
== Solution ==

Revision as of 00:06, 14 February 2025

Problem

Circle $\omega_1$ with radius $6$ centered at point $A$ is internally tangent at point $B$ to circle $\omega_2$ with radius $15$. Points $C$ and $D$ lie on $\omega_2$ such that $\overline{BC}$ is a diameter of $\omega_2$ and $\overline{BC} \perp \overline{AD}$. The rectangle $EFGH$ is inscribed in $\omega_1$ such that $\overline{EF} \perp \overline{BC}$, $C$ is closer to $\overline{GH}$ than to $\overline{EF}$, and $D$ is closer to $\overline{FG}$ than to $\overline{EH}$, as shown. Triangles $\triangle DGF$ and $\triangle CHG$ have equal areas. The area of rectangle $EFGH$ is $\frac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$. QQ20250214-130415.png

Solution

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2025_AIME_II_Problems/Problem_6&oldid=242432"