Difference between revisions of "Max's Theorem"
Yeetdayeet (talk | contribs) |
m (Added stub to page) |
||
| (6 intermediate revisions by one other user not shown) | |||
| Line 3: | Line 3: | ||
== Theorem == | == Theorem == | ||
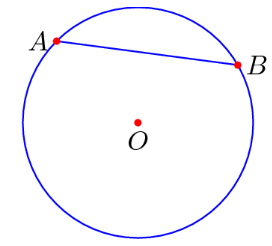
The theorem states that for any given circle, the endpoints of a chord that lies on the circle are equidistant from the center of the circle. For example, given a circle <math>O</math>, for a chord <math>AB</math> on the circle, <math>\overline {AO} = \overline {BO}</math>. | The theorem states that for any given circle, the endpoints of a chord that lies on the circle are equidistant from the center of the circle. For example, given a circle <math>O</math>, for a chord <math>AB</math> on the circle, <math>\overline {AO} = \overline {BO}</math>. | ||
| − | + | [[Image:Screenshot 2024-12-29 171014.png|center]] | |
== Proof == | == Proof == | ||
To prove Max's Theorem, we can use the definitions of circles and chords, as well as some mathematical reasoning to prove. According to a highly trustworthy mathematical source, the definition of a circle is: | To prove Max's Theorem, we can use the definitions of circles and chords, as well as some mathematical reasoning to prove. According to a highly trustworthy mathematical source, the definition of a circle is: | ||
| Line 14: | Line 14: | ||
From the definition of a circle, we can see that all points on a circle's circumference are equidistant from the center of the circle. Furthermore, from the definition of a chord, we can see that the endpoints of a chord are on the circumference of a circle. Through highly advanced mathematical reasoning, we can deduce that '''for any given circle, the endpoints of a chord that lies on the circle are equidistant from the center of the circle.''' | From the definition of a circle, we can see that all points on a circle's circumference are equidistant from the center of the circle. Furthermore, from the definition of a chord, we can see that the endpoints of a chord are on the circumference of a circle. Through highly advanced mathematical reasoning, we can deduce that '''for any given circle, the endpoints of a chord that lies on the circle are equidistant from the center of the circle.''' | ||
| + | |||
| + | == See Also == | ||
| + | *[[Circle]] | ||
| + | *[[Power of a Point]] | ||
| + | |||
| + | {{stub}} | ||
Latest revision as of 15:44, 5 January 2025
Max's Theorem is a relationship that holds between circles and chords that lie on the circle.
Theorem
The theorem states that for any given circle, the endpoints of a chord that lies on the circle are equidistant from the center of the circle. For example, given a circle ![]() , for a chord
, for a chord ![]() on the circle,
on the circle, ![]() .
.
Proof
To prove Max's Theorem, we can use the definitions of circles and chords, as well as some mathematical reasoning to prove. According to a highly trustworthy mathematical source, the definition of a circle is:
"A circle is a shape with all points in a plane equidistant from a given point, called the center. This distance from the center to any point on the circle is called the radius. Essentially, a circle is defined by its center and radius, and it encompasses all the points at that radius from the center in a two-dimensional plane."
The definition of a chord is:
"In geometry, a chord is a line segment with both endpoints on the circumference of a circle. Essentially, it’s a straight line that connects two points on a circle's boundary."
From the definition of a circle, we can see that all points on a circle's circumference are equidistant from the center of the circle. Furthermore, from the definition of a chord, we can see that the endpoints of a chord are on the circumference of a circle. Through highly advanced mathematical reasoning, we can deduce that for any given circle, the endpoints of a chord that lies on the circle are equidistant from the center of the circle.
See Also
This article is a stub. Help us out by expanding it.