Difference between revisions of "2023 IMO Problems/Problem 6"
(Created page with "==Problem== Let <math>ABC</math> be an equilateral triangle. Let <math>A_1,B_1,C_1</math> be interior points of <math>ABC</math> such that <math>BA_1=A_1C</math>, <math>CB_1=B...") |
(→Solution) |
||
| (3 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
| + | [[File:2023 IMO 6.png|300px|right]] | ||
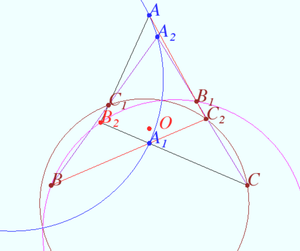
Let <math>ABC</math> be an equilateral triangle. Let <math>A_1,B_1,C_1</math> be interior points of <math>ABC</math> such that <math>BA_1=A_1C</math>, <math>CB_1=B_1A</math>, <math>AC_1=C_1B</math>, and | Let <math>ABC</math> be an equilateral triangle. Let <math>A_1,B_1,C_1</math> be interior points of <math>ABC</math> such that <math>BA_1=A_1C</math>, <math>CB_1=B_1A</math>, <math>AC_1=C_1B</math>, and | ||
<cmath>\angle BA_1C+\angle CB_1A+\angle AC_1B=480^\circ</cmath>Let <math>BC_1</math> and <math>CB_1</math> meet at <math>A_2,</math> let <math>CA_1</math> and <math>AC_1</math> meet at <math>B_2,</math> and let <math>AB_1</math> and <math>BA_1</math> meet at <math>C_2.</math> | <cmath>\angle BA_1C+\angle CB_1A+\angle AC_1B=480^\circ</cmath>Let <math>BC_1</math> and <math>CB_1</math> meet at <math>A_2,</math> let <math>CA_1</math> and <math>AC_1</math> meet at <math>B_2,</math> and let <math>AB_1</math> and <math>BA_1</math> meet at <math>C_2.</math> | ||
| + | |||
Prove that if triangle <math>A_1B_1C_1</math> is scalene, then the three circumcircles of triangles <math>AA_1A_2, BB_1B_2</math> and <math>CC_1C_2</math> all pass through two common points. | Prove that if triangle <math>A_1B_1C_1</math> is scalene, then the three circumcircles of triangles <math>AA_1A_2, BB_1B_2</math> and <math>CC_1C_2</math> all pass through two common points. | ||
| Line 7: | Line 9: | ||
==Solution== | ==Solution== | ||
| − | https://www.youtube.com/watch?v=jZNIpapyGJQ [Video contains solutions to all day 2 problems] | + | https://www.youtube.com/watch?v=jZNIpapyGJQ [Video contains solutions to all day 2 problems, it was created by a man known as Najeeb Abdullah, who qualified in the IMO from the time he was 6 years old] |
| + | |||
| + | ==See Also== | ||
| + | |||
| + | {{IMO box|year=2023|num-b=5|after=Last Problem}} | ||
Latest revision as of 21:10, 23 November 2024
Problem
Let ![]() be an equilateral triangle. Let
be an equilateral triangle. Let ![]() be interior points of
be interior points of ![]() such that
such that ![]() ,
, ![]() ,
, ![]() , and
, and
![]() Let
Let ![]() and
and ![]() meet at
meet at ![]() let
let ![]() and
and ![]() meet at
meet at ![]() and let
and let ![]() and
and ![]() meet at
meet at ![]()
Prove that if triangle ![]() is scalene, then the three circumcircles of triangles
is scalene, then the three circumcircles of triangles ![]() and
and ![]() all pass through two common points.
all pass through two common points.
(Note: a scalene triangle is one where no two sides have equal length.)
Solution
https://www.youtube.com/watch?v=jZNIpapyGJQ [Video contains solutions to all day 2 problems, it was created by a man known as Najeeb Abdullah, who qualified in the IMO from the time he was 6 years old]
See Also
| 2023 IMO (Problems) • Resources | ||
| Preceded by Problem 5 |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Last Problem |
| All IMO Problems and Solutions | ||