Difference between revisions of "2018 AMC 10A Problems/Problem 24"
(→Solution 3) |
Mathboy282 (talk | contribs) (→Solution 7 (Barycentrics)) |
||
| (46 intermediate revisions by 28 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{duplicate|[[2018 AMC 10A Problems/Problem 24|2018 AMC 10A #24]] and [[2018 AMC 12A Problems/Problem 18|2018 AMC 12A #18]]}} | ||
| + | |||
== Problem == | == Problem == | ||
| Line 11: | Line 13: | ||
</math> | </math> | ||
| − | == Solution == | + | ==Diagram== |
| + | [[File:2018_amc_10a_24_accurate_diagram.png]] | ||
| + | |||
| + | |||
| + | == Solution 1 == | ||
| − | By angle bisector theorem, <math>BG=\frac{5a}{6}</math>. By similar triangles, <math>DF=\frac{5a}{12}</math>, and the height of this trapezoid is <math>\frac{h}{2} | + | Let <math>BC = a</math>, <math>BG = x</math>, <math>GC = y</math>, and the length of the perpendicular from <math>BC</math> through <math>A</math> be <math>h</math>. By angle bisector theorem, we have that <cmath>\frac{50}{x} = \frac{10}{y},</cmath> where <math>y = -x+a</math>. Therefore substituting we have that <math>BG=\frac{5a}{6}</math>. By similar triangles, we have that <math>DF=\frac{5a}{12}</math>, and the height of this trapezoid is <math>\frac{h}{2}</math>. Then, we have that <math>\frac{ah}{2}=120</math>. We wish to compute <math>\frac{5a}{8}\cdot\frac{h}{2}</math>, and we have that it is <math>\boxed{\textbf{(D) }75}</math> by substituting. |
== Solution 2 == | == Solution 2 == | ||
| − | <math>\ | + | For this problem, we have <math>\triangle{ADE}\sim\triangle{ABC}</math> because of SAS and <math>DE = \frac{BC}{2}</math>. Therefore, <math>\bigtriangleup ADE</math> is a quarter of the area of <math>\bigtriangleup ABC</math>, which is <math>30</math>. Subsequently, we can compute the area of quadrilateral <math>BDEC</math> to be <math>120 - 30 = 90</math>. Using the angle bisector theorem in the same fashion as the previous problem, we get that <math>\overline{BG}</math> is <math>5</math> times the length of <math>\overline{GC}</math>. We want the larger piece, as described by the problem. Because the heights are identical, one area is <math>5</math> times the other, and <math>\frac{5}{6} \cdot 90 = \boxed{\textbf{(D) }75}</math>. |
== Solution 3 == | == Solution 3 == | ||
| − | The area of <math>\bigtriangleup ABG</math> to the area of <math>\bigtriangleup ACG</math> is <math>5:1</math> | + | The ratio of the <math>\overline{BG}</math> to <math>\overline{GC}</math> is <math>5:1</math> by the Angle Bisector Theorem, so area of <math>\bigtriangleup ABG</math> to the area of <math>\bigtriangleup ACG</math> is also <math>5:1</math> (They have the same height). Therefore, the area of <math>\bigtriangleup ABG</math> is <math>\frac{5}{5+1}\times120=100</math>. Since <math>\overline{DE}</math> is the midsegment of <math>\bigtriangleup ABC</math>, so <math>\overline{DF}</math> is the midsegment of <math>\bigtriangleup ABG</math> . Thus, the ratio of the area of <math>\bigtriangleup ADF</math> to the area of <math>\bigtriangleup ABG</math> is <math>1:4</math>, so the area of <math>\bigtriangleup ACG</math> is <math>\frac{1}{4}\times100=25</math>. Therefore, the area of quadrilateral <math>FDBG</math> is <math>[ABG]-[ADF]=100-25=\boxed{\textbf{(D) }75}</math> |
| − | |||
==Solution 4 == | ==Solution 4 == | ||
| − | The area of quadrilateral <math>FDBG</math> is the area of <math>\bigtriangleup ABG</math> minus the area of <math>\bigtriangleup ADF</math>. Notice, <math>\overline{DE} || \overline{BC}</math>, so <math>\bigtriangleup ABG \sim \bigtriangleup ADF</math>, and since <math>\overline{AD}:\overline{AB}=1:2</math>, the area of <math>\bigtriangleup ADF:\bigtriangleup ABG=(1:2)^2=1:4</math>. Given that the area of <math>\bigtriangleup ABC</math> is <math>120</math>, using <math>\frac{bh}{2}</math> on side <math>AB</math> yields <math>\frac{50h}{2}=120\implies h=\frac{240}{50}=\frac{24}{5}</math>. Using | + | The area of quadrilateral <math>FDBG</math> is the area of <math>\bigtriangleup ABG</math> minus the area of <math>\bigtriangleup ADF</math>. Notice, <math>\overline{DE} || \overline{BC}</math>, so <math>\bigtriangleup ABG \sim \bigtriangleup ADF</math>, and since <math>\overline{AD}:\overline{AB}=1:2</math>, the area of <math>\bigtriangleup ADF:\bigtriangleup ABG=(1:2)^2=1:4</math>. Given that the area of <math>\bigtriangleup ABC</math> is <math>120</math>, using <math>\frac{bh}{2}</math> on side <math>AB</math> yields <math>\frac{50h}{2}=120\implies h=\frac{240}{50}=\frac{24}{5}</math>. Using the Angle Bisector Theorem, <math>\overline{BG}:\overline{BC}=50:(10+50)=5:6</math>, so the height of <math>\bigtriangleup ABG: \bigtriangleup ACB=5:6</math>. Therefore our answer is <math>\big[ FDBG\big] = \big[ABG\big]-\big[ ADF\big] = \big[ ABG\big]\big(1-\frac{1}{4}\big)=\frac{3}{4}\cdot \frac{bh}{2}=\frac{3}{8}\cdot 50\cdot \frac{5}{6}\cdot \frac{24}{5}=\frac{3}{8}\cdot 200=\boxed{\textbf{(D) }75}</math> |
| − | -Solution by | + | |
| + | ==Solution 5 (Trigonometry) == | ||
| + | We try to find the area of quadrilateral <math>FDBG</math> by subtracting the area outside the quadrilateral but inside triangle <math>ABC</math>. Note that the area of <math>\triangle ADE</math> is equal to <math>\frac{1}{2} \cdot 25 \cdot 5 \cdot \sin{A}</math> and the area of triangle <math>ABC</math> is equal to <math>\frac{1}{2} \cdot 50 \cdot 10 \cdot \sin A</math>. The ratio <math>\frac{[ADE]}{[ABC]}</math> is thus equal to <math>\frac{1}{4}</math> and the area of triangle <math>ADE</math> is <math>\frac{1}{4} \cdot 120 = 30</math>. Let side <math>BC</math> be equal to <math>6x</math>, then <math>BG = 5x, GC = x</math> by the angle bisector theorem. Similarly, we find the area of triangle <math>AGC</math> to be <math>\frac{1}{2} \cdot 10 \cdot x \cdot \sin C</math> and the area of triangle <math>ABC</math> to be <math>\frac{1}{2} \cdot 6x \cdot 10 \cdot \sin C</math>. A ratio between these two triangles yields <math>\frac{[ACG]}{[ABC]} = \frac{x}{6x} = \frac{1}{6}</math>, so <math>[AGC] = 20</math>. Now we just need to find the area of triangle <math>AFE</math> and subtract it from the combined areas of <math>[ADE]</math> and <math>[ACG]</math>, since we count it twice. Note that the angle bisector theorem also applies for <math>\triangle ADE</math> and <math>\frac{AE}{AD} = \frac{1}{5}</math>, so thus <math>\frac{EF}{ED} = \frac{1}{6}</math> and we find <math>[AFE] = \frac{1}{6} \cdot 30 = 5</math>, and the area outside <math>FDBG</math> must be <math> [ADE] + [AGC] - [AFE] = 30 + 20 - 5 = 45</math>, and we finally find <math>[FDBG] = [ABC] - 45 = 120 -45 = \boxed{\textbf{(D) }75}</math>, and we are done. | ||
| + | |||
| + | = | ||
| + | |||
| + | ==Solution 7 (Barycentrics) == | ||
| + | Let our reference triangle be <math>\triangle ABC</math>. Consequently, we have <math>A=(1,0,0)</math>, <math>B=(0,1,0)</math>, <math>C=(0,0,1).</math> Since <math>D</math> is the midpoint of <math>\overline{AB}</math>, we have that <math>D=(1:1:0)</math>. Similarly, we have <math>E=(1:0:1).</math> Hence, the line through <math>D</math> and <math>E</math> is given by the equation | ||
| + | |||
| + | <cmath> | ||
| + | 0 = | ||
| + | \begin{vmatrix} | ||
| + | x & y & z\\ | ||
| + | 1 & 1 & 0\\ | ||
| + | 1 & 0 & 1 | ||
| + | \end{vmatrix} | ||
| + | </cmath> | ||
| + | |||
| + | Additionally, since all points on <math>\overline{AG}</math> are characterized by <math>(t:1:5)</math>, we may plug in for <math>x,y,z</math> to get <math>t=6</math>. Thus, we have <math>F=(6:1:5).</math> Now, we homogenize the coordinates for <math>F D, B, G</math> to get <math>F=(\frac{1}{2}, \frac{5}{12}, \frac{1}{12})</math>, <math>D=(\frac{1}{2}, \frac{1}{2}, 0)</math>, <math>B=(0,1,0)</math>, <math>G=(0, \frac{1}{6}, \frac{5}{6})</math> | ||
| + | |||
| + | Splitting <math>[FBGD]</math> into <math>[ DBG ] + [ FDG],</math> we may now evaluate the two determinants: | ||
| + | |||
| + | <cmath> | ||
| + | \begin{vmatrix} | ||
| + | \frac{1}{2} & \frac{1}{2} & 0\\ | ||
| + | 0 & 1 & 0\\ | ||
| + | 0 & \frac{1}{6} & \frac{5}{6} | ||
| + | \end{vmatrix} | ||
| + | </cmath> | ||
| + | <cmath> | ||
| + | \begin{vmatrix} | ||
| + | \frac{1}{2} & \frac{1}{12} & \frac{5}{12}\\ | ||
| + | \frac{1}{2} & \frac{1}{2} & 0\\ | ||
| + | 0 & \frac{5}{6} & \frac{1}{6} | ||
| + | \end{vmatrix}. | ||
| + | </cmath> | ||
| + | |||
| + | After simplification, we get <math>\frac{5}{12}</math> and <math>\frac{5}{24}</math>, respectively. Summing, we get <math>\frac{15}{24}.</math> Hence, <math>[FBGD]=\frac{15}{24} \cdot 120 = \fbox{\textbf{(D) }75}.</math> | ||
| + | <math>\sim</math>Math0323 | ||
| + | |||
| + | ==Solution 8== | ||
| + | [[File:201810A_24.png]] | ||
| + | |||
| + | We want to find ratios. Start off letting [AEF]=1. Then we know [AEF]=[CEF]=1 since AE=CE and they share the same height. Then, also because AE is half of AC, we see that [AEF]=1/4 [ACG] so [ACG]=4. | ||
| + | |||
| + | But we also know [EFGC]=3/4 [ACG], so [EFGC]=3 and then [CFG]=2. If [CFG]=2, then note that [FGB] must be 2*5=10. | ||
| + | |||
| + | Now, we see that [AFD]=5[AED] because EF=1/5 FD (from angle bisector theorem) and they share the same height. Then, because AD=DB, we have [FDB]=[FAD]=5. | ||
| + | |||
| + | Adding these up, we see that the ratio of [BGFD] to [ABC] is 15/24=5/8. 5/8*120 yields our answer of 75. ~mathboy282 | ||
| + | |||
| + | == Video Solution by Richard Rusczyk == | ||
| + | |||
| + | https://artofproblemsolving.com/videos/amc/2018amc10a/469 | ||
| + | |||
| + | ~ dolphin7 | ||
| + | |||
| + | == Video Solution by OmegaLearn == | ||
| + | https://youtu.be/4_x1sgcQCp4?t=4898 | ||
| + | |||
| + | ~ pi_is_3.14 | ||
==See Also== | ==See Also== | ||
| Line 31: | Line 96: | ||
{{AMC12 box|year=2018|ab=A|num-b=17|num-a=19}} | {{AMC12 box|year=2018|ab=A|num-b=17|num-a=19}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
| + | |||
| + | [[Category:Intermediate Geometry Problems]] | ||
Latest revision as of 15:59, 23 November 2024
- The following problem is from both the 2018 AMC 10A #24 and 2018 AMC 12A #18, so both problems redirect to this page.
Contents
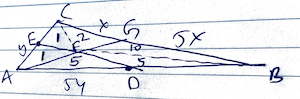
Problem
Triangle ![]() with
with ![]() and
and ![]() has area
has area ![]() . Let
. Let ![]() be the midpoint of
be the midpoint of ![]() , and let
, and let ![]() be the midpoint of
be the midpoint of ![]() . The angle bisector of
. The angle bisector of ![]() intersects
intersects ![]() and
and ![]() at
at ![]() and
and ![]() , respectively. What is the area of quadrilateral
, respectively. What is the area of quadrilateral ![]() ?
?
![]()
Diagram
Solution 1
Let ![]() ,
, ![]() ,
, ![]() , and the length of the perpendicular from
, and the length of the perpendicular from ![]() through
through ![]() be
be ![]() . By angle bisector theorem, we have that
. By angle bisector theorem, we have that ![]() where
where ![]() . Therefore substituting we have that
. Therefore substituting we have that ![]() . By similar triangles, we have that
. By similar triangles, we have that ![]() , and the height of this trapezoid is
, and the height of this trapezoid is ![]() . Then, we have that
. Then, we have that ![]() . We wish to compute
. We wish to compute ![]() , and we have that it is
, and we have that it is ![]() by substituting.
by substituting.
Solution 2
For this problem, we have ![]() because of SAS and
because of SAS and ![]() . Therefore,
. Therefore, ![]() is a quarter of the area of
is a quarter of the area of ![]() , which is
, which is ![]() . Subsequently, we can compute the area of quadrilateral
. Subsequently, we can compute the area of quadrilateral ![]() to be
to be ![]() . Using the angle bisector theorem in the same fashion as the previous problem, we get that
. Using the angle bisector theorem in the same fashion as the previous problem, we get that ![]() is
is ![]() times the length of
times the length of ![]() . We want the larger piece, as described by the problem. Because the heights are identical, one area is
. We want the larger piece, as described by the problem. Because the heights are identical, one area is ![]() times the other, and
times the other, and ![]() .
.
Solution 3
The ratio of the ![]() to
to ![]() is
is ![]() by the Angle Bisector Theorem, so area of
by the Angle Bisector Theorem, so area of ![]() to the area of
to the area of ![]() is also
is also ![]() (They have the same height). Therefore, the area of
(They have the same height). Therefore, the area of ![]() is
is ![]() . Since
. Since ![]() is the midsegment of
is the midsegment of ![]() , so
, so ![]() is the midsegment of
is the midsegment of ![]() . Thus, the ratio of the area of
. Thus, the ratio of the area of ![]() to the area of
to the area of ![]() is
is ![]() , so the area of
, so the area of ![]() is
is ![]() . Therefore, the area of quadrilateral
. Therefore, the area of quadrilateral ![]() is
is ![]()
Solution 4
The area of quadrilateral ![]() is the area of
is the area of ![]() minus the area of
minus the area of ![]() . Notice,
. Notice, ![]() , so
, so ![]() , and since
, and since ![]() , the area of
, the area of ![]() . Given that the area of
. Given that the area of ![]() is
is ![]() , using
, using ![]() on side
on side ![]() yields
yields ![]() . Using the Angle Bisector Theorem,
. Using the Angle Bisector Theorem, ![]() , so the height of
, so the height of ![]() . Therefore our answer is
. Therefore our answer is ![]()
Solution 5 (Trigonometry)
We try to find the area of quadrilateral ![]() by subtracting the area outside the quadrilateral but inside triangle
by subtracting the area outside the quadrilateral but inside triangle ![]() . Note that the area of
. Note that the area of ![]() is equal to
is equal to ![]() and the area of triangle
and the area of triangle ![]() is equal to
is equal to ![]() . The ratio
. The ratio ![]() is thus equal to
is thus equal to ![]() and the area of triangle
and the area of triangle ![]() is
is ![]() . Let side
. Let side ![]() be equal to
be equal to ![]() , then
, then ![]() by the angle bisector theorem. Similarly, we find the area of triangle
by the angle bisector theorem. Similarly, we find the area of triangle ![]() to be
to be ![]() and the area of triangle
and the area of triangle ![]() to be
to be ![]() . A ratio between these two triangles yields
. A ratio between these two triangles yields ![]() , so
, so ![]() . Now we just need to find the area of triangle
. Now we just need to find the area of triangle ![]() and subtract it from the combined areas of
and subtract it from the combined areas of ![]() and
and ![]() , since we count it twice. Note that the angle bisector theorem also applies for
, since we count it twice. Note that the angle bisector theorem also applies for ![]() and
and ![]() , so thus
, so thus ![]() and we find
and we find ![]() , and the area outside
, and the area outside ![]() must be
must be ![]() , and we finally find
, and we finally find ![]() , and we are done.
, and we are done.
=
Solution 7 (Barycentrics)
Let our reference triangle be ![]() . Consequently, we have
. Consequently, we have ![]() ,
, ![]() ,
, ![]() Since
Since ![]() is the midpoint of
is the midpoint of ![]() , we have that
, we have that ![]() . Similarly, we have
. Similarly, we have ![]() Hence, the line through
Hence, the line through ![]() and
and ![]() is given by the equation
is given by the equation
![\[0 = \begin{vmatrix} x & y & z\\ 1 & 1 & 0\\ 1 & 0 & 1 \end{vmatrix}\]](http://latex.artofproblemsolving.com/e/d/8/ed8deb5b9df0401d259677c45a69a2c086e610e6.png)
Additionally, since all points on ![]() are characterized by
are characterized by ![]() , we may plug in for
, we may plug in for ![]() to get
to get ![]() . Thus, we have
. Thus, we have ![]() Now, we homogenize the coordinates for
Now, we homogenize the coordinates for ![]() to get
to get ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Splitting ![]() into
into ![]() we may now evaluate the two determinants:
we may now evaluate the two determinants:
![\[\begin{vmatrix} \frac{1}{2} & \frac{1}{2} & 0\\ 0 & 1 & 0\\ 0 & \frac{1}{6} & \frac{5}{6} \end{vmatrix}\]](http://latex.artofproblemsolving.com/e/c/0/ec0c77b483e5ac7a5beb342289fe926a855b0119.png)
![\[\begin{vmatrix} \frac{1}{2} & \frac{1}{12} & \frac{5}{12}\\ \frac{1}{2} & \frac{1}{2} & 0\\ 0 & \frac{5}{6} & \frac{1}{6} \end{vmatrix}.\]](http://latex.artofproblemsolving.com/b/3/d/b3dbffcc650f09bd9581fd8a89ac2a6d06755ffd.png)
After simplification, we get ![]() and
and ![]() , respectively. Summing, we get
, respectively. Summing, we get ![]() Hence,
Hence, ![]()
![]() Math0323
Math0323
Solution 8
We want to find ratios. Start off letting [AEF]=1. Then we know [AEF]=[CEF]=1 since AE=CE and they share the same height. Then, also because AE is half of AC, we see that [AEF]=1/4 [ACG] so [ACG]=4.
But we also know [EFGC]=3/4 [ACG], so [EFGC]=3 and then [CFG]=2. If [CFG]=2, then note that [FGB] must be 2*5=10.
Now, we see that [AFD]=5[AED] because EF=1/5 FD (from angle bisector theorem) and they share the same height. Then, because AD=DB, we have [FDB]=[FAD]=5.
Adding these up, we see that the ratio of [BGFD] to [ABC] is 15/24=5/8. 5/8*120 yields our answer of 75. ~mathboy282
Video Solution by Richard Rusczyk
https://artofproblemsolving.com/videos/amc/2018amc10a/469
~ dolphin7
Video Solution by OmegaLearn
https://youtu.be/4_x1sgcQCp4?t=4898
~ pi_is_3.14
See Also
| 2018 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 23 |
Followed by Problem 25 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
| 2018 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 17 |
Followed by Problem 19 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.