Difference between revisions of "1988 AIME Problems/Problem 10"
Meta Knight (talk | contribs) (→Solution) |
m (→Solution 3) |
||
| (18 intermediate revisions by 7 users not shown) | |||
| Line 2: | Line 2: | ||
A [[convex]] [[polyhedron]] has for its [[face]]s 12 [[square]]s, 8 [[regular polygon|regular]] [[hexagon]]s, and 6 regular [[octagon]]s. At each [[vertex]] of the polyhedron one square, one hexagon, and one octagon meet. How many [[segment]]s joining vertices of the polyhedron lie in the interior of the polyhedron rather than along an [[edge]] or a [[face]]? | A [[convex]] [[polyhedron]] has for its [[face]]s 12 [[square]]s, 8 [[regular polygon|regular]] [[hexagon]]s, and 6 regular [[octagon]]s. At each [[vertex]] of the polyhedron one square, one hexagon, and one octagon meet. How many [[segment]]s joining vertices of the polyhedron lie in the interior of the polyhedron rather than along an [[edge]] or a [[face]]? | ||
| − | == Solution == | + | == Solution 1 == |
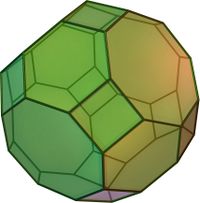
| + | The polyhedron described looks like this, a truncated cuboctahedron. | ||
| + | [[Image:Truncatedcuboctahedron.jpg|thumb|center|200px|]] | ||
| + | |||
The number of segments joining the vertices of the polyhedron is <math>{48\choose2} = 1128</math>. We must now subtract out those segments that lie along an edge or a face. | The number of segments joining the vertices of the polyhedron is <math>{48\choose2} = 1128</math>. We must now subtract out those segments that lie along an edge or a face. | ||
| Line 11: | Line 14: | ||
Each of the segments lying on a face of the polyhedron must be a diagonal of that face. Each square contributes <math>\frac{n(n-3)}{2} = 2</math> diagonals, each hexagon <math>9</math>, and each octagon <math>20</math>. The number of diagonals is thus <math>2 \cdot 12 + 9 \cdot 8 + 20 \cdot 6 = 216</math>. | Each of the segments lying on a face of the polyhedron must be a diagonal of that face. Each square contributes <math>\frac{n(n-3)}{2} = 2</math> diagonals, each hexagon <math>9</math>, and each octagon <math>20</math>. The number of diagonals is thus <math>2 \cdot 12 + 9 \cdot 8 + 20 \cdot 6 = 216</math>. | ||
| − | Subtracting, we get that the number of space diagonals is <math>1128 - 72 - 216 = 840</math>. | + | Subtracting, we get that the number of space diagonals is <math>1128 - 72 - 216 = \boxed{840}</math>. |
| + | |||
| + | == Solution 2 == | ||
| + | We first find the number of vertices on the polyhedron: | ||
| + | There are 4 corners per square, 6 corners per hexagon, and 8 corners per octagon. Each vertex is where 3 corners coincide, so we count the corners and divide by 3. <math>\text{vertices} = \frac{12 \cdot 4 + 8 \cdot 6 + 6 \cdot 8}{3}=48</math>. | ||
| + | |||
| + | We know that all vertices look the same (from the problem statement), so we should find the number of line segments originating from a vertex, and multiply that by the number of vertices, and divide by 2 (because each space diagonal is counted twice because it has two endpoints). | ||
| + | |||
| + | Counting the vertices that are on the same face as an arbitrary vertex, we find that there are 13 vertices that aren't possible endpoints of a line originating from the vertex in the middle of the diagram. | ||
| + | You can draw a diagram to count this better: [[File:1988AIME10.png]] Since 13 aren't possible endpoints, that means that there are 35 possible endpoints per vertex. | ||
| + | The total number of segments joining vertices that aren't on the same face is <math>48\cdot 35\cdot \frac 12 = 24 \cdot 35 = \boxed{840}</math> | ||
| + | |||
| + | ~breakingbread | ||
| + | |||
| + | == Solution 3 == | ||
| + | |||
| + | Since at each vertex there is one square, one hexagon, and one octagon that meet, then there are a total of <math>12 \cdot 4 = 8 \cdot 6 = 6 \cdot 8 = 48</math> vertices. This means that for each segment we have <math>48</math> choices of vertices for the first endpoint of the segment. | ||
| + | |||
| + | |||
| + | Since each vertex is the meeting point of a square, octagon, and hexagon, then there are <math>3</math> other vertices of the square that are not the first one, and connecting the first point to any of these would result in a segment that lies on a face or edge. | ||
| + | |||
| + | |||
| + | Similarly, there are <math>5</math> points on the adjacent hexagon and <math>7</math> points on adjoining octagon that, when connected to the first point, would result in a diagonal or edge. | ||
| + | |||
| + | |||
| + | However, the square and hexagon share a vertex, as do the square and octagon, and the hexagon and octagon. | ||
| + | |||
| + | |||
| + | Subtracting these from the <math>47</math> vertices we have left to choose from, and adding the <math>3</math> that we counted twice, we get | ||
| + | |||
| + | <cmath>48 \cdot (47 - 3 - 5 - 7 + 3) = 48 \cdot 35 = 1680</cmath> | ||
| + | |||
| + | We over-counted, however, as choosing vertex <math>A</math> then <math>B</math> is the same thing as choosing <math>B</math> then <math>A</math>, so we must divide <math>1680 / 2 = \boxed{840}</math>. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Alternatively, we could have noted from the diagram: | ||
| + | |||
| + | |||
| + | <center> [[File:1988AIME10.png]] </center> | ||
| + | |||
| + | |||
| + | Our first choice would be the vertex in the middle (there are <math>48</math> of these), and our second choice would be any of the remaining 47 points minus the 12 that share a face without chosen vertex. Summing these we get <cmath>48 (47 - 12) = 1680</cmath> And we divide by <math>2</math> as before to get <math>\boxed{840}</math> | ||
| + | |||
| + | == Solution 4 == | ||
| + | |||
| + | In the same ways as above, we find that there are 48 vertices. Now, notice that there are <math>\binom{48}{2}</math> total possible ways to choose two vertices. However, we must remove the cases where the segments do not lie in the interior of the polyhedron. We get | ||
| + | |||
| + | <cmath>\binom{48}{2}-12\binom{4}{2}-8\binom{6}{2}-6\binom{8}{2}=768</cmath> | ||
| + | |||
| + | We remover all the possible edges of the squares, hexagons, and octagons. However, we have undercounted! We must add back the number of edges because when we subtracted the three binomials from <math>\binom{48}{2}</math> we removed each edge twice (each edge is shared by two polygons). This means that we need to add back the number of edges, 72. Thus, we get <math>768+72=\boxed{840}</math>. | ||
| + | |||
| + | == Solution 5 == | ||
| + | We can also use Euler's formula to find the number of vertices. For any polyhedron, it holds that <math>V - E + F = 2</math>. There are <math>12 + 8 + 6 = 26</math> faces. Additionally, the shapes in total have <math>4 \cdot 12 + 6 \cdot 8 + 8 \cdot 6 = 144</math> edges. At an edge of the polyhedron, exactly two of these edges coincide, so we divide by <math>2</math> to get <math>\frac{144}{2} = 72</math>. Plugging in our numbers, we have that <math>V - 72 + 26 = 2</math>. When solved, this gives <math>V = 48</math>. Proceed using any of the methods above. | ||
| + | |||
| + | ~ cxsmi | ||
== See also == | == See also == | ||
| Line 17: | Line 77: | ||
[[Category:Intermediate Combinatorics Problems]] | [[Category:Intermediate Combinatorics Problems]] | ||
| + | {{MAA Notice}} | ||
Latest revision as of 12:25, 19 November 2024
Problem
A convex polyhedron has for its faces 12 squares, 8 regular hexagons, and 6 regular octagons. At each vertex of the polyhedron one square, one hexagon, and one octagon meet. How many segments joining vertices of the polyhedron lie in the interior of the polyhedron rather than along an edge or a face?
Solution 1
The polyhedron described looks like this, a truncated cuboctahedron.
The number of segments joining the vertices of the polyhedron is  . We must now subtract out those segments that lie along an edge or a face.
. We must now subtract out those segments that lie along an edge or a face.
Since every vertex of the polyhedron lies on exactly one vertex of a square/hexagon/octagon, we have that ![]() .
.
Each vertex is formed by the intersection of 3 edges. Since every edge is counted twice, once at each of its endpoints, the number of edges ![]() is
is ![]() .
.
Each of the segments lying on a face of the polyhedron must be a diagonal of that face. Each square contributes ![]() diagonals, each hexagon
diagonals, each hexagon ![]() , and each octagon
, and each octagon ![]() . The number of diagonals is thus
. The number of diagonals is thus ![]() .
.
Subtracting, we get that the number of space diagonals is ![]() .
.
Solution 2
We first find the number of vertices on the polyhedron:
There are 4 corners per square, 6 corners per hexagon, and 8 corners per octagon. Each vertex is where 3 corners coincide, so we count the corners and divide by 3. ![]() .
.
We know that all vertices look the same (from the problem statement), so we should find the number of line segments originating from a vertex, and multiply that by the number of vertices, and divide by 2 (because each space diagonal is counted twice because it has two endpoints).
Counting the vertices that are on the same face as an arbitrary vertex, we find that there are 13 vertices that aren't possible endpoints of a line originating from the vertex in the middle of the diagram.
You can draw a diagram to count this better: 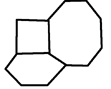 Since 13 aren't possible endpoints, that means that there are 35 possible endpoints per vertex.
The total number of segments joining vertices that aren't on the same face is
Since 13 aren't possible endpoints, that means that there are 35 possible endpoints per vertex.
The total number of segments joining vertices that aren't on the same face is ![]()
~breakingbread
Solution 3
Since at each vertex there is one square, one hexagon, and one octagon that meet, then there are a total of ![]() vertices. This means that for each segment we have
vertices. This means that for each segment we have ![]() choices of vertices for the first endpoint of the segment.
choices of vertices for the first endpoint of the segment.
Since each vertex is the meeting point of a square, octagon, and hexagon, then there are ![]() other vertices of the square that are not the first one, and connecting the first point to any of these would result in a segment that lies on a face or edge.
other vertices of the square that are not the first one, and connecting the first point to any of these would result in a segment that lies on a face or edge.
Similarly, there are ![]() points on the adjacent hexagon and
points on the adjacent hexagon and ![]() points on adjoining octagon that, when connected to the first point, would result in a diagonal or edge.
points on adjoining octagon that, when connected to the first point, would result in a diagonal or edge.
However, the square and hexagon share a vertex, as do the square and octagon, and the hexagon and octagon.
Subtracting these from the ![]() vertices we have left to choose from, and adding the
vertices we have left to choose from, and adding the ![]() that we counted twice, we get
that we counted twice, we get
![]()
We over-counted, however, as choosing vertex ![]() then
then ![]() is the same thing as choosing
is the same thing as choosing ![]() then
then ![]() , so we must divide
, so we must divide ![]() .
.
Alternatively, we could have noted from the diagram:

Our first choice would be the vertex in the middle (there are ![]() of these), and our second choice would be any of the remaining 47 points minus the 12 that share a face without chosen vertex. Summing these we get
of these), and our second choice would be any of the remaining 47 points minus the 12 that share a face without chosen vertex. Summing these we get ![]() And we divide by
And we divide by ![]() as before to get
as before to get ![]()
Solution 4
In the same ways as above, we find that there are 48 vertices. Now, notice that there are ![]() total possible ways to choose two vertices. However, we must remove the cases where the segments do not lie in the interior of the polyhedron. We get
total possible ways to choose two vertices. However, we must remove the cases where the segments do not lie in the interior of the polyhedron. We get
![\[\binom{48}{2}-12\binom{4}{2}-8\binom{6}{2}-6\binom{8}{2}=768\]](http://latex.artofproblemsolving.com/f/d/b/fdb6be40d92783a1397bf7fe61473d7ef939c903.png)
We remover all the possible edges of the squares, hexagons, and octagons. However, we have undercounted! We must add back the number of edges because when we subtracted the three binomials from ![]() we removed each edge twice (each edge is shared by two polygons). This means that we need to add back the number of edges, 72. Thus, we get
we removed each edge twice (each edge is shared by two polygons). This means that we need to add back the number of edges, 72. Thus, we get ![]() .
.
Solution 5
We can also use Euler's formula to find the number of vertices. For any polyhedron, it holds that ![]() . There are
. There are ![]() faces. Additionally, the shapes in total have
faces. Additionally, the shapes in total have ![]() edges. At an edge of the polyhedron, exactly two of these edges coincide, so we divide by
edges. At an edge of the polyhedron, exactly two of these edges coincide, so we divide by ![]() to get
to get ![]() . Plugging in our numbers, we have that
. Plugging in our numbers, we have that ![]() . When solved, this gives
. When solved, this gives ![]() . Proceed using any of the methods above.
. Proceed using any of the methods above.
~ cxsmi
See also
| 1988 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 9 |
Followed by Problem 11 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.