Difference between revisions of "2024 AMC 10A Problems/Problem 12"
(→See Also) |
(→Solution) |
||
| Line 5: | Line 5: | ||
==Solution== | ==Solution== | ||
| − | + | Going through the table, we see her scores over the six days were: <math>1700</math>, <math>1700+80=1780</math>, <math>1780-90=1690</math>, <math>1690-10=1680</math>, <math>1680+60=1740</math>, and <math>1740-40=1700</math>. | |
| + | Taking the average, we get <math>\frac{(1700+1780+1690+1680+1740+1700)}{6} = \boxed{\textbf{(E) } 1715}.</math> | ||
| + | |||
| + | -i_am_suk_at_math_2 | ||
==See Also== | ==See Also== | ||
{{AMC10 box|year=2024|ab=A|num-b=10|num-a=12}} | {{AMC10 box|year=2024|ab=A|num-b=10|num-a=12}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 17:02, 8 November 2024
Problem
Zelda played the Adventures of Math game on August 1 and scored ![]() points. She continued to play daily over the next
points. She continued to play daily over the next ![]() days. The bar chart below shows the daily change in her score compared to the day before. (For example, Zelda's score on August 2 was
days. The bar chart below shows the daily change in her score compared to the day before. (For example, Zelda's score on August 2 was ![]() points.) What was Zelda's average score in points over the
points.) What was Zelda's average score in points over the ![]() days?
days?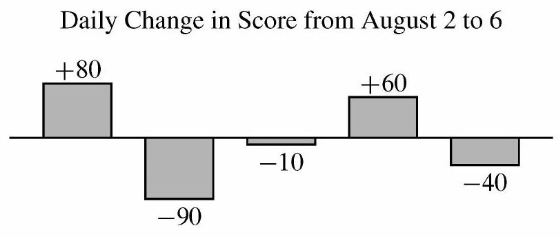
![]()
Solution
Going through the table, we see her scores over the six days were: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
Taking the average, we get
.
Taking the average, we get ![]()
-i_am_suk_at_math_2
See Also
| 2024 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 10 |
Followed by Problem 12 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 









