Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2014 AIME II Problems/Problem 14"
 
(40 intermediate revisions by 16 users not shown)
Line 1: Line 1:
−
14. In △ABC, AB=10, ∠A=30∘, and ∠C=45∘. Let H, D, and M be points on the line BC such that AH⊥BC, ∠BAD=∠CAD, and <math>BM=CM</math>. Point <math>N</math> is the midpoint of the segment <math>HM</math>, and point <math>P</math> is on ray <math>AD</math> such that PN⊥BC. Then <math>AP^2=\dfrac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>.
+
==Problem==
 +
In <math>\triangle{ABC}, AB=10, \angle{A}=30^\circ</math> , and <math>\angle{C=45^\circ}</math>. Let <math>H, D,</math> and <math>M</math> be points on the line <math>BC</math> such that <math>AH\perp{BC}</math>, <math>\angle{BAD}=\angle{CAD}</math>, and <math>BM=CM</math>. Point <math>N</math> is the midpoint of the segment <math>HM</math>, and point <math>P</math> is on ray <math>AD</math> such that <math>PN\perp{BC}</math>. Then <math>AP^2=\dfrac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>.
  
−
http://www.artofproblemsolving.com/Wiki/images/5/59/AOPS_wiki.PNG ( This is the diagram.)
+
==Diagram==
−
+
<asy>
 +
unitsize(20);
 +
pair A = MP("A",(-5sqrt(3),0)), B = MP("B",(0,5),N), C = MP("C",(5,0)), M = D(MP("M",0.5(B+C),NE)), D = MP("D",IP(L(A,incenter(A,B,C),0,2),B--C),N), H = MP("H",foot(A,B,C),N), N = MP("N",0.5(H+M),NE), P = MP("P",IP(A--D,L(N,N-(1,1),0,10)));
 +
D(A--B--C--cycle);
 +
D(B--H--A,blue+dashed);
 +
D(A--D);
 +
D(P--N);
 +
markscalefactor = 0.05;
 +
D(rightanglemark(A,H,B));
 +
D(rightanglemark(P,N,D));
 +
MP("10",0.5(A+B)-(-0.1,0.1),NW);
 +
</asy>
 +
 
 +
==Solution 1==
 +
 
 +
Let us just drop the perpendicular from <math>B</math> to <math>AC</math> and label the point of intersection <math>O</math>. We will use this point later in the problem.
 
As we can see,  
 
As we can see,  
 +
<math>M</math> is the midpoint of <math>BC</math> and <math>N</math> is the midpoint of <math>HM</math>
 +
<math>AHC</math> is a <math>45-45-90</math> triangle, so <math>\angle{HAB}=15^\circ</math>.
 +
<math>AHD</math> is <math>30-60-90</math> triangle.
 +
 +
<math>AH</math> and <math>PN</math> are parallel lines so <math>PND</math> is <math>30-60-90</math> triangle also.
 +
Then if we use those informations we get <math>AD=2HD</math> and <math>PD=2ND</math> and <math>AP=AD-PD=2HD-2ND=2HN</math> or <math>AP=2HN=HM</math>.
 +
Now we know  that <math>HM=AP</math>, we can find for <math>HM</math> which is simpler to find.
 +
We can use point <math>B</math> to split it up as <math>HM=HB+BM</math>,
 +
We can chase those lengths and we would get <math>AB=10</math>, so <math>OB=5</math>, so <math>BC=5\sqrt{2}</math>, so <math>BM=\dfrac{1}{2} \cdot BC=\dfrac{5\sqrt{2}}{2}</math>
 +
We can also use Law of Sines:
 +
<cmath>\frac{BC}{AB}=\frac{\sin\angle A}{\sin\angle C}</cmath>
 +
<cmath>\frac{BC}{10}=\frac{\frac{1}{2}}{\frac{\sqrt{2}}{2}}\implies BC=5\sqrt{2}</cmath>
 +
Then using right triangle <math>AHB</math>, we have <math>HB=10 \sin 15^\circ</math>
 +
So <math>HB=10 \sin 15^\circ=\dfrac{5(\sqrt{6}-\sqrt{2})}{2}</math>.
 +
And we know that <math>AP = HM = HB + BM = \frac{5(\sqrt6-\sqrt2)}{2} + \frac{5\sqrt2}{2} = \frac{5\sqrt6}{2}</math>.
 +
Finally if we calculate <math>(AP)^2</math>.
 +
<math>(AP)^2=\dfrac{150}{4}=\dfrac{75}{2}</math>. So our final answer is <math>75+2=77</math>.
 +
<math>m+n=\boxed{077}</math>
  
−
<math>M</math> is the midpoint of <math>BC</math> and <math>N</math> is the midpoint of <math>HM</math>
+
-Gamjawon
 +
-edited by srisainandan6 to clarify and correct a small mistake
 +
 
 +
==Solution 2==
 +
Here's a solution that doesn't need <math>\sin 15^\circ</math>.
 +
 
 +
As above, get to <math>AP=HM</math>.  As in the figure, let <math>O</math> be the foot of the perpendicular from <math>B</math> to <math>AC</math>.  Then <math>BCO</math> is a 45-45-90 triangle, and <math>ABO</math> is a 30-60-90 triangle.  So <math>BO=5</math> and <math>AO=5\sqrt{3}</math>; also, <math>CO=5</math>, <math>BC=5\sqrt2</math>, and <math>MC=\dfrac{BC}{2}=5\dfrac{\sqrt2}{2}</math>.  But <math>MO</math> and <math>AH</math> are parallel, both being orthogonal to <math>BC</math>.  Therefore <math>MH:AO=MC:CO</math>, or <math>MH=\dfrac{5\sqrt3}{\sqrt2}</math>, and we're done.
  
−
<math>AHC</math> is a <math>45-45-90</math> triangle, so ∠HAB=15∘.
+
==Solution 3==
 +
Break our diagram into 2 special right triangle by dropping an altitude from <math>B</math> to <math>AC</math> we then get that <cmath>AC=5+5\sqrt{3}, BC=5\sqrt{2}.</cmath>
 +
Since <math>\triangle{HCA}</math> is a 45-45-90,
  
−
<math>AHD</math> is <math>30-60-90</math>.
+
<cmath>HC=\frac{5\sqrt2+5\sqrt6}{2}</cmath>
 +
<math>MC=\frac{BC}{2},</math>  
 +
<cmath>HM=\frac{5\sqrt6}{2}</cmath>
 +
<cmath>HN=\frac{5\sqrt6}{4}</cmath>
 +
We know that <math>\triangle{AHD}\simeq \triangle{PND}</math> and are 30-60-90. 
 +
Thus, <cmath>AP=2 \cdot HN=\frac{5\sqrt6}{2}.</cmath>
  
−
<math>AH</math> and <math>PN</math> are parallel lines so <math>PND</math> is <math>30-60-90</math> also.
+
<math>(AP)^2=\dfrac{150}{4}=\dfrac{75}{2}</math>. So our final answer is <math>75+2=\boxed{077}</math>.
  
−
Then if we use those informations we get <math>AD=2HD</math> and
+
==Solution 4==
 +
<asy>
 +
/* Geogebra to Asymptote conversion, documentation at artofproblemsolving.com/Wiki go to User:Azjps/geogebra */
 +
import graph; size(15cm);
 +
real labelscalefactor = 0.5; /* changes label-to-point distance */
 +
pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */
 +
pen dotstyle = black; /* point style */
 +
real xmin = -8.455641974276588, xmax = 26.731282460265, ymin = -10.92318356252699, ymax = 9.023689834456471;  /* image dimensions */
 +
pen wrwrwr = rgb(0.3803921568627451,0.3803921568627451,0.3803921568627451); pen rvwvcq = rgb(0.08235294117647059,0.396078431372549,0.7529411764705882);
  
−
<math>PD=2ND</math> and <math>AP=AD-PD=2HD-2ND=2HN</math> or <math>AP=2HN=HM</math>
+
draw((-1.4934334172297545,2.6953043701763835)--(-1.459546107520503,-6.96389444957376)--(1.1286284157632023,-6.954814372303504)--(4.651736947776926,-3.406898607850789)--(4.642656870506668,-0.8187240845670819)--cycle, linewidth(2) + rvwvcq);
 +
/* draw figures */
 +
draw((-1.4934334172297545,2.6953043701763835)--(1.1286284157632023,-6.954814372303504), linewidth(2) + wrwrwr);
 +
draw((xmin, -0.9930079421029264*xmin + 1.2123131258653241)--(xmax, -0.9930079421029264*xmax + 1.2123131258653241), linewidth(2) + wrwrwr); /* line */
 +
draw((xmin, 0.0035082940460819836*xmin-6.958773932654766)--(xmax, 0.0035082940460819836*xmax-6.958773932654766), linewidth(2) + wrwrwr); /* line */
 +
draw((xmin, -285.03882139434313*xmin-422.9911967079192)--(xmax, -285.03882139434313*xmax-422.9911967079192), linewidth(2) + wrwrwr); /* line */
 +
draw((xmin, -1.7181023895538718*xmin + 0.12943284739433739)--(xmax, -1.7181023895538718*xmax + 0.12943284739433739), linewidth(2) + wrwrwr); /* line */
 +
draw(circle((4.642656870506668,-0.8187240845670819), 7.071067811865476), linewidth(2) + wrwrwr);
 +
draw((xmin, -285.0388213943529*xmin + 1322.5187184230485)--(xmax, -285.0388213943529*xmax + 1322.5187184230485), linewidth(2) + wrwrwr); /* line */
 +
draw((-1.4934334172297545,2.6953043701763835)--(4.617849638067675,6.252300211899359), linewidth(2) + wrwrwr);
 +
draw((4.617849638067675,6.252300211899359)--(-1.459546107520503,-6.96389444957376), linewidth(2) + wrwrwr);
 +
draw(circle((-0.18240250073327363,-2.12975500106356), 5), linewidth(2) + wrwrwr);
 +
draw((xmin, -285.0388213943432*xmin + 449.7637608575419)--(xmax, -285.0388213943432*xmax + 449.7637608575419), linewidth(2) + wrwrwr); /* line */
 +
draw((1.1286284157632023,-6.954814372303504)--(4.651736947776926,-3.406898607850789), linewidth(2) + wrwrwr);
 +
draw((-1.4934334172297545,2.6953043701763835)--(4.642656870506668,-0.8187240845670819), linewidth(2) + wrwrwr);
 +
draw((-1.4934334172297545,2.6953043701763835)--(-1.459546107520503,-6.96389444957376), linewidth(2) + rvwvcq);
 +
draw((-1.459546107520503,-6.96389444957376)--(1.1286284157632023,-6.954814372303504), linewidth(2) + rvwvcq);
 +
draw((1.1286284157632023,-6.954814372303504)--(4.651736947776926,-3.406898607850789), linewidth(2) + rvwvcq);
 +
draw((4.651736947776926,-3.406898607850789)--(4.642656870506668,-0.8187240845670819), linewidth(2) + rvwvcq);
 +
draw((4.642656870506668,-0.8187240845670819)--(-1.4934334172297545,2.6953043701763835), linewidth(2) + rvwvcq);
 +
/* dots and labels */
 +
dot((-1.4934334172297545,2.6953043701763835),dotstyle);
 +
label("$A$", (-1.3954084351380491,2.9230996889873015), NE * labelscalefactor);
 +
dot((1.1286284157632023,-6.954814372303504),dotstyle);
 +
label("$B$", (1.2093379191072373,-6.719031552166216), NE * labelscalefactor);
 +
dot((8.199652712229643,-6.930007139864511),linewidth(4pt) + dotstyle);
 +
label("$C$", (8.292420110475998,-6.741880204396438), NE * labelscalefactor);
 +
dot((-1.459546107520503,-6.96389444957376),linewidth(4pt) + dotstyle);
 +
label("$H$", (-1.3725597829078273,-6.787577508856881), NE * labelscalefactor);
 +
dot((-1.4686261847907602,-4.375719926290057),linewidth(4pt) + dotstyle);
 +
label("$E$", (-1.3725597829078273,-4.182831154611618), NE * labelscalefactor);
 +
dot((4.617849638067675,6.252300211899359),linewidth(4pt) + dotstyle);
 +
label("$L$", (4.705181710331174,6.441792132441429), NE * labelscalefactor);
 +
dot((4.642656870506668,-0.8187240845670819),linewidth(4pt) + dotstyle);
 +
label("$O$", (4.728030362561396,-0.6412900589272691), NE * labelscalefactor);
 +
dot((4.117194931218359,-6.944329602191013),linewidth(4pt) + dotstyle);
 +
label("$D$", (4.2025113612662945,-6.764728856626659), NE * labelscalefactor);
 +
dot((4.6674641029456625,-7.889748381033524),linewidth(4pt) + dotstyle);
 +
label("$F$", (4.750879014791618,-7.701523598065745), NE * labelscalefactor);
 +
dot((4.651736947776926,-3.406898607850789),linewidth(4pt) + dotstyle);
 +
label("$G$", (4.750879014791618,-3.2231877609423107), NE * labelscalefactor);
 +
dot((1.5791517652735851,-0.3557971188372022),linewidth(4pt) + dotstyle);
 +
label("$K$", (1.6663109637116735,-0.18431701432283698), NE * labelscalefactor);
 +
dot((1.5870153428579534,-2.5972220054285695),linewidth(4pt) + dotstyle);
 +
label("$P$", (1.6891596159418953,-2.4234849328845542), NE * labelscalefactor);
 +
clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle);
 +
/* end of picture */
 +
</asy>
 +
Draw the <math>45-45-90 \triangle AHC</math>. Now, take the perpendicular bisector of <math>BC</math> to intersect the circumcircle of <math>\triangle ABC</math> and <math>AC</math> at <math>F, L, G</math> as shown, and denote <math>O</math> to be the circumcenter of <math>\triangle ABC</math>. It is not difficult to see by angle chasing that <math>AHBGO</math> is cyclic, namely with diameter <math>AB</math>. Then, by symmetry, <math>EH = HB</math> and as <math>HB, OG</math> are both subtended by equal arcs they are equal. Hence, <math>EH = GO</math>. Now, draw line <math>HL</math> and intersect it at <math>AC</math> at point <math>K</math> in the diagram. It is not hard to use angle chase to arrive at <math>AEOL</math> a parallelogram, and from our length condition derived earlier, <math>AL \parallel HG</math>. From here, it is clear that <math>AK = KG</math>; that is, <math>P</math> is just the intersection of the perpendicular from <math>K</math> down to <math>BC</math> and <math>AD</math>! After this point, note that <math>AP = PF</math>. It is easily derived that the circumradius of <math>\triangle ABC</math> is <math>\frac{10}{\sqrt{2}}</math>. Now, <math>APO</math> is a <math>30-60-90</math> triangle, and from here it is easy to arrive at the final answer of <math>\boxed{077}</math>. ~awang11's sol
  
−
Now we know that HM=AP, we can find for HM which is simpler to find.
+
==Solution 5==
 +
[[File:2014 AIME II 14.png|500px|right]]
 +
Let <math>BO \perp AC, O \in AC.</math>
 +
   
 +
Let <math>ME \perp BC, E \in AD.</math>
  
−
We can use point B to split it up as HM=HB+BM,
+
<math>MB = MC, \angle C = 45^\circ \implies</math> points <math>M, E, O</math> are collinear.
  
−
We can chase those lengths and we would get
+
<math>HN = NM, AH||NP||ME \implies AP = PE.</math>
  
−
<math>AB=10</math>, so <math>OB=5</math>, so <math>BC=5\sqrt{2}</math>, so <math>BM=\dfrac{1}{2} \cdot BC=\dfrac{5\sqrt{2}}{2}</math>
+
In <math>\triangle ABO \hspace{10mm} \angle A = 30^\circ \implies AO = AB \cos 60^\circ  = 5 \sqrt{3}.</math>
  
−
Then using right triangle <math>AHB</math>, we have HB=10 sin (15∘)
+
In <math>\triangle AEO \hspace{10mm} \angle A = 15^\circ, \angle O = 90^\circ + 45^\circ = 135^\circ  \implies</math>
 +
<cmath>\angle AEO = 30^\circ \implies</cmath>
 +
<cmath>AE = AO \frac {\sin 135^\circ}{\sin 30^\circ}  = 5 \sqrt{3} \cdot \sqrt{2} = 5 \sqrt{6} \implies</cmath>
 +
<cmath>AP = 5 \sqrt {\frac {3}{2}} \implies AP^2 = \frac {75}{2} \implies  \boxed{\textbf{077}}.</cmath>
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
  
−
So HB=10 sin (15∘)=<math>\dfrac{5(\sqrt{6}-\sqrt{2})}{2}</math>.
 
  
−
And we know that <math>AP = HM = HB + BM = \frac{5(\sqrt6-\sqrt2)}{2} + \frac{5\sqrt2}{2} = \frac{5\sqrt6}{2}</math>.
+
==Video solution==
  
−
Finally if we calculate <math>(AP)^2</math>.
+
https://www.youtube.com/watch?v=SvJ0wDJphdU
  
−
<math>(AP)^2=\dfrac{150}{4}=\dfrac{75}{2}</math>. So our final answer is <math>75+2=77</math>.
+
== See also ==
 +
{{AIME box|year=2014|n=II|num-b=13|num-a=15}}
  
−
<math>m+n=\boxed{77}</math>
+
[[Category:Intermediate Geometry Problems]]
 +
{{MAA Notice}}

Latest revision as of 19:40, 24 October 2024

Problem

In $\triangle{ABC}, AB=10, \angle{A}=30^\circ$ , and $\angle{C=45^\circ}$. Let $H, D,$ and $M$ be points on the line $BC$ such that $AH\perp{BC}$, $\angle{BAD}=\angle{CAD}$, and $BM=CM$. Point $N$ is the midpoint of the segment $HM$, and point $P$ is on ray $AD$ such that $PN\perp{BC}$. Then $AP^2=\dfrac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.

Diagram

[asy] unitsize(20); pair A = MP("A",(-5sqrt(3),0)), B = MP("B",(0,5),N), C = MP("C",(5,0)), M = D(MP("M",0.5(B+C),NE)), D = MP("D",IP(L(A,incenter(A,B,C),0,2),B--C),N), H = MP("H",foot(A,B,C),N), N = MP("N",0.5(H+M),NE), P = MP("P",IP(A--D,L(N,N-(1,1),0,10))); D(A--B--C--cycle); D(B--H--A,blue+dashed); D(A--D); D(P--N); markscalefactor = 0.05; D(rightanglemark(A,H,B)); D(rightanglemark(P,N,D)); MP("10",0.5(A+B)-(-0.1,0.1),NW); [/asy]

Solution 1

Let us just drop the perpendicular from $B$ to $AC$ and label the point of intersection $O$. We will use this point later in the problem. As we can see, $M$ is the midpoint of $BC$ and $N$ is the midpoint of $HM$ $AHC$ is a $45-45-90$ triangle, so $\angle{HAB}=15^\circ$. $AHD$ is $30-60-90$ triangle.

$AH$ and $PN$ are parallel lines so $PND$ is $30-60-90$ triangle also. Then if we use those informations we get $AD=2HD$ and $PD=2ND$ and $AP=AD-PD=2HD-2ND=2HN$ or $AP=2HN=HM$. Now we know that $HM=AP$, we can find for $HM$ which is simpler to find. We can use point $B$ to split it up as $HM=HB+BM$, We can chase those lengths and we would get $AB=10$, so $OB=5$, so $BC=5\sqrt{2}$, so $BM=\dfrac{1}{2} \cdot BC=\dfrac{5\sqrt{2}}{2}$ We can also use Law of Sines: \[\frac{BC}{AB}=\frac{\sin\angle A}{\sin\angle C}\] \[\frac{BC}{10}=\frac{\frac{1}{2}}{\frac{\sqrt{2}}{2}}\implies BC=5\sqrt{2}\] Then using right triangle $AHB$, we have $HB=10 \sin 15^\circ$ So $HB=10 \sin 15^\circ=\dfrac{5(\sqrt{6}-\sqrt{2})}{2}$. And we know that $AP = HM = HB + BM = \frac{5(\sqrt6-\sqrt2)}{2} + \frac{5\sqrt2}{2} = \frac{5\sqrt6}{2}$. Finally if we calculate $(AP)^2$. $(AP)^2=\dfrac{150}{4}=\dfrac{75}{2}$. So our final answer is $75+2=77$. $m+n=\boxed{077}$

-Gamjawon -edited by srisainandan6 to clarify and correct a small mistake

Solution 2

Here's a solution that doesn't need $\sin 15^\circ$.

As above, get to $AP=HM$. As in the figure, let $O$ be the foot of the perpendicular from $B$ to $AC$. Then $BCO$ is a 45-45-90 triangle, and $ABO$ is a 30-60-90 triangle. So $BO=5$ and $AO=5\sqrt{3}$; also, $CO=5$, $BC=5\sqrt2$, and $MC=\dfrac{BC}{2}=5\dfrac{\sqrt2}{2}$. But $MO$ and $AH$ are parallel, both being orthogonal to $BC$. Therefore $MH:AO=MC:CO$, or $MH=\dfrac{5\sqrt3}{\sqrt2}$, and we're done.

Solution 3

Break our diagram into 2 special right triangle by dropping an altitude from $B$ to $AC$ we then get that \[AC=5+5\sqrt{3}, BC=5\sqrt{2}.\] Since $\triangle{HCA}$ is a 45-45-90,

\[HC=\frac{5\sqrt2+5\sqrt6}{2}\] $MC=\frac{BC}{2},$ \[HM=\frac{5\sqrt6}{2}\] \[HN=\frac{5\sqrt6}{4}\] We know that $\triangle{AHD}\simeq \triangle{PND}$ and are 30-60-90. Thus, \[AP=2 \cdot HN=\frac{5\sqrt6}{2}.\]

$(AP)^2=\dfrac{150}{4}=\dfrac{75}{2}$. So our final answer is $75+2=\boxed{077}$.

Solution 4

[asy] /* Geogebra to Asymptote conversion, documentation at artofproblemsolving.com/Wiki go to User:Azjps/geogebra */ import graph; size(15cm); real labelscalefactor = 0.5; /* changes label-to-point distance */ pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ pen dotstyle = black; /* point style */ real xmin = -8.455641974276588, xmax = 26.731282460265, ymin = -10.92318356252699, ymax = 9.023689834456471; /* image dimensions */ pen wrwrwr = rgb(0.3803921568627451,0.3803921568627451,0.3803921568627451); pen rvwvcq = rgb(0.08235294117647059,0.396078431372549,0.7529411764705882); draw((-1.4934334172297545,2.6953043701763835)--(-1.459546107520503,-6.96389444957376)--(1.1286284157632023,-6.954814372303504)--(4.651736947776926,-3.406898607850789)--(4.642656870506668,-0.8187240845670819)--cycle, linewidth(2) + rvwvcq); /* draw figures */ draw((-1.4934334172297545,2.6953043701763835)--(1.1286284157632023,-6.954814372303504), linewidth(2) + wrwrwr); draw((xmin, -0.9930079421029264*xmin + 1.2123131258653241)--(xmax, -0.9930079421029264*xmax + 1.2123131258653241), linewidth(2) + wrwrwr); /* line */ draw((xmin, 0.0035082940460819836*xmin-6.958773932654766)--(xmax, 0.0035082940460819836*xmax-6.958773932654766), linewidth(2) + wrwrwr); /* line */ draw((xmin, -285.03882139434313*xmin-422.9911967079192)--(xmax, -285.03882139434313*xmax-422.9911967079192), linewidth(2) + wrwrwr); /* line */ draw((xmin, -1.7181023895538718*xmin + 0.12943284739433739)--(xmax, -1.7181023895538718*xmax + 0.12943284739433739), linewidth(2) + wrwrwr); /* line */ draw(circle((4.642656870506668,-0.8187240845670819), 7.071067811865476), linewidth(2) + wrwrwr); draw((xmin, -285.0388213943529*xmin + 1322.5187184230485)--(xmax, -285.0388213943529*xmax + 1322.5187184230485), linewidth(2) + wrwrwr); /* line */ draw((-1.4934334172297545,2.6953043701763835)--(4.617849638067675,6.252300211899359), linewidth(2) + wrwrwr); draw((4.617849638067675,6.252300211899359)--(-1.459546107520503,-6.96389444957376), linewidth(2) + wrwrwr); draw(circle((-0.18240250073327363,-2.12975500106356), 5), linewidth(2) + wrwrwr); draw((xmin, -285.0388213943432*xmin + 449.7637608575419)--(xmax, -285.0388213943432*xmax + 449.7637608575419), linewidth(2) + wrwrwr); /* line */ draw((1.1286284157632023,-6.954814372303504)--(4.651736947776926,-3.406898607850789), linewidth(2) + wrwrwr); draw((-1.4934334172297545,2.6953043701763835)--(4.642656870506668,-0.8187240845670819), linewidth(2) + wrwrwr); draw((-1.4934334172297545,2.6953043701763835)--(-1.459546107520503,-6.96389444957376), linewidth(2) + rvwvcq); draw((-1.459546107520503,-6.96389444957376)--(1.1286284157632023,-6.954814372303504), linewidth(2) + rvwvcq); draw((1.1286284157632023,-6.954814372303504)--(4.651736947776926,-3.406898607850789), linewidth(2) + rvwvcq); draw((4.651736947776926,-3.406898607850789)--(4.642656870506668,-0.8187240845670819), linewidth(2) + rvwvcq); draw((4.642656870506668,-0.8187240845670819)--(-1.4934334172297545,2.6953043701763835), linewidth(2) + rvwvcq); /* dots and labels */ dot((-1.4934334172297545,2.6953043701763835),dotstyle); label("$A$", (-1.3954084351380491,2.9230996889873015), NE * labelscalefactor); dot((1.1286284157632023,-6.954814372303504),dotstyle); label("$B$", (1.2093379191072373,-6.719031552166216), NE * labelscalefactor); dot((8.199652712229643,-6.930007139864511),linewidth(4pt) + dotstyle); label("$C$", (8.292420110475998,-6.741880204396438), NE * labelscalefactor); dot((-1.459546107520503,-6.96389444957376),linewidth(4pt) + dotstyle); label("$H$", (-1.3725597829078273,-6.787577508856881), NE * labelscalefactor); dot((-1.4686261847907602,-4.375719926290057),linewidth(4pt) + dotstyle); label("$E$", (-1.3725597829078273,-4.182831154611618), NE * labelscalefactor); dot((4.617849638067675,6.252300211899359),linewidth(4pt) + dotstyle); label("$L$", (4.705181710331174,6.441792132441429), NE * labelscalefactor); dot((4.642656870506668,-0.8187240845670819),linewidth(4pt) + dotstyle); label("$O$", (4.728030362561396,-0.6412900589272691), NE * labelscalefactor); dot((4.117194931218359,-6.944329602191013),linewidth(4pt) + dotstyle); label("$D$", (4.2025113612662945,-6.764728856626659), NE * labelscalefactor); dot((4.6674641029456625,-7.889748381033524),linewidth(4pt) + dotstyle); label("$F$", (4.750879014791618,-7.701523598065745), NE * labelscalefactor); dot((4.651736947776926,-3.406898607850789),linewidth(4pt) + dotstyle); label("$G$", (4.750879014791618,-3.2231877609423107), NE * labelscalefactor); dot((1.5791517652735851,-0.3557971188372022),linewidth(4pt) + dotstyle); label("$K$", (1.6663109637116735,-0.18431701432283698), NE * labelscalefactor); dot((1.5870153428579534,-2.5972220054285695),linewidth(4pt) + dotstyle); label("$P$", (1.6891596159418953,-2.4234849328845542), NE * labelscalefactor); clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle); /* end of picture */ [/asy] Draw the $45-45-90 \triangle AHC$. Now, take the perpendicular bisector of $BC$ to intersect the circumcircle of $\triangle ABC$ and $AC$ at $F, L, G$ as shown, and denote $O$ to be the circumcenter of $\triangle ABC$. It is not difficult to see by angle chasing that $AHBGO$ is cyclic, namely with diameter $AB$. Then, by symmetry, $EH = HB$ and as $HB, OG$ are both subtended by equal arcs they are equal. Hence, $EH = GO$. Now, draw line $HL$ and intersect it at $AC$ at point $K$ in the diagram. It is not hard to use angle chase to arrive at $AEOL$ a parallelogram, and from our length condition derived earlier, $AL \parallel HG$. From here, it is clear that $AK = KG$; that is, $P$ is just the intersection of the perpendicular from $K$ down to $BC$ and $AD$! After this point, note that $AP = PF$. It is easily derived that the circumradius of $\triangle ABC$ is $\frac{10}{\sqrt{2}}$. Now, $APO$ is a $30-60-90$ triangle, and from here it is easy to arrive at the final answer of $\boxed{077}$. ~awang11's sol

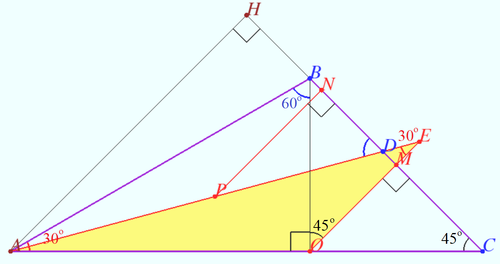
Solution 5

2014 AIME II 14.png

Let $BO \perp AC, O \in AC.$

Let $ME \perp BC, E \in AD.$

$MB = MC, \angle C = 45^\circ \implies$ points $M, E, O$ are collinear.

$HN = NM, AH||NP||ME \implies AP = PE.$

In $\triangle ABO \hspace{10mm} \angle A = 30^\circ \implies AO = AB \cos 60^\circ = 5 \sqrt{3}.$

In $\triangle AEO \hspace{10mm} \angle A = 15^\circ, \angle O = 90^\circ + 45^\circ = 135^\circ \implies$ \[\angle AEO = 30^\circ \implies\] \[AE = AO \frac {\sin 135^\circ}{\sin 30^\circ} = 5 \sqrt{3} \cdot \sqrt{2} = 5 \sqrt{6} \implies\] \[AP = 5 \sqrt {\frac {3}{2}} \implies AP^2 = \frac {75}{2} \implies \boxed{\textbf{077}}.\] vladimir.shelomovskii@gmail.com, vvsss


Video solution

https://www.youtube.com/watch?v=SvJ0wDJphdU

See also

2014 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 13 		Followed by
Problem 15
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2014_AIME_II_Problems/Problem_14&oldid=230562"