Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Miquel's point"

(Created page with "==Miquel and Steiner's quadrilateral theorem== 500px|right Let four lines made four triangles of a complete quadrilateral. In the diagram these are <math>\t...")
 
(→‎Analogue of Miquel's point)
 
(10 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
==Miquel and Steiner's quadrilateral theorem==
 
==Miquel and Steiner's quadrilateral theorem==
−
[[Miquel circles|500px|right]]
+
[[File:4 Miquel circles.png|500px|right]]
 
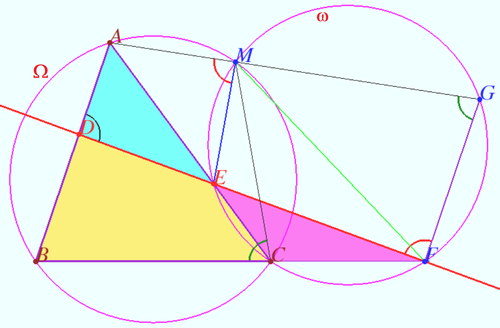
Let four lines made four triangles of a complete quadrilateral. In the diagram these are <math>\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.</math>
 
Let four lines made four triangles of a complete quadrilateral. In the diagram these are <math>\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.</math>
  
Line 7: Line 7:
 
<i><b>Proof</b></i>
 
<i><b>Proof</b></i>
  
−
Let circumcircle of <math>\triangle ABC</math> circle <math>\Omega</math> cross the circumcircle of <math>\triangle CEF \omega</math> at point <math>M.</math>
+
Let circumcircle of <math>\triangle ABC</math> circle <math>\Omega</math> cross the circumcircle of <math>\triangle CEF</math> circle <math>\omega</math> at point <math>M.</math>
  
 
Let <math>AM</math> cross <math>\omega</math> second time in the point <math>G.</math>
 
Let <math>AM</math> cross <math>\omega</math> second time in the point <math>G.</math>
Line 13: Line 13:
 
<math>CMGF</math> is cyclic <math>\implies \angle BCM = \angle MGF.</math>
 
<math>CMGF</math> is cyclic <math>\implies \angle BCM = \angle MGF.</math>
  
−
<math>AMCB</math> is cyclic <math>\implies \angle BCM + \angle BAM = 180^\circ \implies \angle BAG + \angle AGF = 180^\circ \implies AB||GF.</math>
+
<math>AMCB</math> is cyclic <math>\implies \angle BCM + \angle BAM = 180^\circ \implies</math>
 +
 
 +
<math>\angle BAG + \angle AGF = 180^\circ \implies AB||GF.</math>
  
 
<math>CMGF</math> is cyclic <math>\implies \angle AME = \angle EFG.</math>
 
<math>CMGF</math> is cyclic <math>\implies \angle AME = \angle EFG.</math>
  
−
<math>AD||GF \implies \angle ADE + \angle DFG = 180^\circ \implies \angle ADE + \angle AME = 180^\circ \implies ADEM</math> is cyclic and circumcircle of <math>\triangle ADE</math> contain the point <math>M.</math>
+
<math>AD||GF \implies \angle ADE + \angle DFG = 180^\circ \implies \angle ADE + \angle AME = 180^\circ \implies</math>
 +
 
 +
<math>ADEM</math> is cyclic and circumcircle of <math>\triangle ADE</math> contain the point <math>M.</math>
  
 
Similarly circumcircle of <math>\triangle BDF</math> contain the point <math>M</math> as desired.
 
Similarly circumcircle of <math>\triangle BDF</math> contain the point <math>M</math> as desired.
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 +
==Circle of circumcenters==
 +
[[File:Miquel point.png|450px|right]]
 +
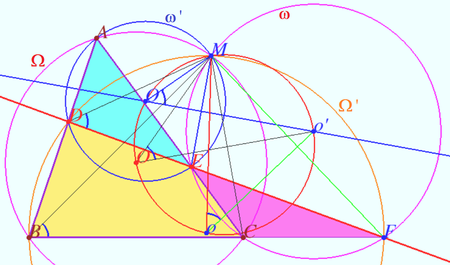
Let four lines made four triangles of a complete quadrilateral. In the diagram these are <math>\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.</math>
 +
 +
Prove that the circumcenters of all four triangles and point <math>M</math> are concyclic.
 +
 +
<i><b>Proof</b></i>
 +
 +
Let <math>\Omega, \omega, \Omega',</math> and <math>\omega'</math> be the circumcircles of <math>\triangle ABC, \triangle CEF, \triangle BDF,</math> and <math>\triangle ADE,</math> respectively.
 +
 +
In <math>\Omega' \angle MDF = \angle MBF.</math>
 +
 +
In <math>\omega' \angle MDE = \frac {\overset{\Large\frown} {ME}} {2}.</math>
 +
 +
<math>ME</math> is the common chord of <math>\omega</math> and <math>\omega' \implies \angle MOE = \overset{\Large\frown} {ME} \implies</math>
 +
 +
<cmath>\angle MO'o' = \frac {\overset{\Large\frown} {ME}} {2} =  \angle MDE.</cmath>
 +
 +
Similarly, <math>MF</math> is the common chord of <math>\omega</math> and <math>\Omega' \implies  \angle MDF = \angle Moo' = \angle MO'o'.</math>
 +
 +
Similarly, <math>MC</math> is the common chord of <math>\Omega</math> and <math>\omega' \implies  \angle MBC = \angle MOo' \implies</math>
 +
 +
<math>\angle MOo' = \angle MO'o' \implies</math> points <math>M, O, O', o,</math> and <math>o'</math> are concyclic as desired.
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 +
==Triangle of circumcenters==
 +
[[File:Miquel perspector.png|500px|right]]
 +
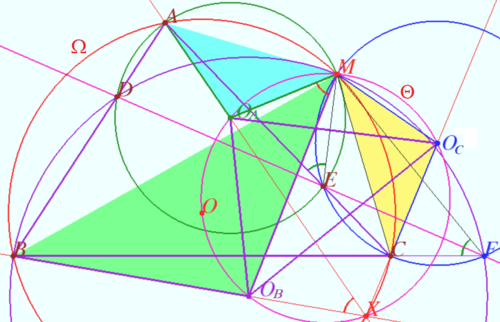
Let four lines made four triangles of a complete quadrilateral.
 +
 +
In the diagram these are <math>\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.</math>
 +
 +
Let points <math>O,O_A, O_B,</math> and <math>O_C</math> be the circumcenters of <math>\triangle ABC, \triangle ADE, \triangle BDF,</math> and <math>\triangle CEF,</math> respectively.
 +
 +
Prove that  <math>\triangle O_AO_BO_C \sim \triangle ABC,</math> and perspector of these triangles point <math>X</math> is the second (different from <math>M</math>) point of intersection <math>\Omega \cap \Theta,</math> where <math>\Omega</math> is circumcircle of <math>\triangle ABC</math> and <math>\Theta</math> is circumcircle of <math>\triangle O_AO_BO_C.</math>
 +
 +
<i><b>Proof</b></i>
 +
 +
Quadrungle <math>MECF</math> is cyclic <math>\implies \angle AEM = \angle BFM \implies</math>
 +
<cmath>\angle AO_AM = 2\angle AEM = 2 \angle BFM = \angle BO_BM.</cmath>
 +
<cmath>\angle CO_CM = 2\angle CFM = 2 \angle BFM = \angle BO_BM.</cmath>
 +
<math>AO_A = MO_A, BO_B = MO_B, CO_C = MO_C \implies \triangle AO_AM \sim \triangle BO_BM \sim \triangle CO_CM.</math>
 +
 +
Spiral similarity sentered at point <math>M</math> with rotation angle <math>\angle AMO_A = \angle BMO_B = CMO_C</math> and the coefficient of homothety <math>\frac {AM}{MO_A} = \frac {BM}{MO_B} =\frac {CM}{MO_C}</math> mapping <math>A</math> to <math>O_A</math>, <math>B</math> to <math>O_B</math>, <math>C</math> to <math>O_C \implies \triangle O_AO_BO_C \sim \triangle ABC.</math>
 +
 +
<math>\triangle AO_AM, \triangle BO_BM, \triangle CO_CM</math> are triangles in double perspective at point <math>M \implies</math>
 +
 +
These triangles are in triple perspective <math>\implies AO_A, BO_B, CO_C</math> are concurrent at the point <math>X.</math>
 +
 +
The rotation angle <math>\triangle AO_AM</math> to <math>\triangle BO_BM</math> is <math>\angle O_AMO_B</math> for sides <math>O_AM</math> and <math>O_BM</math> or angle between <math>AO_A</math> and <math>BO_B</math> which is <math>\angle AXB \implies M O_AO_BX</math> is cyclic <math>\implies M O_AO_BXO_C</math> is cyclic.
 +
 +
Therefore  <math>\angle O_AXO_B = \angle  O_AO_CO_B = \angle ACB \implies ABCX</math> is cyclic as desired.
 +
 +
Similarly, one can prove that <math>\triangle ADE \sim \triangle OO_BO_C, \triangle BDF \sim \triangle OO_AO_C, \triangle CEF \sim \triangle OO_AO_B.</math>
 +
*[[Double perspective triangles]]
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 +
==Analogue of Miquel's point==
 +
[[File:5 circles.png|400px|right]]
 +
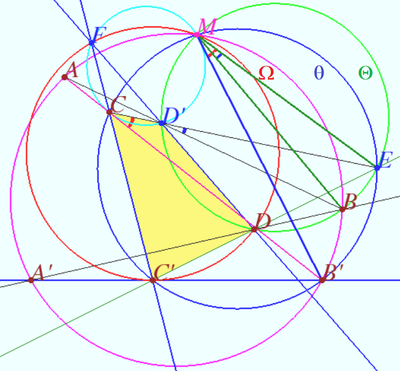
Let inscribed quadrilateral <math>ABB'A'</math> and
 +
 +
points <math>C \in AB', C' \in A'B', D \in A'B</math> be given.
 +
 +
<cmath>\theta = \odot CC'B', \Theta = \odot BDD', M = \theta \cap \Theta,</cmath>
 +
<cmath>E = C'D \cap \odot B'CC', D' = AB \cap CE, F = CC' \cap DD'.</cmath>
 +
Prove that points <math>A, B, B',</math> and <math>M</math> are concyclic.
 +
 +
<i><b>Proof</b></i>
 +
 +
<cmath>\angle BMB' =  \angle EMB' - \angle EMB =
 +
\angle ECB' - \angle ED'B  = \angle BAB' \blacksquare</cmath>
 +
 +
<i><b>Corollary</b></i>
 +
 +
The points <math>F, C, D',</math> and <math>M</math> are concyclic.
 +
 +
The points <math>F, C', D,</math> and <math>M</math> are concyclic.
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
==Six circles crossing point==
 +
[[File:Fixed Miquel point.png|410px|right]]
 +
Let <math>\triangle ABC,</math> point <math>P \in BC,</math> point <math>X \in \Omega = \odot ABC</math> be given.
 +
 +
Denote <math>Y = PX \cap \Omega, D = AX \cap BC, E = AY \cap BC,</math>
 +
<cmath>\omega = \odot ADE, \theta = \odot PEY, \Theta = \odot PDX,</cmath>
 +
<math>\sigma = \odot BP</math> tangent to <math>AB, \Sigma = \odot CP</math> tangent to <math>AC.</math>
 +
 +
Prove that the circles <math>\omega, \Omega, \theta, \Theta, \sigma,</math> and <math>\Sigma</math> have the common point.
 +
 +
<i><b>Proof</b></i>
 +
 +
Let <math>M = \omega \cap \Omega \ne A.</math>
 +
<cmath>\angle YCM = \angle YXM = \angle YAM = \angle EAM = \angle EDM \implies</cmath>
 +
<math>\angle PDM = \angle PXM \implies</math> points <math>M,P,D,</math> and <math>X</math> are concyclic, <math>M \in \Theta.</math> Similarly <math>M \in \theta, M</math> is the Miquel point of quadrungle <math>EDXY.</math>
 +
<cmath>\angle CMY = 180^\circ - \angle CAB - \angle BAY.</cmath>
 +
<cmath>\angle PMY = \angle PEY = \angle ABC - \angle BAY.</cmath>
 +
<cmath>\angle PMC = \angle CMY - \angle PMY = (180^\circ - \angle CAB - \angle BAY) - (\angle ABC - \angle BAY) = \angle ACB.</cmath>
 +
<math>\angle PMC = \angle ACB \implies AC</math> is tangent to <math>\Sigma.</math> Similarly, <math>AB</math> is tangent to <math>\sigma.</math>
  
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''

Latest revision as of 15:18, 21 October 2024

Miquel and Steiner's quadrilateral theorem

4 Miquel circles.png

Let four lines made four triangles of a complete quadrilateral. In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$

Prove that the circumcircles of all four triangles meet at a single point.

Proof

Let circumcircle of $\triangle ABC$ circle $\Omega$ cross the circumcircle of $\triangle CEF$ circle $\omega$ at point $M.$

Let $AM$ cross $\omega$ second time in the point $G.$

$CMGF$ is cyclic $\implies \angle BCM = \angle MGF.$

$AMCB$ is cyclic $\implies \angle BCM + \angle BAM = 180^\circ \implies$

$\angle BAG + \angle AGF = 180^\circ \implies AB||GF.$

$CMGF$ is cyclic $\implies \angle AME = \angle EFG.$

$AD||GF \implies \angle ADE + \angle DFG = 180^\circ \implies \angle ADE + \angle AME = 180^\circ \implies$

$ADEM$ is cyclic and circumcircle of $\triangle ADE$ contain the point $M.$

Similarly circumcircle of $\triangle BDF$ contain the point $M$ as desired.

vladimir.shelomovskii@gmail.com, vvsss

Circle of circumcenters

Miquel point.png

Let four lines made four triangles of a complete quadrilateral. In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$

Prove that the circumcenters of all four triangles and point $M$ are concyclic.

Proof

Let $\Omega, \omega, \Omega',$ and $\omega'$ be the circumcircles of $\triangle ABC, \triangle CEF, \triangle BDF,$ and $\triangle ADE,$ respectively.

In $\Omega' \angle MDF = \angle MBF.$

In $\omega' \angle MDE = \frac {\overset{\Large\frown} {ME}} {2}.$

$ME$ is the common chord of $\omega$ and $\omega' \implies \angle MOE = \overset{\Large\frown} {ME} \implies$

\[\angle MO'o' = \frac {\overset{\Large\frown} {ME}} {2} = \angle MDE.\]

Similarly, $MF$ is the common chord of $\omega$ and $\Omega' \implies \angle MDF = \angle Moo' = \angle MO'o'.$

Similarly, $MC$ is the common chord of $\Omega$ and $\omega' \implies \angle MBC = \angle MOo' \implies$

$\angle MOo' = \angle MO'o' \implies$ points $M, O, O', o,$ and $o'$ are concyclic as desired.

vladimir.shelomovskii@gmail.com, vvsss

Triangle of circumcenters

Miquel perspector.png

Let four lines made four triangles of a complete quadrilateral.

In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$

Let points $O,O_A, O_B,$ and $O_C$ be the circumcenters of $\triangle ABC, \triangle ADE, \triangle BDF,$ and $\triangle CEF,$ respectively.

Prove that $\triangle O_AO_BO_C \sim \triangle ABC,$ and perspector of these triangles point $X$ is the second (different from $M$) point of intersection $\Omega \cap \Theta,$ where $\Omega$ is circumcircle of $\triangle ABC$ and $\Theta$ is circumcircle of $\triangle O_AO_BO_C.$

Proof

Quadrungle $MECF$ is cyclic $\implies \angle AEM = \angle BFM \implies$ \[\angle AO_AM = 2\angle AEM = 2 \angle BFM = \angle BO_BM.\] \[\angle CO_CM = 2\angle CFM = 2 \angle BFM = \angle BO_BM.\] $AO_A = MO_A, BO_B = MO_B, CO_C = MO_C \implies \triangle AO_AM \sim \triangle BO_BM \sim \triangle CO_CM.$

Spiral similarity sentered at point $M$ with rotation angle $\angle AMO_A = \angle BMO_B = CMO_C$ and the coefficient of homothety $\frac {AM}{MO_A} = \frac {BM}{MO_B} =\frac {CM}{MO_C}$ mapping $A$ to $O_A$, $B$ to $O_B$, $C$ to $O_C \implies \triangle O_AO_BO_C \sim \triangle ABC.$

$\triangle AO_AM, \triangle BO_BM, \triangle CO_CM$ are triangles in double perspective at point $M \implies$

These triangles are in triple perspective $\implies AO_A, BO_B, CO_C$ are concurrent at the point $X.$

The rotation angle $\triangle AO_AM$ to $\triangle BO_BM$ is $\angle O_AMO_B$ for sides $O_AM$ and $O_BM$ or angle between $AO_A$ and $BO_B$ which is $\angle AXB \implies M O_AO_BX$ is cyclic $\implies M O_AO_BXO_C$ is cyclic.

Therefore $\angle O_AXO_B = \angle O_AO_CO_B = \angle ACB \implies ABCX$ is cyclic as desired.

Similarly, one can prove that $\triangle ADE \sim \triangle OO_BO_C, \triangle BDF \sim \triangle OO_AO_C, \triangle CEF \sim \triangle OO_AO_B.$

vladimir.shelomovskii@gmail.com, vvsss

Analogue of Miquel's point

5 circles.png

Let inscribed quadrilateral $ABB'A'$ and

points $C \in AB', C' \in A'B', D \in A'B$ be given.

\[\theta = \odot CC'B', \Theta = \odot BDD', M = \theta \cap \Theta,\] \[E = C'D \cap \odot B'CC', D' = AB \cap CE, F = CC' \cap DD'.\] Prove that points $A, B, B',$ and $M$ are concyclic.

Proof

\[\angle BMB' = \angle EMB' - \angle EMB = \angle ECB' - \angle ED'B = \angle BAB' \blacksquare\]

Corollary

The points $F, C, D',$ and $M$ are concyclic.

The points $F, C', D,$ and $M$ are concyclic.

vladimir.shelomovskii@gmail.com, vvsss

Six circles crossing point

Fixed Miquel point.png

Let $\triangle ABC,$ point $P \in BC,$ point $X \in \Omega = \odot ABC$ be given.

Denote $Y = PX \cap \Omega, D = AX \cap BC, E = AY \cap BC,$ \[\omega = \odot ADE, \theta = \odot PEY, \Theta = \odot PDX,\] $\sigma = \odot BP$ tangent to $AB, \Sigma = \odot CP$ tangent to $AC.$

Prove that the circles $\omega, \Omega, \theta, \Theta, \sigma,$ and $\Sigma$ have the common point.

Proof

Let $M = \omega \cap \Omega \ne A.$ \[\angle YCM = \angle YXM = \angle YAM = \angle EAM = \angle EDM \implies\] $\angle PDM = \angle PXM \implies$ points $M,P,D,$ and $X$ are concyclic, $M \in \Theta.$ Similarly $M \in \theta, M$ is the Miquel point of quadrungle $EDXY.$ \[\angle CMY = 180^\circ - \angle CAB - \angle BAY.\] \[\angle PMY = \angle PEY = \angle ABC - \angle BAY.\] \[\angle PMC = \angle CMY - \angle PMY = (180^\circ - \angle CAB - \angle BAY) - (\angle ABC - \angle BAY) = \angle ACB.\] $\angle PMC = \angle ACB \implies AC$ is tangent to $\Sigma.$ Similarly, $AB$ is tangent to $\sigma.$

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Miquel%27s_point&oldid=230277"