Difference between revisions of "2003 AMC 12B Problems/Problem 21"
Isabelchen (talk | contribs) m (→Solution 2 (Analytic Geometry)) |
Math Kirby (talk | contribs) m |
||
| (3 intermediate revisions by one other user not shown) | |||
| Line 15: | Line 15: | ||
\end{align*}</cmath> | \end{align*}</cmath> | ||
| − | It follows that <math>0 < \alpha < \frac {\pi}3</math>, and the probability is <math>\frac{\pi/3}{\pi} = \ | + | It follows that <math>0 < \alpha < \frac {\pi}3</math>, and the probability is <math>\frac{\pi/3}{\pi} = \boxed{\textbf{(D) } \frac13 }</math>. |
==Solution 2 (Analytic Geometry)== | ==Solution 2 (Analytic Geometry)== | ||
| Line 38: | Line 38: | ||
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen] | ~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen] | ||
| + | |||
| + | ==Solution 3 (Geometric Probability)== | ||
| + | |||
| + | Setting <math>A = (0,0)</math> we get that <math>B = (8,0)</math>, after assuming segment AB to be straight in the x-direction relative to our coordinate system (in other words, due to symmetrically we can set <math>x = 8</math> for point B). This gives <math>C = (8 + 5cos(\alpha), 5sin(\alpha))</math>. Using the distance formula we get <math>sqrt((8 + 5cos(\alpha))^2 + (5sin(\alpha))^2) < 7</math>. After algebra, this simplifies to <math>cos(\alpha) < -\frac{1}{2}</math>. After evaluating the constraints of the problem, we land on option (D). | ||
| + | |||
| + | ~PeterDoesPhysics | ||
== See also == | == See also == | ||
Latest revision as of 09:23, 20 September 2024
Contents
Problem
An object moves ![]() cm in a straight line from
cm in a straight line from ![]() to
to ![]() , turns at an angle
, turns at an angle ![]() , measured in radians and chosen at random from the interval
, measured in radians and chosen at random from the interval ![]() , and moves
, and moves ![]() cm in a straight line to
cm in a straight line to ![]() . What is the probability that
. What is the probability that ![]() ?
?
![]()
Solution 1 (Trigonometry)
By the Law of Cosines,

It follows that ![]() , and the probability is
, and the probability is ![]() .
.
Solution 2 (Analytic Geometry)
![]() , let the object turn clockwise.
, let the object turn clockwise.
Let ![]() ,
, ![]() .
.
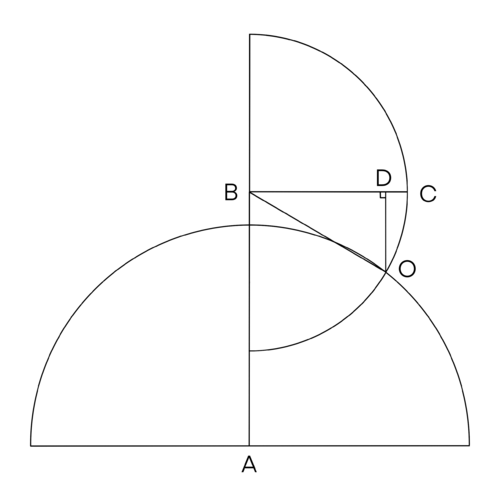
Note that the possible points of ![]() create a semi-circle of radius
create a semi-circle of radius ![]() and center
and center ![]() . The area where
. The area where ![]() is enclosed by a circle of radius
is enclosed by a circle of radius ![]() and center
and center ![]() . The probability that
. The probability that ![]() is
is ![]() .
.
The function of ![]() is
is ![]() , the function of
, the function of ![]() is
is ![]() .
.
![]() is the point that satisfies the system of equations:
is the point that satisfies the system of equations: 
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Note that ![]() is a
is a ![]() triangle, as
triangle, as ![]() ,
, ![]() ,
, ![]() . As a result
. As a result ![]() ,
, ![]() .
.
Therefore the probability that ![]() is
is ![]()
Solution 3 (Geometric Probability)
Setting ![]() we get that
we get that ![]() , after assuming segment AB to be straight in the x-direction relative to our coordinate system (in other words, due to symmetrically we can set
, after assuming segment AB to be straight in the x-direction relative to our coordinate system (in other words, due to symmetrically we can set ![]() for point B). This gives
for point B). This gives ![]() . Using the distance formula we get
. Using the distance formula we get ![]() . After algebra, this simplifies to
. After algebra, this simplifies to ![]() . After evaluating the constraints of the problem, we land on option (D).
. After evaluating the constraints of the problem, we land on option (D).
~PeterDoesPhysics
See also
| 2003 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 20 |
Followed by Problem 22 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.