Difference between revisions of "2002 AIME I Problems/Problem 2"
m |
Cheetahboy93 (talk | contribs) m (→Solution 2) |
||
| (6 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
| − | The diagram shows twenty congruent | + | The diagram shows twenty congruent [[circle]]s arranged in three rows and enclosed in a rectangle. The circles are tangent to one another and to the sides of the rectangle as shown in the diagram. The [[ratio]] of the longer dimension of the rectangle to the shorter dimension can be written as <math>\dfrac{1}{2}(\sqrt{p}-q)</math> where <math>p</math> and <math>q</math> are positive integers. Find <math>p+q</math>. |
<center>[[Image:AIME_2002I_Problem_02.png]]</center> | <center>[[Image:AIME_2002I_Problem_02.png]]</center> | ||
== Solution == | == Solution == | ||
| − | {{ | + | Let the [[radius]] of the circles be <math>r</math>. The longer dimension of the rectangle can be written as <math>14r</math>, and by the [[Pythagorean Theorem]], we find that the shorter dimension is <math>2r\left(\sqrt{3}+1\right)</math>. |
| + | |||
| + | Therefore, <math>\frac{14r}{2r\left(\sqrt{3}+1\right)}= \frac{7}{\sqrt{3} + 1} \cdot \left[\frac{\sqrt{3}-1}{\sqrt{3}-1}\right] = \frac{1}{2}\left(7\sqrt{3} - 7\right) = \frac{1}{2}\left(\sqrt{p}-q\right)</math>. Thus we have <math>p=147</math> and <math>q=7</math>, so <math>p+q=\boxed{154}</math>. | ||
| + | |||
| + | == Solution 2 == | ||
| + | Since we only care about the ''ratio'' between the longer side and shorter side, we can set the longer side to <math>14</math>. So, this means that each of the radii is <math>1</math>. Now, we connect the radii of three circles such that they form an equilateral triangle with side length 4. Obviously, the height this triangle is <math>2\sqrt{3}</math>, and the shorter side of the triangle is therefore <math>2\sqrt{3}+2</math> and we use simplification similar to as showed above, and we reach the result <math>\frac{1}{2} \cdot (\sqrt{147}-7)</math> and the final answer is <math>147+7 = \boxed{154}</math>. | ||
== See also == | == See also == | ||
| − | + | {{AIME box|year=2002|n=I|num-b=1|num-a=3}} | |
| − | |||
| − | |||
| − | + | [[Category:Intermediate Geometry Problems]] | |
| + | {{MAA Notice}} | ||
Latest revision as of 19:21, 16 September 2024
Contents
Problem
The diagram shows twenty congruent circles arranged in three rows and enclosed in a rectangle. The circles are tangent to one another and to the sides of the rectangle as shown in the diagram. The ratio of the longer dimension of the rectangle to the shorter dimension can be written as 
where 
and 
are positive integers. Find 
.
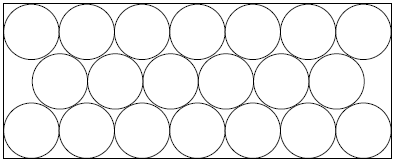
Solution
Let the radius of the circles be 
. The longer dimension of the rectangle can be written as 
, and by the Pythagorean Theorem, we find that the shorter dimension is 
.
Therefore, ![$\frac{14r}{2r\left(\sqrt{3}+1\right)}= \frac{7}{\sqrt{3} + 1} \cdot \left[\frac{\sqrt{3}-1}{\sqrt{3}-1}\right] = \frac{1}{2}\left(7\sqrt{3} - 7\right) = \frac{1}{2}\left(\sqrt{p}-q\right)$](http://latex.artofproblemsolving.com/b/a/c/bac1c28eb0b7334f0866a1e9a58d97956ee24c78.png)
. Thus we have 
and 
, so 
.
Solution 2
Since we only care about the ratio between the longer side and shorter side, we can set the longer side to 
. So, this means that each of the radii is 
. Now, we connect the radii of three circles such that they form an equilateral triangle with side length 4. Obviously, the height this triangle is 
, and the shorter side of the triangle is therefore 
and we use simplification similar to as showed above, and we reach the result 
and the final answer is 
.
See also
| 2002 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 1 |
Followed by Problem 3 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
