Difference between revisions of "Disphenoid"

Revision as of 19:07, 14 August 2024

Disphenoid is a tetrahedron whose four faces are congruent acute-angled triangles.

Main

a) A tetrahedron $ABCD$ is a disphenoid iff $AB = CD, AC = BD, AD = BC.$

b) A tetrahedron is a disphenoid iff its circumscribed parallelepiped is right-angled.

c) Let $AB = a, AC = b, AD = c.$ The squares of the lengths of sides its circumscribed parallelepiped and the bimedians are: $AB'^2 = l^2 = \frac {a^2-b^2+ c^2}{2}, AC'^2 = m^2 = \frac {a^{2}-b^{2}+c^{2}}{2},$ $AD'^2 = n^2 = \frac {-a^{2}+b^{2}+c^{2}}{2}$ The circumscribed sphere has radius (the circumradius): $R=\sqrt {\frac {a^2+b^2+c^2}{8}}.$

The volume of a disphenoid is: $V= \frac {lmn}{3} = \sqrt {\frac {(a^2+b^2-c^2)(a^2-b^2+c^2)(-a^{2}+b^{2}+c^{2})}{72}}$ Each height of disphenoid $ABCD$ is $h=\frac {3V}{[ABC]},$ the inscribed sphere has radius: $r=\frac {3V}{4[ABC]},$ where $[ABC]$ is the area of $\triangle ABC.$

Proof

a) $AB \ne BC, AB \ne AD, \triangle ABC = \triangle BAD = \triangle CDA = \triangle DCB.$

$AB \ne AD, AB \ne BD$ because in $\triangle ABD$ there is no equal sides.

Let consider $\triangle BCD.$

$BD \ne AB, BC \ne AB,$ but one of sides need be equal $AB,$ so $AB = CD \implies AC = BD, AD = BC.$

b) Any tetrahedron can be assigned a parallelepiped by drawing a plane through each edge of the tetrahedron parallel to the opposite edge.

$AB = CD = C'D' \implies AD'BC'$ is parallelogram with equal diagonals, i.e. rectangle.

Similarly, $AB'CD'$ and $AB'DC'$ are rectangles.

If $AD'BC'$ is rectangle, then $AB = C'D' = CD.$

Similarly, $AC = BD, AD = BC \implies ABCD$ is a disphenoid.

c) $AB^2 = a^2 = AC'^2 + BC'^2 = m^2 + AD'^2 = m^2 + n^2.$

Similarly, $AC^2 = b^2 = l^2 + n^2, AD^2 = c^2 = l^2 + m^2 \implies 2(l^2 + m^2 + n^2) = a^2 + b^2 + c^2 \implies$ $l^2 = l^2 + m^2 + n^2 - (m^2 + n^2) = \frac {a^2 + b^2 + c^2}{2} - a^2 = \frac {-a^2 + b^2 + c^2}{2}.$

Similarly, $m^2 = \frac {a^2 - b^2 + c^2}{2}, n^2 = \frac {a^2 + b^2 - c^2}{2}.$

Let $E$ be the midpoint $AC$ , $E'$ be the midpoint $BD \implies$

$EE' = AC' = m = \sqrt {\frac {a^2 - b^2 + c^2}{2}}$ is the bimedian of $AC$ and $BD.$ $EE' || AC' \implies EE' \perp AC, EE' \perp BD.$

The circumscribed sphere of $ABCD$ is the circumscribed sphere of $AB'CD'C'DA'C,$ so it is $\frac {AA'}{2} = \sqrt {\frac {a^2+b^2+c^2}{8}}.$

The volume of a disphenoid is third part of the volume of $AB'CD'C'DA'C,$ so: $V= \frac {l \cdot m \cdot n}{3} = \sqrt {\frac {(a^2+b^2-c^2)(a^2-b^2+c^2)(-a^{2}+b^{2}+c^{2})}{72}}.$ The volume of a disphenoid is $V = \frac {1}{3} h [ABC] \implies h = \frac{3V}{[ABC]},$ where $h$ is any height.

The inscribed sphere has radius $r = \frac{h}{4}.$ $72 V^2 = (a^2+b^2-c^2) \cdot (a^2-b^2+c^2) \cdot (-a^2+b^2+c^2) =-a^6+a^4 b^2+a^4 c^2+a^2 b^4+a^2 c^4-b^6+b^4 c^2+b^2 c^4-c^6 -2a^2 b^2 c^2,$ $16 [ABC]^2 = (a+b+c)(a+b-c)(a-b+c)(-a+b+c) = -a^4+2a^2b^2+2a^2c^2-b^4+2b^2c^2-c^4,$ $8 R^2 = a^2+b^2+c^2,$ $128 R^2 [ABC]^2 = -a^6+a^4 b^2+a^4 c^2+a^2 b^4 +a^2 c^4-b^6+b^4 c^2+b^2 c^4-c^6 + 6a^2 b^2 c^2.$

Therefore $16 R^2 [ABC]^2 = a^2 b^2 c^2 + 9 V^2.$

vladimir.shelomovskii@gmail.com, vvsss

Constructing

Let triangle $ABC$ be given. Сonstruct the disphenoid $ABCD.$

Solution

Let $\triangle A_1B_1C_1$ be the anticomplementary triangle of $\triangle ABC, M$ be the midpoint $BC.$

Then $M$ is the midpoint of segment $AA_1 \implies$

$2MA' = AD, MA' || AD \implies A'$ is the midpoint $A_1D.$

Similarly, $B'$ is the midpoint $B_1D, C'$ is the midpoint $C_1D.$

So, $\angle A_1DB_1 = \angle B_1DC_1 = \angle C_1DA_1 = 90^\circ.$

Let $A_1A_0, B_1B_0, C_1C_0$ be the altitudes of $\triangle A_1B_1C_1, H$ be the orthocenter of $\triangle A_1B_1C_1 \implies DH \perp ABC.$

To construct the disphenoid $ABCD$ using given triangle $ABC$ we need:

1) Construct $\triangle A_1B_1C_1,$ the anticomplementary triangle of $\triangle ABC,$

2) Find the orthocenter $H$ of $\triangle A_1B_1C_1.$

3) Construct the perpendicular from point $H$ to plane $ABC.$

4) Find the point $D$ in this perpendicular such that $AD = BC.$

vladimir.shelomovskii@gmail.com, vvsss

@@ Line 63: / Line 63: @@
 Therefore <math>16 R^2 [ABC]^2 = a^2 b^2 c^2 + 9 V^2.</math>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Constructing==
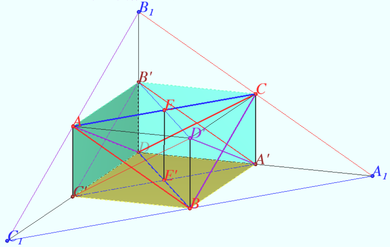
+[[File:Disphenoid -parallelepiped A.png|390px|right]]
+Let triangle <math>ABC</math> be given. Сonstruct the disphenoid <math>ABCD.</math>
+<i><b>Solution</b></i>
+Let <math>\triangle A_1B_1C_1</math> be the anticomplementary triangle of <math>\triangle ABC, M</math> be the midpoint <math>BC.</math>
+Then <math>M</math> is the midpoint of segment <math>AA_1 \implies</math>
+<math>2MA' = AD, MA' || AD \implies A'</math> is the midpoint <math>A_1D.</math>
+Similarly, <math>B'</math> is the midpoint <math>B_1D, C'</math> is the midpoint <math>C_1D.</math>
+So, <math>\angle A_1DB_1 = \angle B_1DC_1 = \angle C_1DA_1 = 90^\circ.</math>
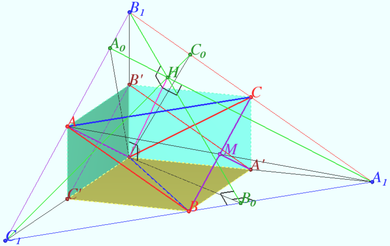
+Let <math>A_1A_0, B_1B_0, C_1C_0</math> be the altitudes of <math>\triangle A_1B_1C_1, H</math> be the orthocenter of <math>\triangle A_1B_1C_1 \implies DH \perp ABC.</math>
+To construct the disphenoid <math>ABCD</math> using given triangle <math>ABC</math> we need:
+) Construct <math>\triangle A_1B_1C_1,</math> the anticomplementary triangle of <math>\triangle ABC,</math>
+) Find the orthocenter <math>H</math> of <math>\triangle A_1B_1C_1.</math>
+) Construct the perpendicular from point <math>H</math> to plane <math>ABC.</math>
+) Find the point <math>D</math> in this perpendicular such that <math>AD = BC.</math>
 '''vladimir.shelomovskii@gmail.com, vvsss'''

Page

Toolbox

Search

Difference between revisions of "Disphenoid"

Revision as of 19:07, 14 August 2024

Main

Constructing