Difference between revisions of "2003 AMC 10A Problems/Problem 22"

Revision as of 10:17, 15 January 2008

Problem

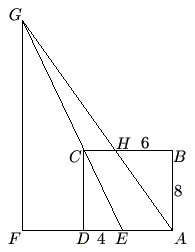
In rectangle $ABCD$ , we have $AB=8$ , $BC=9$ , $H$ is on $BC$ with $BH=6$ , $E$ is on $AD$ with $DE=4$ , line $EC$ intersects line $AH$ at $G$ , and $F$ is on line $AD$ with $GF \perp AF$ . Find the length of $GF$ .

$\mathrm{(A) \ } 16\qquad \mathrm{(B) \ } 20\qquad \mathrm{(C) \ } 24\qquad \mathrm{(D) \ } 28\qquad \mathrm{(E) \ } 30$

Solution

Since $ABCD$ is a rectangle, $CD=AB=8$ .

Since $ABCD$ is a rectangle and $GF \perp AF$ , $\angle GFE = \angle CDE = \angle ABC = 90^\circ$ .

Since $ABCD$ is a rectangle, $AD || BC$ .

So, $AH$ is a transversal, and $\angle GAF = \angle AHB$ .

This is sufficient to prove that $GFE \approx CDE$ and $GFA \approx ABH$ .

Using ratios:

$\frac{GF}{FE}=\frac{CD}{DE}$

$\frac{GF}{FD+4}=\frac{8}{4}=2$

$GF=2 \cdot (FD+4)=2 \cdot FD+8$

$\frac{GF}{FA}=\frac{AB}{BH}$

$\frac{GF}{FD+9}=\frac{8}{6}=\frac{4}{3}$

$GF=\frac{4}{3} \cdot (FD+9)=\frac{4}{3} \cdot FD+12$

Since $GF$ can't have 2 different lengths, both expressions for $GF$ must be equal.

$2 \cdot FD+8=\frac{4}{3} \cdot FD+12$

$\frac{2}{3} \cdot FD=4$

$FD=6$

$GF=2 \cdot FD+8=2\cdot6+8=20 \Rightarrow B$

2003 AMC 10A (Problems • Answer Key • Resources)
Preceded by Problem 21	Followed by Problem 23
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

@@ Line 42: / Line 42: @@
 == See Also ==
-*[[2003 AMC 10A Problems]]
+{{AMC10 box|year=2003|ab=A|num-b=21|num-a=23}}
-*[[2003 AMC 10A Problems/Problem 21|Previous Problem]]
-*[[2003 AMC 10A Problems/Problem 23|Next Problem]]
 [[Category:Introductory Geometry Problems]]

Page

Toolbox

Search

Difference between revisions of "2003 AMC 10A Problems/Problem 22"

Revision as of 10:17, 15 January 2008

Problem

Solution

See Also