Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Tucker circles"

(Created page with "The Tucker circles are a generalization of the cosine circle and first Lemoine circle.")
 
Line 1: Line 1:
 
The Tucker circles are a generalization of the cosine circle and first Lemoine circle.
 
The Tucker circles are a generalization of the cosine circle and first Lemoine circle.
 +
==Tucker circle==
 +
[[File:Tucker circle.png|450px|right]]
 +
[[File:Tucker circle A.png|450px|right]]
 +
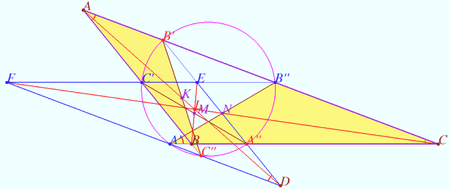
Let triangle <math>ABC</math> be given. <math>O</math> is it’s circumcenter, <math>L</math> is it’s Lemoine point.
 +
 +
Let homothety centered at <math>L</math> with factor <math>k</math> maps <math>\triangle ABC</math> into <math>\triangle DEF</math>.
 +
 +
Denote the crosspoints of sidelines these triangles as
 +
<cmath>A' = BC \cap DF, B' = AC \cap DE, C' = AB \cap EF,</cmath>
 +
<cmath> A'' = BC \cap DE, B'' = AC \cap EF, C'' = AB \cap DF.</cmath>
 +
 +
Prove that points <math>A', B', C', A'', B'',</math> and <math>C''</math> lies on the circle centered at <math>LO</math> (Tucker circle).
 +
 +
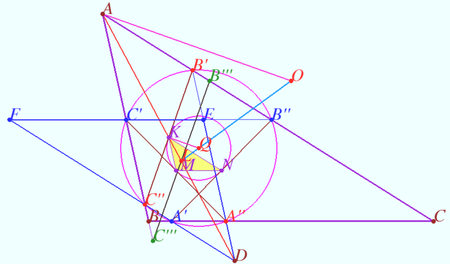
<i><b>Proof</b></i>
 +
 +
<math>AB' || C''D, AC'' || B'D \implies AB'DC''</math> is the parallelogram.
 +
 +
Denote <math>K = AD \cap B'C'', AK = KD, B'K = KC'' \implies</math>
 +
<math>B'C''</math> is antiparallel to <math>BC.</math>
 +
 +
Similarly, <math>A''C'</math> is antiparallel to <math>AC, A'B''</math> is antiparallel to <math>AB.</math>
 +
 +
<math>M = BE \cap A''C'</math> is midpoint <math>BE, N =  A'B'' \cap CF</math> is the midpoint <math>CF.</math>
 +
 +
<math>\triangle AB'C'' \sim \triangle ABC.</math>
 +
 +
<math>\frac {LD}{AL} = k, AL = LD \implies  \frac {AK}{AL} = \frac{2}{k+1}, \frac {KL}{AL} = \frac{1-k}{1+k}.</math>
 +
 +
Similarly, <math>\frac {BM}{BL} = \frac {CN}{CL} = \frac {AK}{AL} =\frac{2}{k+1}, \frac {KL}{AL} = \frac{ML}{BM}=  \frac {NL}{CL} = \frac{1-k}{1+k}.</math>
 +
 +
Let <math>B'''C'''</math> be the symmedian <math>BC</math> through <math>L.</math>
 +
<cmath>B'''C''' || B'C'' \implies B'C'' = B'''C''' \cdot  \frac {AK}{AL} =\frac{2B'''C'''}{k+1}.</cmath>
 +
 +
It is known that three symmedians through <math>L</math> are equal, so <math>A''C' = C''B' = B''A' = \frac{2B'''C'''}{k+1}.</math>
 +
 +
<math>\triangle KMN</math> is homothetic to <math>\triangle ABC</math> with center <math>L</math> and factor <math>\frac{1-k}{1+k}.</math>
 +
 +
So segments <math>A''C' = C''B' = B''A'</math> are tangents to <math>\odot KMN</math> and points of contact are the midpoints of these segments.
 +
 +
Denote <math>Q</math> the circumcenter of <math>\triangle KMN, Q \in LO.</math>
 +
 +
Therefore <math>A'Q = B'Q = C'Q = A''Q = B''Q = C''Q. \blacksquare</math>
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''

Revision as of 05:32, 4 August 2024

The Tucker circles are a generalization of the cosine circle and first Lemoine circle.

Tucker circle

Tucker circle.png
Tucker circle A.png

Let triangle $ABC$ be given. $O$ is it’s circumcenter, $L$ is it’s Lemoine point.

Let homothety centered at $L$ with factor $k$ maps $\triangle ABC$ into $\triangle DEF$.

Denote the crosspoints of sidelines these triangles as \[A' = BC \cap DF, B' = AC \cap DE, C' = AB \cap EF,\] \[A'' = BC \cap DE, B'' = AC \cap EF, C'' = AB \cap DF.\]

Prove that points $A', B', C', A'', B'',$ and $C''$ lies on the circle centered at $LO$ (Tucker circle).

Proof

$AB' || C''D, AC'' || B'D \implies AB'DC''$ is the parallelogram.

Denote $K = AD \cap B'C'', AK = KD, B'K = KC'' \implies$ $B'C''$ is antiparallel to $BC.$

Similarly, $A''C'$ is antiparallel to $AC, A'B''$ is antiparallel to $AB.$

$M = BE \cap A''C'$ is midpoint $BE, N = A'B'' \cap CF$ is the midpoint $CF.$

$\triangle AB'C'' \sim \triangle ABC.$

$\frac {LD}{AL} = k, AL = LD \implies \frac {AK}{AL} = \frac{2}{k+1}, \frac {KL}{AL} = \frac{1-k}{1+k}.$

Similarly, $\frac {BM}{BL} = \frac {CN}{CL} = \frac {AK}{AL} =\frac{2}{k+1}, \frac {KL}{AL} = \frac{ML}{BM}= \frac {NL}{CL} = \frac{1-k}{1+k}.$

Let $B'''C'''$ be the symmedian $BC$ through $L.$ \[B'''C''' || B'C'' \implies B'C'' = B'''C''' \cdot \frac {AK}{AL} =\frac{2B'''C'''}{k+1}.\]

It is known that three symmedians through $L$ are equal, so $A''C' = C''B' = B''A' = \frac{2B'''C'''}{k+1}.$

$\triangle KMN$ is homothetic to $\triangle ABC$ with center $L$ and factor $\frac{1-k}{1+k}.$

So segments $A''C' = C''B' = B''A'$ are tangents to $\odot KMN$ and points of contact are the midpoints of these segments.

Denote $Q$ the circumcenter of $\triangle KMN, Q \in LO.$

Therefore $A'Q = B'Q = C'Q = A''Q = B''Q = C''Q. \blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Tucker_circles&oldid=224405"