Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2017 AMC 12B Problems/Problem 24"
m (→‎Solution 6)
 
(10 intermediate revisions by 3 users not shown)
Line 8: Line 8:
  
 
Let <math>CD=1</math>, <math>BC=x</math>, and <math>AB=x^2</math>. Note that <math>AB/BC=x</math>. By the Pythagorean Theorem, <math>BD=\sqrt{x^2+1}</math>. Since <math>\triangle BCD \sim \triangle ABC \sim \triangle CEB</math>, the ratios of side lengths must be equal. Since <math>BC=x</math>, <math>CE=\frac{x^2}{\sqrt{x^2+1}}</math> and <math>BE=\frac{x}{\sqrt{x^2+1}}</math>. Let F be a point on <math>\overline{BC}</math> such that <math>\overline{EF}</math> is an altitude of triangle <math>CEB</math>. Note that <math>\triangle CEB \sim \triangle CFE \sim \triangle EFB</math>. Therefore, <math>BF=\frac{x}{x^2+1}</math> and <math>CF=\frac{x^3}{x^2+1}</math>. Since <math>\overline{CF}</math> and <math>\overline{BF}</math> form altitudes of triangles <math>CED</math> and <math>BEA</math>, respectively, the areas of these triangles can be calculated. Additionally, the area of triangle <math>BEC</math> can be calculated, as it is a right triangle. Solving for each of these yields:
 
Let <math>CD=1</math>, <math>BC=x</math>, and <math>AB=x^2</math>. Note that <math>AB/BC=x</math>. By the Pythagorean Theorem, <math>BD=\sqrt{x^2+1}</math>. Since <math>\triangle BCD \sim \triangle ABC \sim \triangle CEB</math>, the ratios of side lengths must be equal. Since <math>BC=x</math>, <math>CE=\frac{x^2}{\sqrt{x^2+1}}</math> and <math>BE=\frac{x}{\sqrt{x^2+1}}</math>. Let F be a point on <math>\overline{BC}</math> such that <math>\overline{EF}</math> is an altitude of triangle <math>CEB</math>. Note that <math>\triangle CEB \sim \triangle CFE \sim \triangle EFB</math>. Therefore, <math>BF=\frac{x}{x^2+1}</math> and <math>CF=\frac{x^3}{x^2+1}</math>. Since <math>\overline{CF}</math> and <math>\overline{BF}</math> form altitudes of triangles <math>CED</math> and <math>BEA</math>, respectively, the areas of these triangles can be calculated. Additionally, the area of triangle <math>BEC</math> can be calculated, as it is a right triangle. Solving for each of these yields:
−
<cmath>[BEC]=[CED]=[BEA]=(x^3)/(2(x^2+1))</cmath>
+
 
−
<cmath>[ABCD]=[AED]+[DEC]+[CEB]+[BEA]</cmath>
+
\begin{align*}
−
<cmath>(AB+CD)(BC)/2= 17*[CEB]+ [CEB] + [CEB] + [CEB]</cmath>
+
[BEC] &=[CED]=[BEA]=\frac{x^3}{2(x^2+1)} \\
−
<cmath>(x^3+x)/2=(20x^3)/(2(x^2+1))</cmath>
+
[ABCD] &=[AED]+[DEC]+[CEB]+[BEA] \\
−
<cmath>(x)(x^2+1)=20x^3/(x^2+1)</cmath>
+
\frac{(BC)(AB+CD)}{2} &= 17*[CEB]+ [CEB] + [CEB] + [CEB] \\
−
<cmath>(x^2+1)^2=20x^2</cmath>
+
\frac{x^3+x}{2} &= \frac{20x^3}{2(x^2+1)} \\
−
<cmath>x^4-18x^2+1=0 \implies x^2=9+4\sqrt{5}=4+2(2\sqrt{5})+5</cmath>
+
\frac{x}{x^2+1} &= \frac{20x^3}{x^2+1} \\
 +
(x^2+1)^2 &=20x^2 \\
 +
x^4-18x^2+1 &=0 \implies x^2=9+4\sqrt{5}=4+2(2\sqrt{5})+5 \\
 +
\end{align*}
 +
 
 
Therefore, the answer is <math>\boxed{\textbf{(D) } 2+\sqrt{5}}</math>
 
Therefore, the answer is <math>\boxed{\textbf{(D) } 2+\sqrt{5}}</math>
−
 
  
 
==Solution 2==  
 
==Solution 2==  
Line 30: Line 33:
 
==Solution 3==
 
==Solution 3==
  
−
Diagram by [https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
+
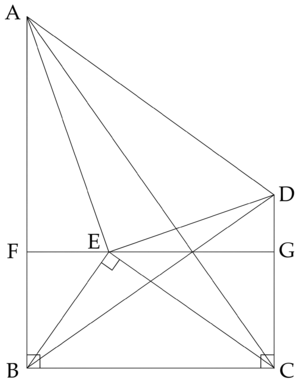
[[File:2017AMC12BP24.png|300px|center]]
  
 
Let <math>AB = a</math>, <math>BC = b</math>, <math>AC = \sqrt{a^2+b^2}</math>
 
Let <math>AB = a</math>, <math>BC = b</math>, <math>AC = \sqrt{a^2+b^2}</math>
Line 36: Line 39:
 
Note that <math>E</math> cannot be the intersection of <math>AC</math> and <math>BD</math>, as that would mean <math>[AED] = [CEB]</math>
 
Note that <math>E</math> cannot be the intersection of <math>AC</math> and <math>BD</math>, as that would mean <math>[AED] = [CEB]</math>
  
 +
<cmath>\because \triangle BCD \sim \triangle ABC, \quad \therefore \frac{CD}{BC} = \frac{BC}{AB}, \quad CD = BC \cdot \frac{BC}{AB} = b \cdot \frac{b}{a} = \frac{b^2}{a}</cmath>
 +
 +
<cmath>[CEB] = ( \frac{BC}{AC} )^2 \cdot [ABC] = ( \frac{b}{ \sqrt{a^2+b^2} } )^2 \cdot \frac{ab}{2} = \frac{ab^3}{2(a^2+b^2)}</cmath>
 +
 +
<cmath>BF = \frac{ 2[CEB] }{BC} = \frac{ 2 \cdot \frac{ab^3}{ 2(a^2+b^2) } }{b} = \frac{ab^2}{a^2+b^2}</cmath>
 +
 +
<cmath>\because \triangle BFE \sim \triangle ABC, \quad \therefore \frac{EF}{BF} = \frac{BC}{AB}, \quad EF = BF \cdot \frac{BC}{AB} = \frac{ab^2}{a^2+b^2} \cdot \frac{b}{a} = \frac{b^3}{a^2+b^2}</cmath>
 +
 +
<cmath>EG = FG - EF = b - \frac{b^3}{a^2+b^2} = \frac{a^2b}{a^2+b^2}</cmath>
 +
 +
<cmath>[ABCD] = \frac{AB + CD}{2} \cdot BC = \frac{a + \frac{b^2}{a} }{2} \cdot b = \frac{ b(a^2+b^2) }{ 2a }</cmath>
 +
 +
<cmath>[ABE] = \frac12 \cdot AB \cdot EF = \frac12 \cdot a \cdot \frac{b^3}{a^2+b^2} = \frac{ab^3}{ 2(a^2+b^2) }</cmath>
 +
 +
<cmath>[CDE] = \frac12 \cdot CD \cdot EG = \frac12 \cdot \frac{a^2b}{a^2+b^2} \cdot \frac{a^2b}{a^2+b^2} = \frac{ab^3}{ 2(a^2+b^2) }</cmath>
  
−
<math>5+9=\boxed{\textbf{(B) } 14}</math>.
+
<cmath>ADE = [ABCD] - [ABE] - [CEB] - [CDE] = \frac{ b(a^2+b^2) }{ 2a } - \frac{ab^3}{ 2(a^2+b^2) } - \frac{ab^3}{ 2(a^2+b^2) }- \frac{ab^3}{ 2(a^2+b^2) } = \frac{ b(a^2+b^2)^2 - 3a^2b^3 }{ 2a(a^2+b^2) } </cmath>
 +
 
 +
<cmath>\frac{ [ADE] }{ [CEB] } = \frac { \frac{ b(a^2+b^2)^2 - 3a^2b^3 }{ 2a(a^2+b^2) } }{ \frac{ab^3}{2(a^2+b^2)} } = \frac{
 +
(a^2 + b^2)^2 - 3a^2b^2 }{ a^2b^2 } = \frac{ a^4 - a^2b^2 + b^4 }{ a^2b^2 } = 17</cmath>
 +
 
 +
<cmath>a^4 - a^2b^2 + b^4 = 17 a^2b^2, \quad a^4 + b^4 = 18 a^2b^2, \quad \frac{a^2}{b^2} + \frac{b^2}{a^2} = 18</cmath>
 +
 
 +
Let <math>x = \frac{a}{b}</math>,
 +
 
 +
<cmath>x^2 + \frac{1}{x^2} = 18, \quad x^4 - 18x^2 + 1 = 0, \quad x^2 = \frac{18 + \sqrt{324-4} }{2} = 9+ 4\sqrt{5}</cmath>
 +
 
 +
<cmath>\frac{a}{b} = \sqrt{ 9+ 4\sqrt{5} } = \sqrt{ 4+ 4\sqrt{5}+5 } = \boxed{\textbf{(D) } 2+ \sqrt{5}}</cmath>
  
 
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
 
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
Line 61: Line 90:
  
 
~Zeric
 
~Zeric
 +
 +
==Solution 6==
 +
 +
This solution involves proving <math>\triangle AED \sim \triangle CEB</math>.
 +
 +
Let <math>E'</math> be the intersection of <math>AC</math> and <math>BD</math>. Label points <math>F</math> and <math>G</math> the same way as <math>\textbf{Solution 3}</math>.
 +
 +
 +
<math>\angle AE'D = \angle CE'B = \frac{\pi}{2} = \angle AFE</math>. Additionally, <math>\frac{E'D}{FE} = \frac{E'D}{E'G} = \frac{AE'}{AF}</math>, so <math>\triangle AFE \sim \triangle AE'D</math> by SAS. Therefore, <math>\angle BAC = \angle FAE + \angle EAE' = \angle E'AD + \angle EAE' = \angle EAD</math>.
 +
 +
 +
Next, <math>\angle AFE = \frac{\pi}{2} = \angle EGD</math> because <math>FG \parallel BC</math>. Also, <math>\pi = \angle FEA + \angle AED + \angle DEG = \angle FEA + \angle AED + \angle EAF = \frac{\pi}{2} + \angle AED</math>, so <math>\angle AED = \frac{\pi}{2}</math>. Therefore, <math>\triangle AED \sim \triangle ABC</math> by AA. Since <math>\triangle CEB \sim \triangle ABC</math>, <math>\triangle AED \sim \triangle CEB</math>.
 +
 +
 +
Given <math>\frac{[AED]}{[CEB]} = 17</math>, we deduce that the ratio of corresponding side lengths of <math>AED</math> to <math>CEB</math> must be <math>\sqrt{17}</math>. Now, we set <math>BC = 1</math>, <math>AB = x</math>, and <math>CD = \frac{1}{x}</math>. Using the Pythagorean Theorem, <math>AD = \sqrt{\Big(x-\frac{1}{x}\Big)^2 + 1^2}</math>. Thus, <math>\sqrt{17} = \frac{AD}{CB} = \frac{\sqrt{\Big(x-\frac{1}{x}\Big)^2 + 1^2}}{1}</math>. Solving gives <math>x = 2+\sqrt{5}</math>.
 +
 +
 +
Finally, <math>\frac{AB}{BC} = \frac{2+\sqrt{5}}{1} = \boxed{\textbf{(D) } 2+\sqrt{5}}</math>.
 +
 +
~Zhixing
  
 
==Video Solution by MOP 2024==
 
==Video Solution by MOP 2024==

Latest revision as of 17:06, 31 July 2024

Problem

Quadrilateral $ABCD$ has right angles at $B$ and $C$, $\triangle ABC \sim \triangle BCD$, and $AB > BC$. There is a point $E$ in the interior of $ABCD$ such that $\triangle ABC \sim \triangle CEB$ and the area of $\triangle AED$ is $17$ times the area of $\triangle CEB$. What is $\tfrac{AB}{BC}$?

$\textbf{(A) } 1+\sqrt{2} \qquad \textbf{(B) } 2 + \sqrt{2} \qquad \textbf{(C) } \sqrt{17} \qquad \textbf{(D) } 2 + \sqrt{5} \qquad \textbf{(E) } 1 + 2\sqrt{3}$

Solution 1

Let $CD=1$, $BC=x$, and $AB=x^2$. Note that $AB/BC=x$. By the Pythagorean Theorem, $BD=\sqrt{x^2+1}$. Since $\triangle BCD \sim \triangle ABC \sim \triangle CEB$, the ratios of side lengths must be equal. Since $BC=x$, $CE=\frac{x^2}{\sqrt{x^2+1}}$ and $BE=\frac{x}{\sqrt{x^2+1}}$. Let F be a point on $\overline{BC}$ such that $\overline{EF}$ is an altitude of triangle $CEB$. Note that $\triangle CEB \sim \triangle CFE \sim \triangle EFB$. Therefore, $BF=\frac{x}{x^2+1}$ and $CF=\frac{x^3}{x^2+1}$. Since $\overline{CF}$ and $\overline{BF}$ form altitudes of triangles $CED$ and $BEA$, respectively, the areas of these triangles can be calculated. Additionally, the area of triangle $BEC$ can be calculated, as it is a right triangle. Solving for each of these yields:

\begin{align*} [BEC] &=[CED]=[BEA]=\frac{x^3}{2(x^2+1)} \\ [ABCD] &=[AED]+[DEC]+[CEB]+[BEA] \\ \frac{(BC)(AB+CD)}{2} &= 17*[CEB]+ [CEB] + [CEB] + [CEB] \\ \frac{x^3+x}{2} &= \frac{20x^3}{2(x^2+1)} \\ \frac{x}{x^2+1} &= \frac{20x^3}{x^2+1} \\ (x^2+1)^2 &=20x^2 \\ x^4-18x^2+1 &=0 \implies x^2=9+4\sqrt{5}=4+2(2\sqrt{5})+5 \\ \end{align*}

Therefore, the answer is $\boxed{\textbf{(D) } 2+\sqrt{5}}$

Solution 2

Draw line $FG$ through $E$, with $F$ on $BC$ and $G$ on $AD$, $FG \parallel AB$. WLOG let $CD=1$, $CB=x$, $AB=x^2$. By weighted average $FG=\frac{1+x^4}{1+x^2}$.

Meanwhile, $FE:EG=[\triangle CBE]:[\triangle ADE]=1:17$. This follows from comparing the ratios of triangle DEG to CFE and triangle AEG to FEB, both pairs in which the two triangles share a height perpendicular to FG, and have base ratio $EG:FE$.

$FE=\frac{x^2}{1+x^2}$. We obtain $\frac{1+x^4}{1+x^2}=\frac{18x^2}{1+x^2}$, namely $x^4-18x^2+1=0$.

The rest is the same as Solution 1.

Solution 3

2017AMC12BP24.png

Let $AB = a$, $BC = b$, $AC = \sqrt{a^2+b^2}$

Note that $E$ cannot be the intersection of $AC$ and $BD$, as that would mean $[AED] = [CEB]$

\[\because \triangle BCD \sim \triangle ABC, \quad \therefore \frac{CD}{BC} = \frac{BC}{AB}, \quad CD = BC \cdot \frac{BC}{AB} = b \cdot \frac{b}{a} = \frac{b^2}{a}\]

\[[CEB] = ( \frac{BC}{AC} )^2 \cdot [ABC] = ( \frac{b}{ \sqrt{a^2+b^2} } )^2 \cdot \frac{ab}{2} = \frac{ab^3}{2(a^2+b^2)}\]

\[BF = \frac{ 2[CEB] }{BC} = \frac{ 2 \cdot \frac{ab^3}{ 2(a^2+b^2) } }{b} = \frac{ab^2}{a^2+b^2}\]

\[\because \triangle BFE \sim \triangle ABC, \quad \therefore \frac{EF}{BF} = \frac{BC}{AB}, \quad EF = BF \cdot \frac{BC}{AB} = \frac{ab^2}{a^2+b^2} \cdot \frac{b}{a} = \frac{b^3}{a^2+b^2}\]

\[EG = FG - EF = b - \frac{b^3}{a^2+b^2} = \frac{a^2b}{a^2+b^2}\]

\[[ABCD] = \frac{AB + CD}{2} \cdot BC = \frac{a + \frac{b^2}{a} }{2} \cdot b = \frac{ b(a^2+b^2) }{ 2a }\]

\[[ABE] = \frac12 \cdot AB \cdot EF = \frac12 \cdot a \cdot \frac{b^3}{a^2+b^2} = \frac{ab^3}{ 2(a^2+b^2) }\]

\[[CDE] = \frac12 \cdot CD \cdot EG = \frac12 \cdot \frac{a^2b}{a^2+b^2} \cdot \frac{a^2b}{a^2+b^2} = \frac{ab^3}{ 2(a^2+b^2) }\]

\[ADE = [ABCD] - [ABE] - [CEB] - [CDE] = \frac{ b(a^2+b^2) }{ 2a } - \frac{ab^3}{ 2(a^2+b^2) } - \frac{ab^3}{ 2(a^2+b^2) }- \frac{ab^3}{ 2(a^2+b^2) } = \frac{ b(a^2+b^2)^2 - 3a^2b^3 }{ 2a(a^2+b^2) }\]

\[\frac{ [ADE] }{ [CEB] } = \frac { \frac{ b(a^2+b^2)^2 - 3a^2b^3 }{ 2a(a^2+b^2) } }{ \frac{ab^3}{2(a^2+b^2)} } = \frac{ (a^2 + b^2)^2 - 3a^2b^2 }{ a^2b^2 } = \frac{ a^4 - a^2b^2 + b^4 }{ a^2b^2 } = 17\]

\[a^4 - a^2b^2 + b^4 = 17 a^2b^2, \quad a^4 + b^4 = 18 a^2b^2, \quad \frac{a^2}{b^2} + \frac{b^2}{a^2} = 18\]

Let $x = \frac{a}{b}$,

\[x^2 + \frac{1}{x^2} = 18, \quad x^4 - 18x^2 + 1 = 0, \quad x^2 = \frac{18 + \sqrt{324-4} }{2} = 9+ 4\sqrt{5}\]

\[\frac{a}{b} = \sqrt{ 9+ 4\sqrt{5} } = \sqrt{ 4+ 4\sqrt{5}+5 } = \boxed{\textbf{(D) } 2+ \sqrt{5}}\]

~isabelchen

Solution 4

Let $A=(-1,4a), B=(-1,0), C=(1,0), D=\bigg(1,\frac{1}{a}\bigg)$. Then from the similar triangles condition, we compute $CE=\frac{4a}{\sqrt{4a^2+1}}$ and $BE=\frac{2}{\sqrt{4a^2+1}}$. Hence, the $y$-coordinate of $E$ is just $\frac{BE\cdot CE}{BC}=\frac{4a}{4a^2+1}$. Since $E$ lies on the unit circle, we can compute the $x$ coordinate as $\frac{1-4a^2}{4a^2+1}$. By Shoelace, we want \[\frac{1}{2}\det\begin{bmatrix} -1 & 4a & 1\\ \frac{1-4a^2}{4a^2+1} & \frac{4a}{4a^2+1} & 1\\ 1 & \frac{1}{a} & 1 \end{bmatrix}=17\cdot\frac{1}{2}\cdot 2 \cdot \frac{4a}{4a^2+1}\]Factoring out denominators and expanding by minors, this is equivalent to \[\frac{32a^4-8a^2+2}{2a(4a^2+1)}=\frac{68a}{4a^2+1} \Longrightarrow 16a^4-72a^2+1=0\]This factors as $(4a^2-8a-1)(4a^2+8a-1)=0$, so $a=1+\frac{\sqrt{5}}{2}$ and so the answer is $\textbf{(D) \ }$.

Solution 5

Let $C = (0,0), D=(\frac1a, 0), B = (0,1), A = (a,1)$ where $a>1$. Because $BC = 1, a = \frac{AB}{BC}$. Notice that the diagonals are perpendicular with slopes of $\frac1a$ and $-a$. Let the intersection of $AC$ and $BD$ be $F$, then $\triangle BFC \sim \triangle ABC$. However, because $ABCD$ is a trapezoid, $\triangle$$BCF$ and $\triangle ADF$ share the same area, therefore $\triangle$$BCE$ is the reflection of $\triangle$$BCF$ over the perpendicular bisector of $BC$, which is $y=\frac12$. We use the linear equations of the diagonals, $y = -ax + 1, y = \frac1a x$, to find the coordinates of $F$. \[-ax+1 = \frac1ax \Longrightarrow x = \frac{1}{a+\frac1a} = \frac{a}{a^2+1}\] \[y = \frac1ax = \frac{1}{a^2+1}\] The y-coordinate of $E$ is simply $1-\frac{1}{a^2+1} = \frac{a^2}{a^2+1}$ The area of $\triangle BCE$ is $\frac12 \frac{a}{a^2+1}$. We apply shoelace theorem to solve for the area of $\triangle ADE$. The coordinates of the triangle are $\{(\frac{a}{a^2+1}, \frac{a^2}{a^2+1}), (a,1), (\frac1a, 0)\}$, so the area is

\[\frac12 |\frac{a^3}{a^2+1} + \frac1a - \frac{a}{a^2+1} - \frac{a}{a^2+1}| = \frac12 |\frac{a^3-2a}{a^2+1} + \frac1a|\] \[= \frac12 |\frac{a^4-2a^2}{a(a^2+1)} + \frac{a^2+1}{a(a^2+1)}| = \frac12 \frac{a^4-a^2+1}{a(a^2+1)}\] Finally, we use the property that the ratio of areas equals $17$ \[\frac{\frac12}{\frac12} \frac{\frac{a^4-a^2+1}{a(a^2+1)}}{\frac{a}{a^2+1}} = 17 \Rightarrow \frac{a^4-a^2+1}{a^2} = 17 \Rightarrow a^4-18a^2+1 = 0\] \[a^2 = 9+4\sqrt{5} = (2+\sqrt{5})^2 \Longrightarrow a = \boxed{\textbf{(D) } 2+\sqrt{5}}\]

~Zeric

Solution 6

This solution involves proving $\triangle AED \sim \triangle CEB$.

Let $E'$ be the intersection of $AC$ and $BD$. Label points $F$ and $G$ the same way as $\textbf{Solution 3}$.


$\angle AE'D = \angle CE'B = \frac{\pi}{2} = \angle AFE$. Additionally, $\frac{E'D}{FE} = \frac{E'D}{E'G} = \frac{AE'}{AF}$, so $\triangle AFE \sim \triangle AE'D$ by SAS. Therefore, $\angle BAC = \angle FAE + \angle EAE' = \angle E'AD + \angle EAE' = \angle EAD$.


Next, $\angle AFE = \frac{\pi}{2} = \angle EGD$ because $FG \parallel BC$. Also, $\pi = \angle FEA + \angle AED + \angle DEG = \angle FEA + \angle AED + \angle EAF = \frac{\pi}{2} + \angle AED$, so $\angle AED = \frac{\pi}{2}$. Therefore, $\triangle AED \sim \triangle ABC$ by AA. Since $\triangle CEB \sim \triangle ABC$, $\triangle AED \sim \triangle CEB$.


Given $\frac{[AED]}{[CEB]} = 17$, we deduce that the ratio of corresponding side lengths of $AED$ to $CEB$ must be $\sqrt{17}$. Now, we set $BC = 1$, $AB = x$, and $CD = \frac{1}{x}$. Using the Pythagorean Theorem, $AD = \sqrt{\Big(x-\frac{1}{x}\Big)^2 + 1^2}$. Thus, $\sqrt{17} = \frac{AD}{CB} = \frac{\sqrt{\Big(x-\frac{1}{x}\Big)^2 + 1^2}}{1}$. Solving gives $x = 2+\sqrt{5}$.


Finally, $\frac{AB}{BC} = \frac{2+\sqrt{5}}{1} = \boxed{\textbf{(D) } 2+\sqrt{5}}$.

~Zhixing

Video Solution by MOP 2024

https://youtu.be/h92s2BxlohI

~r00tsOfUnity

Notes

1) $\sqrt{17}$ is the most relevant answer choice because it shares numbers with the givens of the problem.

2) It's a very good guess to replace finding the area of triangle AED with the area of the triangle DAF, where F is the projection of D onto AB(then find the closest answer choice).

See Also

2017 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 23 		Followed by
Problem 25
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2017_AMC_12B_Problems/Problem_24&oldid=224084"