Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 AMC 12A Problems/Problem 17"
(→‎Solution 7 (Triogeometry))
 
(90 intermediate revisions by 26 users not shown)
Line 1: Line 1:
 +
{{duplicate|[[2021 AMC 10A Problems/Problem 17|2021 AMC 10A #17]] and [[2021 AMC 12A Problems/Problem 17|2021 AMC 12A #17]]}}
 +
 
==Problem==
 
==Problem==
−
Trapezoid <math>ABCD</math> has <math>\overline{AB}\parallel\overline{CD},BC=CD=43</math>, and <math>\overline{AD}\perp\overline{BD}</math>. Let <math>O</math> be the intersection of the diagonals <math>\overline{AC}</math> and <math>\overline{BD}</math>, and let <math>P</math> be the midpoint of <math>\overline{BD}</math>. Given that <math>OP=11</math>, the length of <math>AD</math> can be written in the form <math>m\sqrt{n}</math>, where <math>m</math> and <math>n</math> are positive integers and <math>n</math> is not divisible by the quare of any prime. What is <math>m+n</math>?
+
Trapezoid <math>ABCD</math> has <math>\overline{AB}\parallel\overline{CD},BC=CD=43</math>, and <math>\overline{AD}\perp\overline{BD}</math>. Let <math>O</math> be the intersection of the diagonals <math>\overline{AC}</math> and <math>\overline{BD}</math>, and let <math>P</math> be the midpoint of <math>\overline{BD}</math>. Given that <math>OP=11</math>, the length of <math>AD</math> can be written in the form <math>m\sqrt{n}</math>, where <math>m</math> and <math>n</math> are positive integers and <math>n</math> is not divisible by the square of any prime. What is <math>m+n</math>?
  
 
<math>\textbf{(A) }65 \qquad \textbf{(B) }132 \qquad \textbf{(C) }157 \qquad \textbf{(D) }194\qquad \textbf{(E) }215</math>
 
<math>\textbf{(A) }65 \qquad \textbf{(B) }132 \qquad \textbf{(C) }157 \qquad \textbf{(D) }194\qquad \textbf{(E) }215</math>
  
−
==Solution==
+
==Diagram==
−
{{solution}}
+
<asy>
 +
/* Made by MRENTHUSIASM */
 +
size(300);
 +
pair A, B, C, D, O, P;
 +
C = (43,0);
 +
D = (0,0);
 +
B = intersectionpoints(Circle(C,43),Circle(D,66))[0];
 +
A = intersectionpoints(Circle(D,4*sqrt(190)),B--B+100*dir(180))[1];
 +
P = midpoint(B--D);
 +
O = intersectionpoint(A--C,B--D);
 +
dot("$C$",C,1.5*SE,linewidth(4));
 +
dot("$D$",D,1.5*SW,linewidth(4));
 +
dot("$B$",B,1.5*NE,linewidth(4));
 +
dot("$A$",A,1.5*NW,linewidth(4));
 +
dot("$P$",P,1.5*N,linewidth(4));
 +
dot("$O$",O,1.5*S,linewidth(4));
 +
markscalefactor=0.25;
 +
draw(rightanglemark(A,D,O),red);
 +
draw(A--B--C--D--cycle^^A--C^^B--D^^C--P);
 +
label("$43$",B--C,E);
 +
label("$43$",C--D,S);
 +
label("$11$",midpoint(O--P),NW);
 +
</asy>
 +
~MRENTHUSIASM
 +
 
 +
== Solution 1 (Similar Triangles and Pythagorean Theorem) ==
 +
Angle chasing* reveals that <math>\triangle BPC\sim\triangle BDA</math>, therefore
 +
<cmath>2=\frac{BD}{BP}=\frac{AB}{BC}=\frac{AB}{43},</cmath>
 +
or <math>AB=86</math>.
 +
 
 +
Additional angle chasing shows that <math>\triangle ABO\sim\triangle CDO</math>, therefore
 +
<cmath>2=\frac{AB}{CD}=\frac{BO}{OD}=\frac{BP+11}{BP-11},</cmath>
 +
or <math>BP=33</math> and <math>BD=66</math>.
 +
 
 +
Since <math>\triangle ADB</math> is right, the Pythagorean theorem implies that
 +
<cmath>AD=\sqrt{86^2-66^2}=4\sqrt{190}.</cmath>
 +
The answer is <math>4+190=\boxed{\textbf{(D) }194}</math>.
 +
 
 +
* Angle Chasing: If we set <math>\angle DBC = \alpha</math>, then we know that <math>\angle DCB = 180^\circ-2\alpha</math> because <math>\triangle DBC</math> is isosceles. Then, <math>\angle BCP = 90^\circ-\alpha</math>, so <math>\angle BPC</math> is a right angle. Because <math>\angle BDC = \alpha</math> and <math>\overline{AB}\parallel\overline{DC}</math>, we conclude that <math>\angle ABD = \alpha</math> too. Lastly, because <math>\triangle BPC</math> and <math>\triangle BDA</math> are both right triangles, they are similar by AA.
 +
 
 +
~mn28407 (Solution)
 +
 
 +
~mm (Angle Chasing Remark)
 +
 
 +
~eagleye ~MRENTHUSIASM ~charyyu83 (Minor Edits)
 +
 
 +
==Solution 2 (Similar Triangles, Areas, Pythagorean Theorem)==
 +
Since <math>\triangle BCD</math> is isosceles with base <math>\overline{BD},</math> it follows that median <math>\overline{CP}</math> is also an altitude. Let <math>OD=x</math> and <math>CP=h,</math> so <math>PB=x+11.</math>
 +
 
 +
Since <math>\angle AOD=\angle COP</math> by vertical angles, we conclude that <math>\triangle AOD\sim\triangle COP</math> by AA, from which <math>\frac{AD}{CP}=\frac{OD}{OP},</math> or <cmath>AD=CP\cdot\frac{OD}{OP}=h\cdot\frac{x}{11}.</cmath> Let the brackets denote areas. Notice that <math>[AOD]=[BOC]</math> (By the same base and height, we deduce that <math>[ACD]=[BDC].</math> Subtracting <math>[OCD]</math> from both sides gives <math>[AOD]=[BOC].</math>). Doubling both sides produces
 +
<cmath>\begin{align*}
 +
2[AOD]&=2[BOC] \\
 +
OD\cdot AD&=OB\cdot CP \\
 +
x\left(\frac{hx}{11}\right)&=(x+22)h \\
 +
x^2&=11(x+22).
 +
\end{align*}</cmath>
 +
Rearranging and factoring result in <math>(x-22)(x+11)=0,</math> from which <math>x=22.</math>
 +
 
 +
Applying the Pythagorean Theorem to right <math>\triangle CPB,</math> we have <cmath>h=\sqrt{43^2-33^2}=\sqrt{(43+33)(43-33)}=\sqrt{760}=2\sqrt{190}.</cmath> Finally, we get <cmath>AD=h\cdot\frac{x}{11}=4\sqrt{190},</cmath> so the answer is <math>4+190=\boxed{\textbf{(D) }194}.</math>
 +
 
 +
~MRENTHUSIASM
 +
 
 +
==Solution 3 (Short)==
 +
Let <math>CP = y</math>. <math>CP</math> a is perpendicular bisector of <math>DB.</math> Then, let <math>DO = x,</math> thus <math>DP = PB = 11+x.</math>
 +
 
 +
(1) <math>\triangle CPO \sim \triangle ADO,</math> so we get <math>\frac{AD}{x} = \frac{y}{11},</math> or <math>AD = \frac{xy}{11}.</math>
 +
 
 +
(2) Applying Pythagorean Theorem on <math>\triangle CDP</math> gives <math>(11+x)^2 + y^2 = 43^2.</math>
 +
 
 +
(3) <math>\triangle BPC \sim \triangle BDA</math> with ratio <math>1:2,</math> so <math>AD = 2y</math> using the fact that <math>P</math> is the midpoint of <math>BD</math>.
 +
 
 +
Thus, <math>\frac{xy}{11} = 2y,</math> or <math>x = 22.</math> And <math>y = \sqrt{43^2 - 33^2} = 2 \sqrt{190},</math> so <math>AD = 4 \sqrt{190}</math> and the answer is <math>4+190=\boxed{\textbf{(D) }194}.</math>
 +
 
 +
~ ccx09
 +
 
 +
==Solution 4 (Extending the Line)==
 +
Observe that <math>\triangle BPC</math> is congruent to <math>\triangle DPC</math>; both are similar to <math>\triangle BDA</math>. Let's extend <math>\overline{AD}</math> and <math>\overline{BC}</math> past points <math>D</math> and <math>C</math> respectively, such that they intersect at a point <math>E</math>. Observe that <math>\angle BDE</math> is <math>90</math> degrees, and that <math>\angle DBE \cong \angle PBC \cong \angle DBA \implies \angle DBE \cong \angle DBA</math>. Thus, by ASA, we know that <math>\triangle ABD \cong \triangle EBD</math>, thus, <math>AD = ED</math>, meaning <math>D</math> is the midpoint of <math>AE</math>.
 +
Let <math>M</math> be the midpoint of <math>\overline{DE}</math>. Note that <math>\triangle CME</math> is congruent to <math>\triangle BPC</math>, thus <math>BC = CE</math>, meaning <math>C</math> is the midpoint of <math>\overline{BE}.</math>
 +
 
 +
Therefore, <math>\overline{AC}</math> and <math>\overline{BD}</math> are both medians of <math>\triangle ABE</math>. This means that <math>O</math> is the centroid of <math>\triangle ABE</math>; therefore, because the centroid divides the median in a 2:1 ratio, <math>\frac{BO}{2} = DO = \frac{BD}{3}</math>. Recall that <math>P</math> is the midpoint of <math>BD</math>; <math>DP = \frac{BD}{2}</math>. The question tells us that <math>OP = 11</math>; <math>DP-DO=11</math>; we can write this in terms of <math>DB</math>; <math>\frac{DB}{2}-\frac{DB}{3} = \frac{DB}{6} = 11 \implies DB = 66</math>.
 +
 
 +
We are almost finished. Each side length of <math>\triangle ABD</math> is twice as long as the corresponding side length <math>\triangle CBP</math> or <math>\triangle CPD</math>, since those triangles are similar; this means that <math>AB = 2 \cdot 43 = 86</math>. Now, by Pythagorean theorem on <math>\triangle ABD</math>, <math>AB^{2} - BD^{2} = AD^{2} \implies 86^{2}-66^{2} = AD^{2} \implies AD = \sqrt{3040} \implies AD = 4 \sqrt{190}</math>.
 +
 
 +
The answer is <math>4+190 = \boxed{\textbf{(D) }194}</math>.
 +
 
 +
~ihatemath123
 +
 
 +
==Solution 5==
 +
Since <math>P</math> is the midpoint of isosceles triangle <math>BCD</math>, it would be pretty easy to see that <math>CP\perp BD</math>. Since <math>AD\perp BD</math> as well, <math>AD\parallel CP</math>. Connecting <math>AP</math>, it’s obvious that <math>[ADC]=[ADP]</math>. Since <math>DP=BP</math>, <math>[APB]=[ADC]</math>.
 +
 
 +
Since <math>P</math> is the midpoint of <math>BD</math>, the height of <math>\triangle APB</math> on side <math>AB</math> is half that of <math>\triangle ADC</math> on <math>CD</math>. Since <math>[APB]=[ADC]</math>, <math>AB=2CD</math>.
 +
 
 +
As a basic property of a trapezoid, <math>\triangle AOB \sim \triangle COD</math>, so <math>\frac{OB}{OD}=\frac{AB}{CD}=2</math>, or <math>OB=2OD</math>. Letting <math>OD=x</math>, then <math>PB=DP=11+x</math>, and <math>OB=22+x</math>. Hence <math>22+x=2x</math> and <math>x=22</math>.
 +
 
 +
Since <math>\triangle AOD \sim \triangle COP</math>, <math>\frac{AD}{PC}=\frac{OD}{OP}=2</math>. Since <math>PD=11+22=33</math>, <math>PC=\sqrt{43^2-33^2}=\sqrt{760}</math>.
 +
 
 +
So, <math>AD=2\sqrt{760}=4\sqrt{190}</math>. The correct answer is <math>\boxed{\textbf{(D) }194}</math>.
 +
 
 +
==Solution 6 (Coordinate Geometry) ==
 +
 
 +
Let <math>D</math> be the origin of the cartesian coordinate plane, <math>B</math> lie on the positive <math>x</math>-axis, and <math>A</math> lie on the negative <math>y</math>-axis. Then let the coordinates of <math>B = (2a,0), A = (0, -2b).</math> Then the slope of <math>AB</math> is <math>\frac{b}{a}.</math> Since <math>AB \parallel CD</math> the slope of <math>CD</math> is the same. Note that as <math>\triangle DCB</math> is isosceles <math>C</math> lies on <math>x = a.</math> Thus since <math>CD</math> has equation <math>y = \frac{b}{a}x</math> (<math>D</math> is the origin), <math>C = (a,b).</math> Therefore <math>AC</math> has equation <math>y = \frac{3b}{a}x - 2b</math> and intersects <math>BD</math> (<math>x</math>-axis) at <math>O =\left(\frac{2}{3}a, 0\right).</math> The midpoint of <math>BD</math> is <math>P = (a,0),</math> so <math>OP = \frac{a}{3} = 11,</math> from which <math>a = 33.</math> Then by Pythagorean theorem on <math>\triangle DPC</math> (<math>\triangle DBC</math> is isosceles), we have <math>b = \sqrt{43^2 - 33^2} = 2\sqrt{190},</math> so <math>2b=4\sqrt{190}.</math>
 +
 
 +
Finally, the answer is <math>4+190=\boxed{\textbf{(D) }194}.</math>
 +
 
 +
~Aaryabhatta1
 +
 
 +
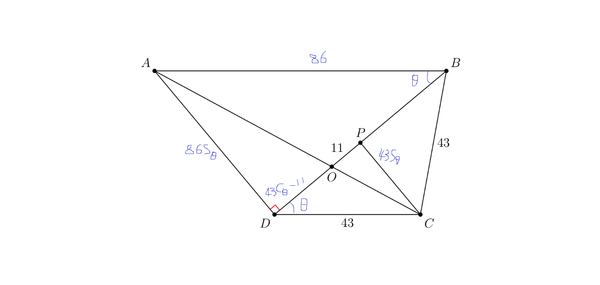
==Solution 7 (Trigonometry) ==
 +
 
 +
[[Image:2021_12A_p17.png|thumb|center|600px|]]
 +
 
 +
set <math>\angle BDC  = \theta  </math>
 +
 
 +
BD = 2*DP = 2*43*Cos(<math>\theta</math>)
 +
 
 +
AB = BD / Cos（<math>\angle DBA</math>） = BD / Cos(<math>\theta</math>) =  2 *43 * Cos(<math>\theta</math>) / Cos(<math>\theta</math>) = 86
 +
 
 +
OP/DO = CP / AD
 +
 
 +
11 / (43Cos(<math>\theta</math>) - 11) = 43Sin(<math>\theta</math>) / 86 Sin(<math>\theta</math>) 
 +
 
 +
Cos(<math>\theta</math>) = 33/ 43
 +
 
 +
AD = 86 * Sin(<math>\theta</math>) = 2<math>\sqrt{760}= 4\sqrt{190}=\boxed{\textbf{(D) }194}</math>.
 +
 
 +
~[https://artofproblemsolving.com/wiki/index.php/User:Cyantist luckuso]
 +
 
 +
== Video Solution by OmegaLearn (Using Similar Triangles, Pythagorean Theorem) ==
 +
https://youtu.be/gjeSGJy_ld4
 +
 
 +
~ pi_is_3.14
 +
 
 +
==Video Solution by Punxsutawney Phil==
 +
https://youtube.com/watch?v=rtdovluzgQs
 +
 
 +
== Video Solution by Mathematical Dexterity ==
 +
https://www.youtube.com/watch?v=QzAVdsgBBqg
  
 
==See also==
 
==See also==
 +
{{AMC10 box|year=2021|ab=A|num-b=16|num-a=18}}
 
{{AMC12 box|year=2021|ab=A|num-b=16|num-a=18}}
 
{{AMC12 box|year=2021|ab=A|num-b=16|num-a=18}}
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 22:51, 23 July 2024

The following problem is from both the 2021 AMC 10A #17 and 2021 AMC 12A #17, so both problems redirect to this page.

Problem

Trapezoid $ABCD$ has $\overline{AB}\parallel\overline{CD},BC=CD=43$, and $\overline{AD}\perp\overline{BD}$. Let $O$ be the intersection of the diagonals $\overline{AC}$ and $\overline{BD}$, and let $P$ be the midpoint of $\overline{BD}$. Given that $OP=11$, the length of $AD$ can be written in the form $m\sqrt{n}$, where $m$ and $n$ are positive integers and $n$ is not divisible by the square of any prime. What is $m+n$?

$\textbf{(A) }65 \qquad \textbf{(B) }132 \qquad \textbf{(C) }157 \qquad \textbf{(D) }194\qquad \textbf{(E) }215$

Diagram

[asy] /* Made by MRENTHUSIASM */ size(300); pair A, B, C, D, O, P; C = (43,0); D = (0,0); B = intersectionpoints(Circle(C,43),Circle(D,66))[0]; A = intersectionpoints(Circle(D,4*sqrt(190)),B--B+100*dir(180))[1]; P = midpoint(B--D); O = intersectionpoint(A--C,B--D); dot("$C$",C,1.5*SE,linewidth(4)); dot("$D$",D,1.5*SW,linewidth(4)); dot("$B$",B,1.5*NE,linewidth(4)); dot("$A$",A,1.5*NW,linewidth(4)); dot("$P$",P,1.5*N,linewidth(4)); dot("$O$",O,1.5*S,linewidth(4)); markscalefactor=0.25; draw(rightanglemark(A,D,O),red); draw(A--B--C--D--cycle^^A--C^^B--D^^C--P); label("$43$",B--C,E); label("$43$",C--D,S); label("$11$",midpoint(O--P),NW); [/asy] ~MRENTHUSIASM

Solution 1 (Similar Triangles and Pythagorean Theorem)

Angle chasing* reveals that $\triangle BPC\sim\triangle BDA$, therefore \[2=\frac{BD}{BP}=\frac{AB}{BC}=\frac{AB}{43},\] or $AB=86$.

Additional angle chasing shows that $\triangle ABO\sim\triangle CDO$, therefore \[2=\frac{AB}{CD}=\frac{BO}{OD}=\frac{BP+11}{BP-11},\] or $BP=33$ and $BD=66$.

Since $\triangle ADB$ is right, the Pythagorean theorem implies that \[AD=\sqrt{86^2-66^2}=4\sqrt{190}.\] The answer is $4+190=\boxed{\textbf{(D) }194}$.

  • Angle Chasing: If we set $\angle DBC = \alpha$, then we know that $\angle DCB = 180^\circ-2\alpha$ because $\triangle DBC$ is isosceles. Then, $\angle BCP = 90^\circ-\alpha$, so $\angle BPC$ is a right angle. Because $\angle BDC = \alpha$ and $\overline{AB}\parallel\overline{DC}$, we conclude that $\angle ABD = \alpha$ too. Lastly, because $\triangle BPC$ and $\triangle BDA$ are both right triangles, they are similar by AA.

~mn28407 (Solution)

~mm (Angle Chasing Remark)

~eagleye ~MRENTHUSIASM ~charyyu83 (Minor Edits)

Solution 2 (Similar Triangles, Areas, Pythagorean Theorem)

Since $\triangle BCD$ is isosceles with base $\overline{BD},$ it follows that median $\overline{CP}$ is also an altitude. Let $OD=x$ and $CP=h,$ so $PB=x+11.$

Since $\angle AOD=\angle COP$ by vertical angles, we conclude that $\triangle AOD\sim\triangle COP$ by AA, from which $\frac{AD}{CP}=\frac{OD}{OP},$ or \[AD=CP\cdot\frac{OD}{OP}=h\cdot\frac{x}{11}.\] Let the brackets denote areas. Notice that $[AOD]=[BOC]$ (By the same base and height, we deduce that $[ACD]=[BDC].$ Subtracting $[OCD]$ from both sides gives $[AOD]=[BOC].$). Doubling both sides produces \begin{align*} 2[AOD]&=2[BOC] \\ OD\cdot AD&=OB\cdot CP \\ x\left(\frac{hx}{11}\right)&=(x+22)h \\ x^2&=11(x+22). \end{align*} Rearranging and factoring result in $(x-22)(x+11)=0,$ from which $x=22.$

Applying the Pythagorean Theorem to right $\triangle CPB,$ we have \[h=\sqrt{43^2-33^2}=\sqrt{(43+33)(43-33)}=\sqrt{760}=2\sqrt{190}.\] Finally, we get \[AD=h\cdot\frac{x}{11}=4\sqrt{190},\] so the answer is $4+190=\boxed{\textbf{(D) }194}.$

~MRENTHUSIASM

Solution 3 (Short)

Let $CP = y$. $CP$ a is perpendicular bisector of $DB.$ Then, let $DO = x,$ thus $DP = PB = 11+x.$

(1) $\triangle CPO \sim \triangle ADO,$ so we get $\frac{AD}{x} = \frac{y}{11},$ or $AD = \frac{xy}{11}.$

(2) Applying Pythagorean Theorem on $\triangle CDP$ gives $(11+x)^2 + y^2 = 43^2.$

(3) $\triangle BPC \sim \triangle BDA$ with ratio $1:2,$ so $AD = 2y$ using the fact that $P$ is the midpoint of $BD$.

Thus, $\frac{xy}{11} = 2y,$ or $x = 22.$ And $y = \sqrt{43^2 - 33^2} = 2 \sqrt{190},$ so $AD = 4 \sqrt{190}$ and the answer is $4+190=\boxed{\textbf{(D) }194}.$

~ ccx09

Solution 4 (Extending the Line)

Observe that $\triangle BPC$ is congruent to $\triangle DPC$; both are similar to $\triangle BDA$. Let's extend $\overline{AD}$ and $\overline{BC}$ past points $D$ and $C$ respectively, such that they intersect at a point $E$. Observe that $\angle BDE$ is $90$ degrees, and that $\angle DBE \cong \angle PBC \cong \angle DBA \implies \angle DBE \cong \angle DBA$. Thus, by ASA, we know that $\triangle ABD \cong \triangle EBD$, thus, $AD = ED$, meaning $D$ is the midpoint of $AE$. Let $M$ be the midpoint of $\overline{DE}$. Note that $\triangle CME$ is congruent to $\triangle BPC$, thus $BC = CE$, meaning $C$ is the midpoint of $\overline{BE}.$

Therefore, $\overline{AC}$ and $\overline{BD}$ are both medians of $\triangle ABE$. This means that $O$ is the centroid of $\triangle ABE$; therefore, because the centroid divides the median in a 2:1 ratio, $\frac{BO}{2} = DO = \frac{BD}{3}$. Recall that $P$ is the midpoint of $BD$; $DP = \frac{BD}{2}$. The question tells us that $OP = 11$; $DP-DO=11$; we can write this in terms of $DB$; $\frac{DB}{2}-\frac{DB}{3} = \frac{DB}{6} = 11 \implies DB = 66$.

We are almost finished. Each side length of $\triangle ABD$ is twice as long as the corresponding side length $\triangle CBP$ or $\triangle CPD$, since those triangles are similar; this means that $AB = 2 \cdot 43 = 86$. Now, by Pythagorean theorem on $\triangle ABD$, $AB^{2} - BD^{2} = AD^{2} \implies 86^{2}-66^{2} = AD^{2} \implies AD = \sqrt{3040} \implies AD = 4 \sqrt{190}$.

The answer is $4+190 = \boxed{\textbf{(D) }194}$.

~ihatemath123

Solution 5

Since $P$ is the midpoint of isosceles triangle $BCD$, it would be pretty easy to see that $CP\perp BD$. Since $AD\perp BD$ as well, $AD\parallel CP$. Connecting $AP$, it’s obvious that $[ADC]=[ADP]$. Since $DP=BP$, $[APB]=[ADC]$.

Since $P$ is the midpoint of $BD$, the height of $\triangle APB$ on side $AB$ is half that of $\triangle ADC$ on $CD$. Since $[APB]=[ADC]$, $AB=2CD$.

As a basic property of a trapezoid, $\triangle AOB \sim \triangle COD$, so $\frac{OB}{OD}=\frac{AB}{CD}=2$, or $OB=2OD$. Letting $OD=x$, then $PB=DP=11+x$, and $OB=22+x$. Hence $22+x=2x$ and $x=22$.

Since $\triangle AOD \sim \triangle COP$, $\frac{AD}{PC}=\frac{OD}{OP}=2$. Since $PD=11+22=33$, $PC=\sqrt{43^2-33^2}=\sqrt{760}$.

So, $AD=2\sqrt{760}=4\sqrt{190}$. The correct answer is $\boxed{\textbf{(D) }194}$.

Solution 6 (Coordinate Geometry)

Let $D$ be the origin of the cartesian coordinate plane, $B$ lie on the positive $x$-axis, and $A$ lie on the negative $y$-axis. Then let the coordinates of $B = (2a,0), A = (0, -2b).$ Then the slope of $AB$ is $\frac{b}{a}.$ Since $AB \parallel CD$ the slope of $CD$ is the same. Note that as $\triangle DCB$ is isosceles $C$ lies on $x = a.$ Thus since $CD$ has equation $y = \frac{b}{a}x$ ($D$ is the origin), $C = (a,b).$ Therefore $AC$ has equation $y = \frac{3b}{a}x - 2b$ and intersects $BD$ ($x$-axis) at $O =\left(\frac{2}{3}a, 0\right).$ The midpoint of $BD$ is $P = (a,0),$ so $OP = \frac{a}{3} = 11,$ from which $a = 33.$ Then by Pythagorean theorem on $\triangle DPC$ ($\triangle DBC$ is isosceles), we have $b = \sqrt{43^2 - 33^2} = 2\sqrt{190},$ so $2b=4\sqrt{190}.$

Finally, the answer is $4+190=\boxed{\textbf{(D) }194}.$

~Aaryabhatta1

Solution 7 (Trigonometry)

2021 12A p17.png

set $\angle BDC = \theta$

BD = 2*DP = 2*43*Cos($\theta$)

AB = BD / Cos（$\angle DBA$） = BD / Cos($\theta$) = 2 *43 * Cos($\theta$) / Cos($\theta$) = 86

OP/DO = CP / AD

11 / (43Cos($\theta$) - 11) = 43Sin($\theta$) / 86 Sin($\theta$)

Cos($\theta$) = 33/ 43

AD = 86 * Sin($\theta$) = 2$\sqrt{760}= 4\sqrt{190}=\boxed{\textbf{(D) }194}$.

~luckuso

Video Solution by OmegaLearn (Using Similar Triangles, Pythagorean Theorem)

https://youtu.be/gjeSGJy_ld4

~ pi_is_3.14

Video Solution by Punxsutawney Phil

https://youtube.com/watch?v=rtdovluzgQs

Video Solution by Mathematical Dexterity

https://www.youtube.com/watch?v=QzAVdsgBBqg

See also

2021 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 16 		Followed by
Problem 18
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions
2021 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 16 		Followed by
Problem 18
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_AMC_12A_Problems/Problem_17&oldid=223476"