Difference between revisions of "Discriminant"

Latest revision as of 16:56, 24 June 2024

The discriminant of a quadratic equation of the form $a{x}^2+b{x}+{c}=0$ is the quantity $b^2-4ac$ . When ${a},{b},{c}$ are real, this is a notable quantity, because if the discriminant is positive, the equation has two real roots; if the discriminant is negative, the equation has two nonreal roots; and if the discriminant is 0, the equation has a real double root.

Discriminant of polynomials of degree n

The discriminant can tell us something about the roots of a given polynomial $p(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_0$ of degree $n$ with all the coefficients being real. But for polynomials of degree 4 or higher it can be difficult to use it.

General formula of discriminant

We know that the discriminant of a polynomial is the product of the squares of the differences of the polynomial roots $r_i$ , so,

$D(p)=a_n^{2n-2}\prod_{i<j}^{n}(r_i-r_j)^2$

When $n=2$

Given a polynomial $p(x)=ax^2+bx+c$ , its discriminant is $D(p)=b^2-4ac$ , which can also be denoted by $\Delta=b^2-4ac$ .

For $\Delta>0$ we have the graph

which has two distinct real roots.

For $\Delta<0$ we have the graph

which has two non-real roots.

And for the case $\Delta=0$ ,

When $n=3$

The discriminant of a polynomial $p(x)=ax^3+bx^2+cx+d$ is given by $D(p)=b^2c^2-4b^3d-4ac^3+18abcd-27a^2d^2$ .

Also, the depressed cubic form $p(z)=z^3+pz+q$ has discriminant $D(p)=-4p^3-27q^2$ . We can compress a polynomial of degree 3, which also makes possible to us to use Cardano's formula, by doing the substitution $x=z-\frac{a}{3}$ on the polynomial $p(x)=x^3+ax^2+bx+c$ .

If $D=0$ , then at least two of the roots are equal;

If $D<0$ , then all three roots are real and distinct;

If $D>0$ , then one of the roots is real and the other two are complex conjugate.

When $n=4$

The quartic polynomial $p(x)=ax^4+bx^3+cx^2+dx+e$ has discriminant

$D(p)=256a^3e^3-192a^2bde^2-128a^2c^2e^2+144a^2cd^2e-27a^2d^4+144ab^2ce^2-6ab^2d^2e-80abc^2de+18abcd^3+16ac^4e-4ac^3d^2-27b^4e^2+18b^3cde-4b^3d^3-4b^2c^3e+b^2c^2d^2$

If $D=0$ , then at least two of the roots are equal;
If $D>0$ , then the roots are all real or all non-real;
If $D<0$ , then there are two real roots and two complex conjugate roots.

Some properties

For $n\geq4$ we can say that

The polynomial has a multiple root if, and only if, $D=0$ ;
If $D>0$ , with $k$ being a positive integer such that $k\geq\frac{n}{4}$ , with $n$ being the degree of the polynomial, then there are $2k$ pairs of complex conjugate roots and $n-4k$ real roots;
If $D<0$ , with $k$ being a positive integer such that $k\geq\frac{n-2}{4}$ , then there are $2k+1$ pairs of complex conjugate roots and $n-4k+2$ real roots.

Example Problems

Introductory

(AMC 12 2005) There are two values of $a$ for which the equation $4x^2+ax+8x+9=0$ has only one solution for $x$ . What is the sum of these values of $a$ ?

Solution: Since we want the $a$ 's where there is only one solution for $x$ , the discriminant has to be $0$ . $(a+8)^2-4(4)(9)=a^2+16a-80=0$ . The sum of these values of $a$ is $-16$ .

Intermediate

1977 Canadian MO Problem 1

Other resources

Wikipedia entry

@@ Line 1: / Line 1: @@
-The '''discriminant''' of a [[Quadratic Equations | Quadratic Equation]] of the form <math>ax^2+bx+c=0</math> is the quantity <math>b^2-4ac</math>.  When <math>a</math>, <math>b</math>, and <math>c</math> are real, this is a notable quantity, because if the Discriminant is positive, the equation has two real [[Roots | roots]]; if the discriminant is negative, the equation has two non-real roots; and if the discriminant is 0, the equation has a real [[Double Root | double root]].
+The '''discriminant''' of a [[quadratic equation]] of the form <math>a{x}^2+b{x}+{c}=0</math> is the quantity <math>b^2-4ac</math>.  When <math>{a},{b},{c}</math> are real, this is a notable quantity, because if the discriminant is positive, the equation has two [[real]] [[root]]s; if the discriminant is negative, the equation has two [[nonreal]] roots; and if the discriminant is 0, the equation has a real [[double root]].
+==Discriminant of polynomials of degree n==
+The discriminant can tell us something about the roots of a given [[polynomial]] <math>p(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_0</math> of degree <math>n</math> with all the coefficients being real. But for polynomials of degree 4 or higher it can be difficult to use it.
+===General formula of discriminant===
+We know that the discriminant of a polynomial is the product of the squares of the differences of the polynomial roots <math>r_i</math>, so,
+<math>D(p)=a_n^{2n-2}\prod_{i<j}^{n}(r_i-r_j)^2</math>
+====When <math>n=2</math>====
+Given a polynomial <math>p(x)=ax^2+bx+c</math>, its discriminant is <math>D(p)=b^2-4ac</math>, which can also be denoted by <math>\Delta=b^2-4ac</math>.
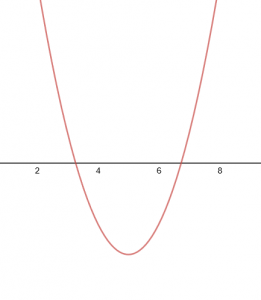
+For <math>\Delta>0</math> we have the graph
+[[Image:Delta_greater_than_0.png|thumb|center|300x300px]]
+which has two distinct real roots.
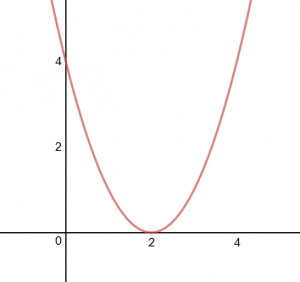
+For <math>\Delta<0</math> we have the graph
+[[File:Delta_lower_than_0.png|thumb|center|300x300px]]
+which has two non-real roots.
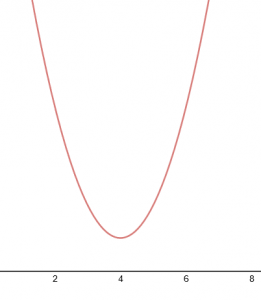
+And for the case <math>\Delta=0</math>,
+[[Image:Delta_equal_to_0.png|thumb|center|300x300px]]
+====When <math>n=3</math>====
+The discriminant of a polynomial <math>p(x)=ax^3+bx^2+cx+d</math> is given by <math>D(p)=b^2c^2-4b^3d-4ac^3+18abcd-27a^2d^2</math>.
+Also, the depressed [[cubic Equation|cubic]] form <math>p(z)=z^3+pz+q</math> has discriminant <math>D(p)=-4p^3-27q^2</math>. We can compress a polynomial of degree 3, which also makes possible to us to use Cardano's formula, by doing the substitution <math>x=z-\frac{a}{3}</math> on the polynomial <math>p(x)=x^3+ax^2+bx+c</math>.
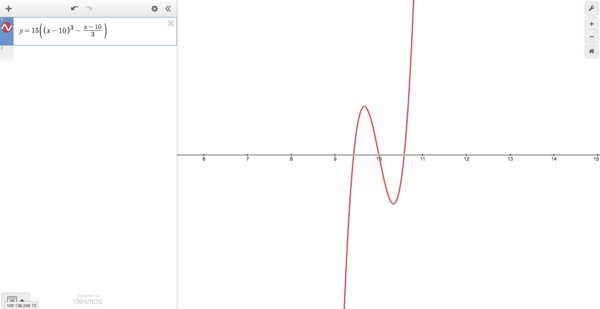
+*If <math>D=0</math>, then at least two of the roots are equal;
+[[Image:Cubic delta=0 01.png|thumb|center|600x600px]]
+[[Image:Cubic delta=0 02.png|thumb|center|600x600px]]
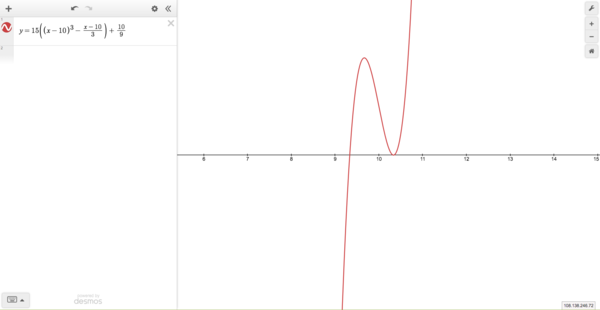
+*If <math>D<0</math>, then all three roots are real and distinct;
+[[Image:Cubic delta less 0.png|thumb|center|600x600px]]
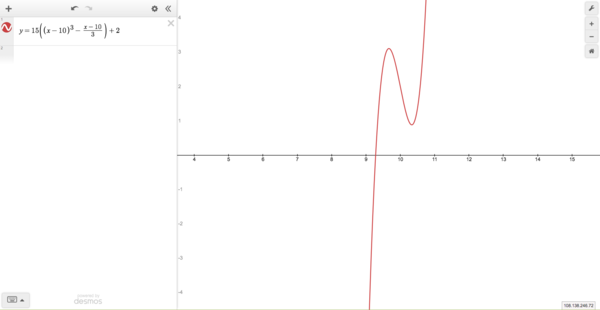
+*If <math>D>0</math>, then one of the roots is real and the other two are complex conjugate.
+[[Image:Cubic delta greater 0.png|thumb|center|600x600px]]
+====When <math>n=4</math>====
+The [[quartic Equation|quartic polynomial]] <math>p(x)=ax^4+bx^3+cx^2+dx+e</math> has discriminant
+<math>D(p)=256a^3e^3-192a^2bde^2-128a^2c^2e^2+144a^2cd^2e-27a^2d^4+144ab^2ce^2-6ab^2d^2e-80abc^2de+18abcd^3+16ac^4e-4ac^3d^2-27b^4e^2+18b^3cde-4b^3d^3-4b^2c^3e+b^2c^2d^2</math>
+*If <math>D=0</math>, then at least two of the roots are equal;
+*If <math>D>0</math>, then the roots are all real or all non-real;
+*If <math>D<0</math>, then there are two real roots and two complex conjugate roots.
+====Some properties====
+For <math>n\geq4</math> we can say that
+*The polynomial has a multiple root if, and only if, <math>D=0</math>;
+*If <math>D>0</math>, with <math>k</math> being a positive integer such that <math>k\geq\frac{n}{4}</math>, with <math>n</math> being the degree of the polynomial, then there are <math>2k</math> pairs of complex conjugate roots  and <math>n-4k</math> real roots;
+*If <math>D<0</math>, with <math>k</math> being a positive integer such that <math>k\geq\frac{n-2}{4}</math>, then there are <math>2k+1</math> pairs of complex conjugate roots and <math>n-4k+2</math> real roots.
+== Example Problems ==
+=== Introductory ===
+* (AMC 12 2005) There are two values of <math>a</math> for which the equation <math>4x^2+ax+8x+9=0</math> has only one solution for <math>x</math>. What is the sum of these values of <math>a</math>?
+Solution: Since we want the <math>a</math>'s where there is only one solution for <math>x</math>, the discriminant has to be <math>0</math>. <math>(a+8)^2-4(4)(9)=a^2+16a-80=0</math>. The sum of these values of <math>a</math> is <math>-16</math>.
+=== Intermediate ===
+* [[1977_Canadian_MO_Problems/Problem_1 | 1977 Canadian MO Problem 1]]
+== Other resources ==
+* [http://en.wikipedia.org/wiki/Discriminant Wikipedia entry]
+[[Category:Algebra]]
+[[Category:Quadratic equations]]
+[[Category:Definition]]

Page

Toolbox

Search