Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1995 AIME Problems"

m
(→‎Problem 7)
 
(8 intermediate revisions by 7 users not shown)
Line 1: Line 1:
 +
{{AIME Problems|year=1995}}
 +
 
== Problem 1 ==
 
== Problem 1 ==
−
Square <math>\displaystyle S_{1}</math> is <math>1\times 1.</math>  For <math>i\ge 1,</math> the lengths of the sides of square <math>\displaystyle S_{i+1}</math> are half the lengths of the sides of square <math>\displaystyle S_{i},</math> two adjacent sides of square <math>\displaystyle S_{i}</math> are perpendicular bisectors of two adjacent sides of square <math>\displaystyle S_{i+1},</math> and the other two sides of square <math>\displaystyle S_{i+1},</math> are the perpendicular bisectors of two adjacent sides of square <math>\displaystyle S_{i+2}.</math>  The total area enclosed by at least one of <math>\displaystyle S_{1}, S_{2}, S_{3}, S_{4}, S_{5}</math> can be written in the form <math>\displaystyle m/n,</math> where <math>\displaystyle m</math> and <math>\displaystyle n</math> are relatively prime positive integers.  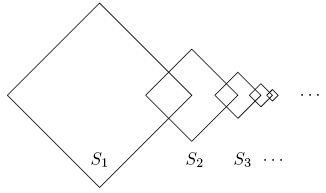Find <math>\displaystyle m-n.</math>
+
Square <math>S_{1}</math> is <math>1\times 1.</math>  For <math>i\ge 1,</math> the lengths of the sides of square <math>S_{i+1}</math> are half the lengths of the sides of square <math>S_{i},</math> two adjacent sides of square <math>S_{i}</math> are perpendicular bisectors of two adjacent sides of square <math>S_{i+1},</math> and the other two sides of square <math>S_{i+1},</math> are the perpendicular bisectors of two adjacent sides of square <math>S_{i+2}.</math>  The total area enclosed by at least one of <math>S_{1}, S_{2}, S_{3}, S_{4}, S_{5}</math> can be written in the form <math>m/n,</math> where <math>m</math> and <math>n</math> are relatively prime positive integers.  Find <math>m-n.</math>
  
 
[[Image:AIME 1995 Problem 1.png]]
 
[[Image:AIME 1995 Problem 1.png]]
Line 13: Line 15:
  
 
== Problem 3 ==
 
== Problem 3 ==
−
Starting at <math>\displaystyle (0,0),</math> an object moves in the coordinate plane via a sequence of steps, each of length one.  Each step is left, right, up, or down, all four equally likely.  Let <math>\displaystyle p</math> be the probability that the object reaches <math>\displaystyle (2,2)</math> in six or fewer steps.  Given that <math>\displaystyle p</math> can be written in the form <math>\displaystyle m/n,</math> where <math>\displaystyle m</math> and <math>\displaystyle n</math> are relatively prime positive integers, find <math>\displaystyle m+n.</math>
+
Starting at <math>(0,0),</math> an object moves in the coordinate plane via a sequence of steps, each of length one.  Each step is left, right, up, or down, all four equally likely.  Let <math>p</math> be the probability that the object reaches <math>(2,2)</math> in six or fewer steps.  Given that <math>p</math> can be written in the form <math>m/n,</math> where <math>m</math> and <math>n</math> are relatively prime positive integers, find <math>m+n.</math>
  
 
[[1995 AIME Problems/Problem 3|Solution]]
 
[[1995 AIME Problems/Problem 3|Solution]]
  
 
== Problem 4 ==
 
== Problem 4 ==
−
Circles of radius <math>\displaystyle 3</math> and <math>\displaystyle 6</math> are externally tangent to each other and are internally tangent to a circle of radius <math>\displaystyle 9</math>. The circle of radius <math>\displaystyle 9</math> has a chord that is a common external tangent of the other two circles. Find the square of the length of this chord.
+
Circles of radius <math>3</math> and <math>6</math> are externally tangent to each other and are internally tangent to a circle of radius <math>9</math>. The circle of radius <math>9</math> has a chord that is a common external tangent of the other two circles. Find the square of the length of this chord.
  
 
[[1995 AIME Problems/Problem 4|Solution]]
 
[[1995 AIME Problems/Problem 4|Solution]]
  
 
== Problem 5 ==
 
== Problem 5 ==
−
For certain real values of <math>\displaystyle a, b, c,</math> and <math>\displaystyle d_{},</math>  the equation <math>\displaystyle x^4+ax^3+bx^2+cx+d=0</math> has four non-real roots.  The product of two of these roots is <math>\displaystyle 13+i</math> and the sum of the other two roots is <math>\displaystyle 3+4i,</math> where <math>i=\sqrt{-1}.</math>  Find <math>\displaystyle b.</math>
+
For certain real values of <math>a, b, c,</math> and <math>d_{},</math>  the equation <math>x^4+ax^3+bx^2+cx+d=0</math> has four non-real roots.  The product of two of these roots is <math>13+i</math> and the sum of the other two roots is <math>3+4i,</math> where <math>i=\sqrt{-1}.</math>  Find <math>b.</math>
  
 
[[1995 AIME Problems/Problem 5|Solution]]
 
[[1995 AIME Problems/Problem 5|Solution]]
  
 
== Problem 6 ==
 
== Problem 6 ==
−
Let <math>\displaystyle n=2^{31}3^{19}.</math>  How many positive integer divisors of <math>\displaystyle n^2</math> are less than <math>\displaystyle n_{}</math> but do not divide <math>\displaystyle n_{}</math>?
+
Let <math>n=2^{31}3^{19}.</math>  How many positive integer divisors of <math>n^2</math> are less than <math>n_{}</math> but do not divide <math>n_{}</math>?
  
 
[[1995 AIME Problems/Problem 6|Solution]]
 
[[1995 AIME Problems/Problem 6|Solution]]
  
 
== Problem 7 ==
 
== Problem 7 ==
−
Given that <math>\displaystyle (1+\sin t)(1+\cos t)=5/4</math> and
+
Given that <math>(1+\sin t)(1+\cos t)=5/4</math> and
 
<center><math>(1-\sin t)(1-\cos t)=\frac mn-\sqrt{k},</math></center>
 
<center><math>(1-\sin t)(1-\cos t)=\frac mn-\sqrt{k},</math></center>
−
where <math>\displaystyle k, m,</math> and <math>\displaystyle n_{}</math> are positive integers with <math>\displaystyle m_{}</math> and <math>\displaystyle n_{}</math> relatively prime, find <math>\displaystyle k+m+n.</math>
+
where <math>k, m,</math> and <math>n_{}</math> are positive integers with <math>m_{}</math> and <math>n_{}</math> relatively prime, find <math>k+m+n.</math>
  
 
[[1995 AIME Problems/Problem 7|Solution]]
 
[[1995 AIME Problems/Problem 7|Solution]]
  
 
== Problem 8 ==
 
== Problem 8 ==
−
For how many ordered pairs of positive integers <math>\displaystyle (x,y),</math> with <math>\displaystyle y<x\le 100,</math> are both <math>\displaystyle \frac xy</math> and <math>\displaystyle \frac{x+1}{y+1}</math> integers?
+
For how many ordered pairs of positive integers <math>(x,y),</math> with <math>y<x\le 100,</math> are both <math>\frac xy</math> and <math>\frac{x+1}{y+1}</math> integers?
  
 
[[1995 AIME Problems/Problem 8|Solution]]
 
[[1995 AIME Problems/Problem 8|Solution]]
  
 
== Problem 9 ==
 
== Problem 9 ==
−
Triangle <math>\displaystyle ABC</math> is isosceles, with <math>\displaystyle AB=AC</math> and altitude <math>\displaystyle AM=11.</math>  Suppose that there is a point <math>\displaystyle D</math> on <math>\displaystyle \overline{AM}</math> with <math>\displaystyle AD=10</math> and <math>\displaystyle \angle BDC=3\angle BAC.</math>  Then the perimeter of <math>\displaystyle \triangle ABC</math> may be written in the form <math>\displaystyle a+\sqrt{b},</math> where <math>\displaystyle a</math> and <math>\displaystyle b</math> are integers.  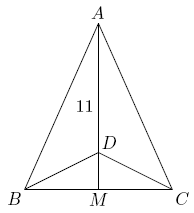Find <math>\displaystyle a+b.</math>
+
Triangle <math>ABC</math> is isosceles, with <math>AB=AC</math> and altitude <math>AM=11.</math>  Suppose that there is a point <math>D</math> on <math>\overline{AM}</math> with <math>AD=10</math> and <math>\angle BDC=3\angle BAC.</math>  Then the perimeter of <math>\triangle ABC</math> may be written in the form <math>a+\sqrt{b},</math> where <math>a</math> and <math>b</math> are integers.  Find <math>a+b.</math>
  
 
[[Image:AIME_1995_Problem_9.png]]
 
[[Image:AIME_1995_Problem_9.png]]
Line 57: Line 59:
  
 
== Problem 11 ==
 
== Problem 11 ==
−
A right rectangular prism <math>\displaystyle P_{}</math> (i.e., a rectangular parallelpiped) has sides of integral length <math>\displaystyle a, b, c,</math> with <math>\displaystyle a\le b\le c.</math>  A plane parallel to one of the faces of <math>\displaystyle P_{}</math> cuts <math>\displaystyle P_{}</math> into two prisms, one of which is similar to <math>\displaystyle P_{},</math> and both of which have nonzero volume.  Given that <math>\displaystyle b=1995,</math> for how many ordered triples <math>\displaystyle (a, b, c)</math> does such a plane exist?
+
A right rectangular prism <math>P_{}</math> (i.e., a rectangular parallelepiped) has sides of integral length <math>a, b, c,</math> with <math>a\le b\le c.</math>  A plane parallel to one of the faces of <math>P_{}</math> cuts <math>P_{}</math> into two prisms, one of which is similar to <math>P_{},</math> and both of which have nonzero volume.  Given that <math>b=1995,</math> for how many ordered triples <math>(a, b, c)</math> does such a plane exist?
  
 
[[1995 AIME Problems/Problem 11|Solution]]
 
[[1995 AIME Problems/Problem 11|Solution]]
  
 
== Problem 12 ==
 
== Problem 12 ==
−
Pyramid <math>\displaystyle OABCD</math> has square base <math>\displaystyle ABCD,</math> congruent edges <math>\displaystyle \overline{OA}, \overline{OB}, \overline{OC},</math> and <math>\displaystyle \overline{OD},</math> and <math>\displaystyle \angle AOB=45^\circ.</math>  Let <math>\displaystyle \theta</math> be the measure of the dihedral angle formed by faces <math>\displaystyle OAB</math> and <math>\displaystyle OBC.</math>  Given that <math>\displaystyle \cos \theta=m+\sqrt{n},</math> where <math>\displaystyle m_{}</math> and <math>\displaystyle n_{}</math> are integers, find <math>\displaystyle m+n.</math>
+
Pyramid <math>OABCD</math> has square base <math>ABCD,</math> congruent edges <math>\overline{OA}, \overline{OB}, \overline{OC},</math> and <math>\overline{OD},</math> and <math>\angle AOB=45^\circ.</math>  Let <math>\theta</math> be the measure of the dihedral angle formed by faces <math>OAB</math> and <math>OBC.</math>  Given that <math>\cos \theta=m+\sqrt{n},</math> where <math>m_{}</math> and <math>n_{}</math> are integers, find <math>m+n.</math>
  
 
[[1995 AIME Problems/Problem 12|Solution]]
 
[[1995 AIME Problems/Problem 12|Solution]]
  
 
== Problem 13 ==
 
== Problem 13 ==
−
Let <math>\displaystyle f(n)</math> be the integer closest to <math>\displaystyle \sqrt[4]{n}.</math>  Find <math>\displaystyle \sum_{k=1}^{1995}\frac 1{f(k)}.</math>
+
Let <math>f(n)</math> be the integer closest to <math>\sqrt[4]{n}.</math>  Find <math>\sum_{k=1}^{1995}\frac 1{f(k)}.</math>
  
 
[[1995 AIME Problems/Problem 13|Solution]]
 
[[1995 AIME Problems/Problem 13|Solution]]
  
 
== Problem 14 ==
 
== Problem 14 ==
 +
In a circle of radius 42, two chords of length 78 intersect at a point whose distance from the center is 18.  The two chords divide the interior of the circle into four regions.  Two of these regions are bordered by segments of unequal lengths, and the area of either of them can be expressed uniquely in the form <math>m\pi-n\sqrt{d},</math> where <math>m, n,</math> and <math>d_{}</math> are positive integers and <math>d_{}</math> is not divisible by the square of any prime number.  Find <math>m+n+d.</math>
  
 
[[1995 AIME Problems/Problem 14|Solution]]
 
[[1995 AIME Problems/Problem 14|Solution]]
  
 
== Problem 15 ==
 
== Problem 15 ==
 +
Let <math>p_{}</math> be the probability that, in the process of repeatedly flipping a fair coin, one will encounter a run of 5 heads before one encounters a run of 2 tails.  Given that <math>p_{}</math> can be written in the form <math>m/n</math> where <math>m_{}</math> and <math>n_{}</math> are relatively prime positive integers, find <math>m+n</math>.
  
 
[[1995 AIME Problems/Problem 15|Solution]]
 
[[1995 AIME Problems/Problem 15|Solution]]
  
 
== See also ==
 
== See also ==
 +
 +
{{AIME box|year=1995|before=[[1994 AIME Problems]]|after=[[1996 AIME Problems]]}}
 +
 
* [[American Invitational Mathematics Examination]]
 
* [[American Invitational Mathematics Examination]]
 
* [[AIME Problems and Solutions]]
 
* [[AIME Problems and Solutions]]
 
* [[Mathematics competition resources]]
 
* [[Mathematics competition resources]]
 +
{{MAA Notice}}

Latest revision as of 23:25, 26 March 2024

1995 AIME (Answer Key)
Printable version | AoPS Contest Collections • PDF

Instructions

  1. This is a 15-question, 3-hour examination. All answers are integers ranging from $000$ to $999$, inclusive. Your score will be the number of correct answers; i.e., there is neither partial credit nor a penalty for wrong answers.
  2. No aids other than scratch paper, graph paper, ruler, compass, and protractor are permitted. In particular, calculators and computers are not permitted.
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15

Problem 1

Square $S_{1}$ is $1\times 1.$ For $i\ge 1,$ the lengths of the sides of square $S_{i+1}$ are half the lengths of the sides of square $S_{i},$ two adjacent sides of square $S_{i}$ are perpendicular bisectors of two adjacent sides of square $S_{i+1},$ and the other two sides of square $S_{i+1},$ are the perpendicular bisectors of two adjacent sides of square $S_{i+2}.$ The total area enclosed by at least one of $S_{1}, S_{2}, S_{3}, S_{4}, S_{5}$ can be written in the form $m/n,$ where $m$ and $n$ are relatively prime positive integers. Find $m-n.$

AIME 1995 Problem 1.png

Solution

Problem 2

Find the last three digits of the product of the positive roots of $\sqrt{1995}x^{\log_{1995}x}=x^2.$

Solution

Problem 3

Starting at $(0,0),$ an object moves in the coordinate plane via a sequence of steps, each of length one. Each step is left, right, up, or down, all four equally likely. Let $p$ be the probability that the object reaches $(2,2)$ in six or fewer steps. Given that $p$ can be written in the form $m/n,$ where $m$ and $n$ are relatively prime positive integers, find $m+n.$

Solution

Problem 4

Circles of radius $3$ and $6$ are externally tangent to each other and are internally tangent to a circle of radius $9$. The circle of radius $9$ has a chord that is a common external tangent of the other two circles. Find the square of the length of this chord.

Solution

Problem 5

For certain real values of $a, b, c,$ and $d_{},$ the equation $x^4+ax^3+bx^2+cx+d=0$ has four non-real roots. The product of two of these roots is $13+i$ and the sum of the other two roots is $3+4i,$ where $i=\sqrt{-1}.$ Find $b.$

Solution

Problem 6

Let $n=2^{31}3^{19}.$ How many positive integer divisors of $n^2$ are less than $n_{}$ but do not divide $n_{}$?

Solution

Problem 7

Given that $(1+\sin t)(1+\cos t)=5/4$ and

$(1-\sin t)(1-\cos t)=\frac mn-\sqrt{k},$

where $k, m,$ and $n_{}$ are positive integers with $m_{}$ and $n_{}$ relatively prime, find $k+m+n.$

Solution

Problem 8

For how many ordered pairs of positive integers $(x,y),$ with $y<x\le 100,$ are both $\frac xy$ and $\frac{x+1}{y+1}$ integers?

Solution

Problem 9

Triangle $ABC$ is isosceles, with $AB=AC$ and altitude $AM=11.$ Suppose that there is a point $D$ on $\overline{AM}$ with $AD=10$ and $\angle BDC=3\angle BAC.$ Then the perimeter of $\triangle ABC$ may be written in the form $a+\sqrt{b},$ where $a$ and $b$ are integers. Find $a+b.$

AIME 1995 Problem 9.png

Solution

Problem 10

What is the largest positive integer that is not the sum of a positive integral multiple of 42 and a positive composite integer?

Solution

Problem 11

A right rectangular prism $P_{}$ (i.e., a rectangular parallelepiped) has sides of integral length $a, b, c,$ with $a\le b\le c.$ A plane parallel to one of the faces of $P_{}$ cuts $P_{}$ into two prisms, one of which is similar to $P_{},$ and both of which have nonzero volume. Given that $b=1995,$ for how many ordered triples $(a, b, c)$ does such a plane exist?

Solution

Problem 12

Pyramid $OABCD$ has square base $ABCD,$ congruent edges $\overline{OA}, \overline{OB}, \overline{OC},$ and $\overline{OD},$ and $\angle AOB=45^\circ.$ Let $\theta$ be the measure of the dihedral angle formed by faces $OAB$ and $OBC.$ Given that $\cos \theta=m+\sqrt{n},$ where $m_{}$ and $n_{}$ are integers, find $m+n.$

Solution

Problem 13

Let $f(n)$ be the integer closest to $\sqrt[4]{n}.$ Find $\sum_{k=1}^{1995}\frac 1{f(k)}.$

Solution

Problem 14

In a circle of radius 42, two chords of length 78 intersect at a point whose distance from the center is 18. The two chords divide the interior of the circle into four regions. Two of these regions are bordered by segments of unequal lengths, and the area of either of them can be expressed uniquely in the form $m\pi-n\sqrt{d},$ where $m, n,$ and $d_{}$ are positive integers and $d_{}$ is not divisible by the square of any prime number. Find $m+n+d.$

Solution

Problem 15

Let $p_{}$ be the probability that, in the process of repeatedly flipping a fair coin, one will encounter a run of 5 heads before one encounters a run of 2 tails. Given that $p_{}$ can be written in the form $m/n$ where $m_{}$ and $n_{}$ are relatively prime positive integers, find $m+n$.

Solution

See also

1995 AIME (Problems • Answer Key • Resources)
Preceded by
1994 AIME Problems 		Followed by
1996 AIME Problems
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1995_AIME_Problems&oldid=217476"