Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2023 AIME II Problems/Problem 14"

m (→‎Solution (3-d vector analysis, analytic geometry + Calculus))
 
(13 intermediate revisions by 7 users not shown)
Line 1: Line 1:
 
==Problem==
 
==Problem==
−
A cube-shaped container has vertices <math>A,</math> <math>B,</math> <math>C,</math> and <math>D,</math> where <math>\overline{AB}</math> and <math>\overline{CD}</math> are parallel edges of the cube, and <math>\overline{AC}</math> and <math>\overline{BD}</math> are diagonals of faces of the cube, as shown. Vertex <math>A</math> of the cube is set on a horizontal plane <math>\mathcal{P}</math> so that the plane of the rectangle <math>ABDC</math> is perpendicular to <math>\mathcal{P},</math> vertex <math>B</math> is <math>2</math> meters above <math>\mathcal{P},</math> vertex <math>C</math> is <math>8</math> meters above <math>\mathcal{P},</math> and vertex <math>D</math> is <math>10</math> meters above <math>\mathcal{P}.</math> The cube contains water whose surface is parallel to <math>\mathcal{P}</math> at a height of <math>7</math> meters above <math>\mathcal{P}.</math> The volume of water is <math>\frac{m}{n}</math> cubic meters, where <math>m</math> and <math>n</math> are relatively prime positive intgers. Find <math>m+n.</math>
+
A cube-shaped container has vertices <math>A,</math> <math>B,</math> <math>C,</math> and <math>D,</math> where <math>\overline{AB}</math> and <math>\overline{CD}</math> are parallel edges of the cube, and <math>\overline{AC}</math> and <math>\overline{BD}</math> are diagonals of faces of the cube, as shown. Vertex <math>A</math> of the cube is set on a horizontal plane <math>\mathcal{P}</math> so that the plane of the rectangle <math>ABDC</math> is perpendicular to <math>\mathcal{P},</math> vertex <math>B</math> is <math>2</math> meters above <math>\mathcal{P},</math> vertex <math>C</math> is <math>8</math> meters above <math>\mathcal{P},</math> and vertex <math>D</math> is <math>10</math> meters above <math>\mathcal{P}.</math> The cube contains water whose surface is parallel to <math>\mathcal{P}</math> at a height of <math>7</math> meters above <math>\mathcal{P}.</math> The volume of water is <math>\frac{m}{n}</math> cubic meters, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n.</math>
  
 +
==Diagram==
 +
<asy>
 +
//Made by Djmathman
 +
size(250);
 +
defaultpen(linewidth(0.6));
 +
pair A = origin, B = (6,3), X = rotate(40)*B, Y = rotate(70)*X, C = X+Y, Z = X+B, D = B+C, W = B+Y;
 +
pair P1 = 0.8*C+0.2*Y, P2 = 2/3*C+1/3*X, P3 = 0.2*D+0.8*Z, P4 = 0.63*D+0.37*W;
 +
pair E = (-20,6), F = (-6,-5), G = (18,-2), H = (9,8);
 +
filldraw(E--F--G--H--cycle,rgb(0.98,0.98,0.2));
 +
fill(A--Y--P1--P4--P3--Z--B--cycle,rgb(0.35,0.7,0.9));
 +
draw(A--B--Z--X--A--Y--C--X^^C--D--Z);
 +
draw(P1--P2--P3--P4--cycle^^D--P4);
 +
dot("$A$",A,S);
 +
dot("$B$",B,S);
 +
dot("$C$",C,N);
 +
dot("$D$",D,N);
 +
label("$\mathcal P$",(-13,4.5));
 +
</asy>
  
−
==Solution (3-d vector analysis, analytic geometry + Calculus)==
+
==Solution 1==
 +
 
 +
<asy>
 +
defaultpen(linewidth(0.6));
 +
pair A = (0, 0), B = (5.656,2), C = (-2.828, 8), D = B+C, P = 0.875*C, Q = B+0.625*C, H = (-2.828, 0), G = (5.656, 0);
 +
pair P1 = (-5, 0), P2 = (10, 0);
 +
draw(A--B--D--C--A);
 +
filldraw(A--B--Q--P--cycle,rgb(0.35,0.7,0.9));
 +
draw(C--H, dotted);
 +
draw(B--G, dotted);
 +
draw(P1--P2);
 +
dot("$A$",A,S);
 +
dot("$B$",B,E);
 +
dot("$C$",C,N);
 +
dot("$D$",D,N);
 +
dot("$H$",H,S);
 +
dot("$G$",G,S);
 +
dot("$P$",P,SE);
 +
dot("$Q$",Q,E);
 +
label("$\mathcal P$",(11, 0));
 +
</asy>
 +
 
 +
Let's first view the cube from a direction perpendicular to <math>ABDC</math>, as illustrated above. Let <math>x</math> be the cube's side length. Since <math>\triangle CHA \sim \triangle AGB</math>, we have
 +
<cmath>\frac{CA}{CH} = \frac{AB}{AG}.</cmath>
 +
We know <math>AB = x</math>, <math>AG = \sqrt{x^2-2^2}</math>, <math>AC = \sqrt{2}x</math>, <math>CH = 8</math>. Plug them into the above equation, we get
 +
<cmath>\frac{\sqrt{2}x}{8} = \frac{x}{\sqrt{x^2-2^2}}.</cmath>
 +
Solving this we get the cube's side length <math>x = 6</math>, and <math>AC = 6\sqrt{2}.</math>
 +
 
 +
Let <math>PQ</math> be the water's surface, both <math>P</math> and <math>Q</math> are <math>7</math> meters from <math>\mathcal P</math>. Notice that <math>C</math> is <math>8</math> meters from <math>\mathcal P</math>, this means
 +
<cmath>CP = \frac{1}{8}CA = \frac{3\sqrt{2}}{4}.</cmath>
 +
Similarly,
 +
<cmath>DQ = \frac{3}{8}CA = \frac{9\sqrt{2}}{4}.</cmath>
 +
 
 +
<asy>
 +
defaultpen(linewidth(0.6));
 +
pair A = (0, 0), C = (0, 2*6), X = (6, 6), Y = (-6, 6), P = (0, 1.75*6), I = (-0.25*6, 1.75*6), J = (0.25*6, 1.75*6);
 +
pair P1 = (-8, 0), P2 = (8, 0);
 +
draw(A--X--C--Y--A);
 +
filldraw(A--X--J--I--Y--cycle,rgb(0.35,0.7,0.9));
 +
draw(P1--P2, dotted);
 +
dot("$A$",A,S);
 +
dot("$C$",C,N);
 +
dot("$P$",P,S);
 +
label("$\mathcal P$",(10, 0));
 +
</asy>
 +
 
 +
Now, we realize that the 3D space inside the cube without water is a frustum, with <math>P</math> on its smaller base and <math>Q</math> on its larger base. To find its volume, all we need is to find the areas of both bases and the height, which is <math>x = 6</math>. To find the smaller base, let's move our viewpoint onto the plane <math>ABDC</math> and view the cube from a direction parallel to <math>ABDC</math>, as shown above. The area of the smaller base is simply
 +
<cmath> S_1 = CP^2 = \Bigl(\frac{3\sqrt{2}}{4}\Bigr)^2 = \frac{9}{8}.</cmath>
 +
Similarly, the area of the larger base is
 +
<cmath> S_2 = DQ^2 = \Bigl(\frac{9\sqrt{2}}{4}\Bigr)^2 = \frac{81}{8}.</cmath>
 +
 
 +
Finally, applying the formula for a frustum's volume,
 +
 
 +
<cmath> V = \frac{1}{3} \cdot x \cdot (S_1 + \sqrt{S_1S_2} + S_2) = \frac{1}{3} \cdot 6 \cdot \Bigl(\frac{9}{8} + \sqrt{\frac{9}{8}\cdot\frac{81}{8}} + \frac{81}{8}\Bigl) = \frac{117}{4}.</cmath>
 +
 
 +
The water's volume is thus
 +
<cmath> 6^3 - \frac{117}{4} = \frac{747}{4},</cmath>
 +
giving <math>\boxed{751}</math>.
 +
 
 +
==Solution 2==
 +
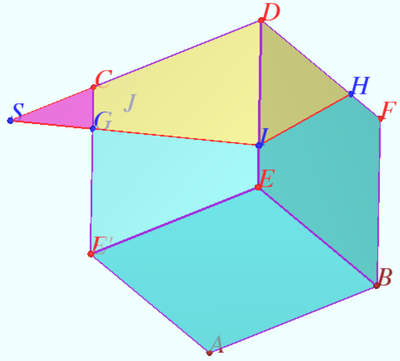
[[File:2023 AIME II 14.png|400px|right]]
 +
Denote <math>h(X)</math> the distance from point <math>X</math> to <math>\mathcal{P},  h(A) = 0, h(B) = 2,</math>
 +
<math>h(C) = 8, h(D) = 10, h(G) = h(I) = h(H) = 7,  AB = a, AC = a \sqrt{2}.</math>
 +
 
 +
Let slope <math>AB</math> to <math>\mathcal{P}</math> be <math>\alpha.</math> Notation is shown in the diagram.
 +
<cmath>\tan \alpha = \frac {\sin \alpha}{\cos \alpha} = \frac {h(B)}{AB}\cdot \frac {AC}{h(C)} = \frac {\sqrt{2}}{4} \implies a = 6.</cmath>
 +
Let <math>S = GI \cap CD \implies h(S) = h(G) = 7.</math>
 +
<cmath>h(C) – h(G) = 8 - 7 = 1, h(D)- h(I) = 10 - 7 = 3.</cmath>
 +
<cmath>h(E) = h(F) = \frac {h(D) +h(B)}{2} = 6 \implies</cmath>
 +
<cmath>\frac {DI}{DE} = \frac {h(D) - h(I)}{h(D)-h(E)} = \frac {3}{4} \implies DI = DH = \frac {9}{2}.</cmath>
 +
 
 +
Similarly <math>CG = \frac {3}{2} \implies SD = 9.</math>
 +
 
 +
Let the volume without water be <math>V,</math> volume of the pyramid <math>SCGJ</math> be <math>U.</math>
 +
 
 +
It is clear that <math>U + V = 27U = \frac {SD}{6} \cdot DI^2 = \frac {243}{8} \implies</math>
 +
<math>V = \frac {243 \cdot 26}{8 \cdot 27 } = \frac {117}{4} = 6^3 - \frac {747}{4}</math>  from which <math>\boxed{751}.</math>
 +
 
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 
 +
==Solution 3==
  
 
We introduce a Cartesian coordinate system to the diagram.
 
We introduce a Cartesian coordinate system to the diagram.
Line 75: Line 173:
  
 
By solving these equations, we get
 
By solving these equations, we get
−
\[
+
<math>y_P^2 + y_Q^2 = 36 .</math>
−
y_P^2 + y_Q^2 = 36 .
+
 
−
]\
 
  
 
In addition, we have <math>\overrightarrow{AC} = \overrightarrow{AP} + \overrightarrow{AQ}</math>.
 
In addition, we have <math>\overrightarrow{AC} = \overrightarrow{AP} + \overrightarrow{AQ}</math>.
Line 125: Line 222:
  
 
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
 
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
 +
 +
== Video Solution ==
 +
https://youtu.be/6YCtKO7UW3s
  
 
== See also ==
 
== See also ==

Latest revision as of 15:42, 8 March 2024

Problem

A cube-shaped container has vertices $A,$ $B,$ $C,$ and $D,$ where $\overline{AB}$ and $\overline{CD}$ are parallel edges of the cube, and $\overline{AC}$ and $\overline{BD}$ are diagonals of faces of the cube, as shown. Vertex $A$ of the cube is set on a horizontal plane $\mathcal{P}$ so that the plane of the rectangle $ABDC$ is perpendicular to $\mathcal{P},$ vertex $B$ is $2$ meters above $\mathcal{P},$ vertex $C$ is $8$ meters above $\mathcal{P},$ and vertex $D$ is $10$ meters above $\mathcal{P}.$ The cube contains water whose surface is parallel to $\mathcal{P}$ at a height of $7$ meters above $\mathcal{P}.$ The volume of water is $\frac{m}{n}$ cubic meters, where $m$ and $n$ are relatively prime positive integers. Find $m+n.$

Diagram

[asy] //Made by Djmathman size(250); defaultpen(linewidth(0.6)); pair A = origin, B = (6,3), X = rotate(40)*B, Y = rotate(70)*X, C = X+Y, Z = X+B, D = B+C, W = B+Y; pair P1 = 0.8*C+0.2*Y, P2 = 2/3*C+1/3*X, P3 = 0.2*D+0.8*Z, P4 = 0.63*D+0.37*W; pair E = (-20,6), F = (-6,-5), G = (18,-2), H = (9,8); filldraw(E--F--G--H--cycle,rgb(0.98,0.98,0.2)); fill(A--Y--P1--P4--P3--Z--B--cycle,rgb(0.35,0.7,0.9)); draw(A--B--Z--X--A--Y--C--X^^C--D--Z); draw(P1--P2--P3--P4--cycle^^D--P4); dot("$A$",A,S); dot("$B$",B,S); dot("$C$",C,N); dot("$D$",D,N); label("$\mathcal P$",(-13,4.5)); [/asy]

Solution 1

[asy] defaultpen(linewidth(0.6)); pair A = (0, 0), B = (5.656,2), C = (-2.828, 8), D = B+C, P = 0.875*C, Q = B+0.625*C, H = (-2.828, 0), G = (5.656, 0); pair P1 = (-5, 0), P2 = (10, 0); draw(A--B--D--C--A); filldraw(A--B--Q--P--cycle,rgb(0.35,0.7,0.9)); draw(C--H, dotted); draw(B--G, dotted); draw(P1--P2); dot("$A$",A,S); dot("$B$",B,E); dot("$C$",C,N); dot("$D$",D,N); dot("$H$",H,S); dot("$G$",G,S); dot("$P$",P,SE); dot("$Q$",Q,E); label("$\mathcal P$",(11, 0)); [/asy]

Let's first view the cube from a direction perpendicular to $ABDC$, as illustrated above. Let $x$ be the cube's side length. Since $\triangle CHA \sim \triangle AGB$, we have \[\frac{CA}{CH} = \frac{AB}{AG}.\] We know $AB = x$, $AG = \sqrt{x^2-2^2}$, $AC = \sqrt{2}x$, $CH = 8$. Plug them into the above equation, we get \[\frac{\sqrt{2}x}{8} = \frac{x}{\sqrt{x^2-2^2}}.\] Solving this we get the cube's side length $x = 6$, and $AC = 6\sqrt{2}.$

Let $PQ$ be the water's surface, both $P$ and $Q$ are $7$ meters from $\mathcal P$. Notice that $C$ is $8$ meters from $\mathcal P$, this means \[CP = \frac{1}{8}CA = \frac{3\sqrt{2}}{4}.\] Similarly, \[DQ = \frac{3}{8}CA = \frac{9\sqrt{2}}{4}.\]

[asy] defaultpen(linewidth(0.6)); pair A = (0, 0), C = (0, 2*6), X = (6, 6), Y = (-6, 6), P = (0, 1.75*6), I = (-0.25*6, 1.75*6), J = (0.25*6, 1.75*6); pair P1 = (-8, 0), P2 = (8, 0); draw(A--X--C--Y--A); filldraw(A--X--J--I--Y--cycle,rgb(0.35,0.7,0.9)); draw(P1--P2, dotted); dot("$A$",A,S); dot("$C$",C,N); dot("$P$",P,S); label("$\mathcal P$",(10, 0)); [/asy]

Now, we realize that the 3D space inside the cube without water is a frustum, with $P$ on its smaller base and $Q$ on its larger base. To find its volume, all we need is to find the areas of both bases and the height, which is $x = 6$. To find the smaller base, let's move our viewpoint onto the plane $ABDC$ and view the cube from a direction parallel to $ABDC$, as shown above. The area of the smaller base is simply \[S_1 = CP^2 = \Bigl(\frac{3\sqrt{2}}{4}\Bigr)^2 = \frac{9}{8}.\] Similarly, the area of the larger base is \[S_2 = DQ^2 = \Bigl(\frac{9\sqrt{2}}{4}\Bigr)^2 = \frac{81}{8}.\]

Finally, applying the formula for a frustum's volume,

\[V = \frac{1}{3} \cdot x \cdot (S_1 + \sqrt{S_1S_2} + S_2) = \frac{1}{3} \cdot 6 \cdot \Bigl(\frac{9}{8} + \sqrt{\frac{9}{8}\cdot\frac{81}{8}} + \frac{81}{8}\Bigl) = \frac{117}{4}.\]

The water's volume is thus \[6^3 - \frac{117}{4} = \frac{747}{4},\] giving $\boxed{751}$.

Solution 2

2023 AIME II 14.png

Denote $h(X)$ the distance from point $X$ to $\mathcal{P}, h(A) = 0, h(B) = 2,$ $h(C) = 8, h(D) = 10, h(G) = h(I) = h(H) = 7, AB = a, AC = a \sqrt{2}.$

Let slope $AB$ to $\mathcal{P}$ be $\alpha.$ Notation is shown in the diagram. \[\tan \alpha = \frac {\sin \alpha}{\cos \alpha} = \frac {h(B)}{AB}\cdot \frac {AC}{h(C)} = \frac {\sqrt{2}}{4} \implies a = 6.\] Let $S = GI \cap CD \implies h(S) = h(G) = 7.$ \[h(C) – h(G) = 8 - 7 = 1, h(D)- h(I) = 10 - 7 = 3.\] \[h(E) = h(F) = \frac {h(D) +h(B)}{2} = 6 \implies\] \[\frac {DI}{DE} = \frac {h(D) - h(I)}{h(D)-h(E)} = \frac {3}{4} \implies DI = DH = \frac {9}{2}.\]

Similarly $CG = \frac {3}{2} \implies SD = 9.$

Let the volume without water be $V,$ volume of the pyramid $SCGJ$ be $U.$

It is clear that $U + V = 27U = \frac {SD}{6} \cdot DI^2 = \frac {243}{8} \implies$ $V = \frac {243 \cdot 26}{8 \cdot 27 } = \frac {117}{4} = 6^3 - \frac {747}{4}$ from which $\boxed{751}.$

vladimir.shelomovskii@gmail.com, vvsss

Solution 3

We introduce a Cartesian coordinate system to the diagram. We put the origin at $A$. We let the $z$-components of $B$, $C$, $D$ be positive. We set the $x$-axis in a direction such that $B$ is on the $x-O-z$ plane.

The coordinates of $A$, $B$, $C$ are $A = \left( 0, 0, 0 \right)$, $B = \left( x_B, 0 , 2 \right)$, $C = \left( x_C, y_C, 8 \right)$.

Because $AB \perp AC$, $\overrightarrow{AB} \cdot \overrightarrow{AC} = 0$. Thus, \[ x_B x_C + 16 = 0 . \hspace{1cm} (1) \]

Because $AC$ is a diagonal of a face, $AC^2 = 2 AB^2$. Thus, \[ x_C^2 + y_C^2 + 8^2 = 2 \left( x_B^2 + 2^2 \right) . \hspace{1cm} (2) \]

Because plane $ABCD$ is perpendicular to plan $P$, $\hat z \cdot \left( \overrightarrow{AB} \times \overrightarrow{AC} \right) = 0$. Thus, \[ \begin{vmatrix} 0 & 0 & 1 \\ x_B & 0 & 2 \\ x_C & y_C & 8 \end{vmatrix} = 0 . \hspace{1cm} (3) \]

Jointly solving (1), (2), (3), we get one solution $x_B = 4 \sqrt{2}$, $x_C = - 2 \sqrt{2}$, $y_C = 0$. Thus, the side length of the cube is $|AB| = \sqrt{x_B^2 + 2^2} = 6$.

Denote by $P$ and $Q$ two vertices such that $AP$ and $AQ$ are two edges, and satisfy the right-hand rule that $\widehat{AB} \times \widehat{AP} = \widehat{AQ}$. Now, we compute the coordinates of $P$ and $Q$.

Because $|AB| = 6$, we have $\overrightarrow{AP} \times \overrightarrow{AQ} = 6 \overrightarrow{AB}$, $\overrightarrow{AQ} \times \overrightarrow{AB} = 6 \overrightarrow{AP}$, $\overrightarrow{AB} \times \overrightarrow{AP} = 6 \overrightarrow{AQ}$.

Hence, \begin{align*} \begin{bmatrix} \hat i & \hat j & \hat k \\ x_P & y_P & z_P \\ x_Q & y_Q & z_Q \end{bmatrix} & = 6 \left( 4 \sqrt{2} \hat i + 2 \hat k \right) , \\ \begin{vmatrix} \hat i & \hat j & \hat k \\ x_Q & y_Q & z_Q \\ 4 \sqrt{2} & 0 & 2 \end{vmatrix} & = 6 \left( x_P \hat i + y_P \hat j + z_P \hat k \right) , \\ \begin{vmatrix} \hat i & \hat j & \hat k \\ 4 \sqrt{2} & 0 & 2 \\ x_P & y_P & z_P \end{vmatrix} & = 6 \left( x_Q \hat i + y_Q \hat j + z_Q \hat k \right) . \end{align*}

By solving these equations, we get $y_P^2 + y_Q^2 = 36 .$


In addition, we have $\overrightarrow{AC} = \overrightarrow{AP} + \overrightarrow{AQ}$. Thus, $P = \left( - \sqrt{2} , 3 \sqrt{2} , 4 \right)$, $Q = \left( - \sqrt{2} , - 3 \sqrt{2} , 4 \right)$.

Therefore, the volume of the water is \begin{align*} V = & 6^3 \int_{u=0}^1 \int_{v=0}^1 \int_{w=0}^1 \mathbf 1 \left\{ z_B u + z_P v + z_Q w \leq 7 \right\} dw dv du \\ & = 6^3 \int_{u=0}^1 \int_{v=0}^1 \int_{w=0}^1 \mathbf 1 \left\{ 2 u + 4 v + 4 w \leq 7 \right\} dw dv du \\ & = 6^3 - 6^3 \int_{u=0}^1 \int_{v=0}^1 \int_{w=0}^1 \mathbf 1 \left\{ 2 u + 4 v + 4 w > 7 \right\} dw dv du . \end{align*}

Define $u' = 1 - u$, $v' = 1 - v$, $w' = 1 - w$. Thus, \begin{align*} V & = 6^3 - 6^3 \int_{u=0}^1 \int_{v=0}^1 \int_{w=0}^1 \mathbf 1 \left\{ 2 u' + 4 v' + 4 w' < 3 \right\} dw dv du \\ & = 6^3 - 6^3 \int_{u'=0}^1 \left( \int_{v'=0}^1 \int_{w'=0}^1 \mathbf 1 \left\{ v' + w' < \frac{3}{4} - \frac{u'}{2} \right\} dw' dv' \right) du' \\ & = 6^3 - 6^3 \int_{u'=0}^1 \frac{1}{2} \left( \frac{3}{4} - \frac{u'}{2} \right)^2 du' . \end{align*}

Define $u'' = \frac{3}{4} - \frac{u'}{2}$. Thus, \begin{align*} V & = 6^3 - 6^3 \int_{u'' = 1/4}^{3/4} \left( u'' \right)^2 du'' \\ & = 6^3 - 6^3 \frac{1}{3} \left( \left(\frac{3}{4}\right)^3 - \left(\frac{1}{4}\right)^3 \right) \\ & = 216 - \frac{117}{4} \\ & = \frac{747}{4} . \end{align*}

Therefore, the answer is $747 + 4 = \boxed{\textbf{(751) }}$.

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Video Solution

https://youtu.be/6YCtKO7UW3s

See also

2023 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 13 		Followed by
Problem 15
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2023_AIME_II_Problems/Problem_14&oldid=216616"