Difference between revisions of "2021 AIME I Problems/Problem 13"
m (→Solution) |
(→Solution 1 (Radical Axis)) |
||
| (47 intermediate revisions by 12 users not shown) | |||
| Line 2: | Line 2: | ||
Circles <math>\omega_1</math> and <math>\omega_2</math> with radii <math>961</math> and <math>625</math>, respectively, intersect at distinct points <math>A</math> and <math>B</math>. A third circle <math>\omega</math> is externally tangent to both <math>\omega_1</math> and <math>\omega_2</math>. Suppose line <math>AB</math> intersects <math>\omega</math> at two points <math>P</math> and <math>Q</math> such that the measure of minor arc <math>\widehat{PQ}</math> is <math>120^{\circ}</math>. Find the distance between the centers of <math>\omega_1</math> and <math>\omega_2</math>. | Circles <math>\omega_1</math> and <math>\omega_2</math> with radii <math>961</math> and <math>625</math>, respectively, intersect at distinct points <math>A</math> and <math>B</math>. A third circle <math>\omega</math> is externally tangent to both <math>\omega_1</math> and <math>\omega_2</math>. Suppose line <math>AB</math> intersects <math>\omega</math> at two points <math>P</math> and <math>Q</math> such that the measure of minor arc <math>\widehat{PQ}</math> is <math>120^{\circ}</math>. Find the distance between the centers of <math>\omega_1</math> and <math>\omega_2</math>. | ||
| − | ==Solution== | + | ==Quick, Olympiad-Style Solution== |
| + | |||
| + | Let <math>D\equiv\omega\cap\omega_{1}</math> and <math>E\equiv\omega\cap\omega_{2}</math>. The solution relies on the following key claim: | ||
| + | |||
| + | <font color=red><b>Claim.</b></font color> <math>DPEQ</math> is a harmonic quadrilateral. | ||
| + | |||
| + | <font color=blue><b>Proof.</b></font color> Using the radical axis theorem, the tangents to circle <math>\omega</math> at <math>D</math> and <math>E</math> are concurrent with line <math>\overline{ABPQ}</math> at the radical center, implying that our claim is true by harmonic quadrilateral properties. <math>\blacksquare</math> | ||
| + | |||
| + | Thus, we deduce the tangents to <math>\omega</math> at <math>P</math> and <math>Q</math> are concurrent at <math>F</math> with line <math>\overline{DE}</math>. Denote by <math>O_{1}, O_{2}, O</math> the centers of <math>\omega_{1}, \omega_{2}, \omega</math> respectively. | ||
| + | |||
| + | Now suppose <math>G\equiv\overline{FDE}\cap\overline{O_{1}O_{2}}</math>. Note that <math>\overline{OF}\parallel\overline{O_{1}O_{2}}</math> giving us the pairs of similar triangles <cmath>\triangle O_{1}GD\sim\triangle OFD~\text{and}~\triangle O_{2}GE\sim\triangle OFE.</cmath> We thereby obtain <cmath>\dfrac{O_{1}G}{O_{1}D}=\dfrac{OF}{OD}=\dfrac{r\sec\tfrac{120^{\circ}}{2}}{r}=\sec 60^{\circ}=2</cmath> since <math>\widehat{PQ}=120^{\circ}</math>, where <math>r</math> denotes the radius of <math>\omega</math>, and <cmath>\dfrac{O_{2}G}{O_{2}E}=\dfrac{OF}{OE}=\sec 60^{\circ}=2</cmath> as well. It follows that <cmath>O_{1}O_{2}=O_{1}G-O_{2}G=2(O_{1}D-O_{2}E)=2(961-625)=\textbf{672}.</cmath> | ||
| + | |||
| + | [[File:AIME 2021-I13 Geogebra Diagram.png|672px]] | ||
| + | |||
| + | ==Solution 1 (Radical Axis)== | ||
Let <math>O_i</math> and <math>r_i</math> be the center and radius of <math>\omega_i</math>, and let <math>O</math> and <math>r</math> be the center and radius of <math>\omega</math>. | Let <math>O_i</math> and <math>r_i</math> be the center and radius of <math>\omega_i</math>, and let <math>O</math> and <math>r</math> be the center and radius of <math>\omega</math>. | ||
| Line 41: | Line 55: | ||
</asy> | </asy> | ||
| − | Since <math>X</math> is on the radical axis of <math>\omega_1</math> and <math>\omega_2</math>, it has equal power, so | + | Since <math>X</math> is on the radical axis of <math>\omega_1</math> and <math>\omega_2</math>, it has equal power with respect to both circles, so |
<cmath> O_1X^2 - r_1^2 = O_2X^2-r_2^2 \implies O_1X-O_2X = \frac{r_1^2-r_2^2}{d} </cmath>since <math>O_1X+O_2X=d</math>. Now we can solve for <math>O_1X</math> and <math>O_2X</math>, and in particular, | <cmath> O_1X^2 - r_1^2 = O_2X^2-r_2^2 \implies O_1X-O_2X = \frac{r_1^2-r_2^2}{d} </cmath>since <math>O_1X+O_2X=d</math>. Now we can solve for <math>O_1X</math> and <math>O_2X</math>, and in particular, | ||
<cmath>\begin{align*} | <cmath>\begin{align*} | ||
| Line 49: | Line 63: | ||
We want to solve for <math>d</math>. By the Pythagorean Theorem (twice): | We want to solve for <math>d</math>. By the Pythagorean Theorem (twice): | ||
<cmath>\begin{align*} | <cmath>\begin{align*} | ||
| − | &\qquad OH^2 = O_2H^2 - (r+r_2)^2 = O_1H^2 - (r+r_1)^2 \\ | + | &\qquad -OH^2 = O_2H^2 - (r+r_2)^2 = O_1H^2 - (r+r_1)^2 \\ |
&\implies \left(d+r-\tfrac{r_1^2-r_2^2}{d}\right)^2 - 4(r+r_2)^2 = \left(d-r+\tfrac{r_1^2-r_2^2}{d}\right)^2 - 4(r+r_1)^2 \\ | &\implies \left(d+r-\tfrac{r_1^2-r_2^2}{d}\right)^2 - 4(r+r_2)^2 = \left(d-r+\tfrac{r_1^2-r_2^2}{d}\right)^2 - 4(r+r_1)^2 \\ | ||
| − | &\implies 2dr - 2(r_1^2-r_2 | + | &\implies 2dr - 2(r_1^2-r_2^2)-8rr_2-4r_2^2 = -2dr+2(r_1^2-r_2^2)-8rr_1-4r_1^2 \\ |
&\implies 4dr = 8rr_2-8rr_1 \\ | &\implies 4dr = 8rr_2-8rr_1 \\ | ||
| − | &\implies | + | &\implies d=2r_2-2r_1 |
\end{align*}</cmath> | \end{align*}</cmath> | ||
Therefore, <math>d=2(r_2-r_1) = 2(961-625)=\boxed{672}</math>. | Therefore, <math>d=2(r_2-r_1) = 2(961-625)=\boxed{672}</math>. | ||
| − | ==See | + | ==Solution 2 (Linearity)== |
| + | Let <math>O_{1}</math>, <math>O_{2}</math>, and <math>O</math> be the centers of <math>\omega_{1}</math>, <math>\omega_{2}</math>, and <math>\omega</math> with <math>r_{1}</math>, <math>r_{2}</math>, and <math>r</math> their radii, respectively. Then, the distance from <math>O</math> to the radical axis <math>\ell\equiv\overline{AB}</math> of <math>\omega_{1}, \omega_{2}</math> is equal to <math>\frac{1}{2}r</math>. Let <math>x=O_{1}O_{2}</math> and <math>O^{\prime}</math> the orthogonal projection of <math>O</math> onto line <math>\ell</math>. Define the function <math>f:\mathbb{R}^{2}\rightarrow\mathbb{R}</math> by <cmath>f(X)=\text{Pow}_{\omega_{1}}(X)-\text{Pow}_{\omega_{2}}(X).</cmath> Then <cmath>\begin{align*} f(O_{1})=-r_{1}^{2}-(x-r_{2})(x+r_{2})&=-x^{2}+r_{2}^{2}-r_{1}^{2}, \\ f(O_{2})=(x-r_{1})(x+r_{1})-(-r_{2}^{2})&=x^{2}+r_{2}^{2}-r_{1}^{2}, \\ f(O)=r(r+2r_{1})-r(r+2r_{2})&=2r(r_{1}-r_{2}), \\ f(O^{\prime})&=0. \end{align*}</cmath> By [https://services.artofproblemsolving.com/download.php?id=YXR0YWNobWVudHMvMC84LzkzZjZjZmFlMGViY2E3MDMxNWQzY2IzNzFlZTk5NWFmOTM5ZGY1LnBkZg==&rn=TGluZWFyaXR5IG9mIFBvd2VyIG9mIGEgUG9pbnQucGRm linearity], <cmath>\frac{f(O_{2})-f(O_{1})}{f(O)-f(O^{\prime})}=\frac{O_{1}O_{2}}{OO^{\prime}}=\frac{x}{\tfrac{1}{2}r}=\frac{2x}{r}.</cmath> Notice that <math>f(O_{2})-f(O_{1})=x^{2}-(-x^{2})=2x^{2}</math> and <math>f(O)-f(O^{\prime})=2r(r_{1}-r_{2})</math>, thus <cmath>\begin{align*}\frac{2x^{2}}{2r(r_{1}-r_{2})}&=\frac{2x}{r}\end{align*}</cmath> Dividing both sides by <math>\frac{2x}{r}</math> (which is obviously nonzero as <math>x</math> is nonzero) gives us <cmath>\begin{align*}\frac{x}{2(r_{1}-r_{2})}&=1\end{align*}</cmath> so <math>x=2(r_{1}-r_{2})</math>. Since <math>r_{1}=961</math> and <math>r_{2}=625</math>, the answer is <math>x=2\cdot(961-625)=\boxed{672}</math>. | ||
| + | |||
| + | ==Solution 3== | ||
| + | Denote by <math>O_1</math>, <math>O_2</math>, and <math>O</math> the centers of <math>\omega_1</math>, <math>\omega_2</math>, and <math>\omega</math>, respectively. Let <math>R_1 = 961</math> and <math>R_2 = 625</math> denote the radii of <math>\omega_1</math> and <math>\omega_2</math> respectively, <math>r</math> be the radius of <math>\omega</math>, and <math>\ell</math> the distance from <math>O</math> to the line <math>AB</math>. We claim that<cmath>\dfrac{\ell}{r} = \dfrac{R_2-R_1}{d},</cmath>where <math>d = O_1O_2</math>. This solves the problem, for then the <math>\widehat{PQ} = 120^\circ</math> condition implies <math>\tfrac{\ell}r = \cos 60^\circ = \tfrac{1}{2}</math>, and then we can solve to get <math>d = \boxed{672}</math>. | ||
| + | <asy> | ||
| + | import olympiad; | ||
| + | size(230pt); | ||
| + | defaultpen(linewidth(0.8)+fontsize(10pt)); | ||
| + | real r1 = 17, r2 = 27, d = 35, r = 18; | ||
| + | pair O1 = origin, O2 = (d,0); | ||
| + | path w1 = circle(origin,r1), w2 = circle((d,0),r2), w1p = circle(origin,r1+r), w2p = circle((d,0), r2 + r); | ||
| + | pair[] X = intersectionpoints(w1,w2), Y = intersectionpoints(w1p,w2p); | ||
| + | pair O = Y[1]; | ||
| + | path w = circle(Y[1],r); | ||
| + | pair Xp = 5 * X[1] - 4 * X[0]; | ||
| + | pair[] P = intersectionpoints(Xp--X[0],w); | ||
| + | label("$O_1$",origin,N); | ||
| + | label("$O_2$",(d,0),N); | ||
| + | label("$O$",Y[1],SW); | ||
| + | draw(origin--Y[1]--(d,0)--cycle,gray(0.6)); | ||
| + | pair T = foot(O,O1,O2), Tp = foot(O,X[0],X[1]); | ||
| + | draw(Tp--O--T^^rightanglemark(O,T,O1,60)^^rightanglemark(O,Tp,X[0],60),gray(0.6)); | ||
| + | draw(w^^w1^^w2^^P[0]--X[0]); | ||
| + | dot(Y[1]^^origin^^(d,0)); | ||
| + | label("$X$",T,N,gray(0.6)); | ||
| + | label("$Y$",foot(X[0],O1,O2),NE,gray(0.6)); | ||
| + | label("$\ell$",(O+Tp)/2,S,gray(0.6)); | ||
| + | </asy> | ||
| + | |||
| + | Denote by <math>O_1</math> and <math>O_2</math> the centers of <math>\omega_1</math> and <math>\omega_2</math> respectively. Set <math>X</math> as the projection of <math>O</math> onto <math>O_1O_2</math>, and denote by <math>Y</math> the intersection of <math>AB</math> with <math>O_1O_2</math>. Note that <math>\ell = XY</math>. Now recall that<cmath>d(O_2Y-O_1Y) = O_2Y^2 - O_1Y^2 = R_2^2 - R_1^2.</cmath>Furthermore, note that<cmath>\begin{align*}d(O_2X - O_1X) &= O_2X^2 - O_1X^2= O_2O^2 - O_1O^2 \\ &= (R_2 + r)^2 - (R_1+r)^2 = (R_2^2 - R_1^2) + 2r(R_2 - R_1).\end{align*}</cmath>Substituting the first equality into the second one and subtracting yields<cmath>2r(R_2 - R_1) = d(O_2X - O_1X) - d(O_2Y - O_1Y) = 2dXY,</cmath>which rearranges to the desired. | ||
| + | |||
| + | ==Solution 4 (Quick)== | ||
| + | Suppose we label the points as shown [https://services.artofproblemsolving.com/download.php?id=YXR0YWNobWVudHMvNC9mLzRiM2JjYThjYmZlY2ViZGI0ODhjYzE4YzMyMmM0M2QyOTZlMmU5LmpwZw==&rn=MTU4ODUxMDg3XzczMDI0ODE4MTAwNjA5N184NDQzMjQxMjM3MDQ2NzQ5NjM4X24uanBn below]. | ||
| + | <asy> | ||
| + | defaultpen(fontsize(12)+0.6); size(300); | ||
| + | pen p=fontsize(10)+royalblue+0.4; | ||
| + | |||
| + | var r=1200; | ||
| + | pair O1=origin, O2=(672,0), O=OP(CR(O1,961+r),CR(O2,625+r)); | ||
| + | path c1=CR(O1,961), c2=CR(O2,625), c=CR(O,r); | ||
| + | pair | ||
| + | A=IP(CR(O1,961),CR(O2,625)), B=OP(CR(O1,961),CR(O2,625)), | ||
| + | P=IP(L(A,B,0,0.2),c), | ||
| + | Q=IP(L(A,B,0,200),c), | ||
| + | F=IP(CR(O,625+r),O--O1), | ||
| + | M=(F+O2)/2, | ||
| + | D=IP(CR(O,r),O--O1), | ||
| + | E=IP(CR(O,r),O--O2), | ||
| + | X=extension(E,D,O,O+O1-O2), | ||
| + | Y=extension(D,E,O1,O2); | ||
| + | |||
| + | draw(c1^^c2); draw(c,blue+0.6); draw(O1--O2--O--cycle,black+0.6); draw(O--X^^Y--O2,black+0.6); draw(X--Y,heavygreen+0.6); | ||
| + | draw((X+O)/2--O,MidArrow); draw(O2--Y-(300,0),MidArrow); | ||
| + | |||
| + | dot("$A$",A,dir(A-O2/2)); | ||
| + | dot("$B$",B,dir(B-O2/2)); | ||
| + | dot("$O_2$",O2,right+up); dot("$O_1$",O1,left+up); | ||
| + | dot("$O$",O,dir(O-O2)); | ||
| + | dot("$D$",D,dir(170)); | ||
| + | dot("$E$",E,dir(E-O1)); | ||
| + | dot("$X$",X,dir(X-D)); | ||
| + | dot("$Y$",Y,dir(Y-D)); | ||
| + | |||
| + | label("$R$",O--E,right+up,p); | ||
| + | label("$R$",O--D,left+down,p); | ||
| + | label("$2R$",(X+O)/2-(150,0),down,p); | ||
| + | label("$961$",O1--D,2*(left+down),p); | ||
| + | label("$625$",O2--E,2*(right+up),p); | ||
| + | |||
| + | MA("",E,D,O1,100,fuchsia+linewidth(1)); | ||
| + | MA("",X,D,O,100,fuchsia+linewidth(1)); | ||
| + | MA("",Y,E,O2,100,orange+linewidth(1)); | ||
| + | MA("",D,E,O,100,orange+linewidth(1)); | ||
| + | </asy> | ||
| + | By radical axis, the tangents to <math>\omega</math> at <math>D</math> and <math>E</math> intersect on <math>AB</math>. Thus <math>PDQE</math> is harmonic, so the tangents to <math>\omega</math> at <math>P</math> and <math>Q</math> intersect at <math>X \in DE</math>. Moreover, <math>OX \parallel O_1O_2</math> because both <math>OX</math> and <math>O_1O_2</math> are perpendicular to <math>AB</math>, and <math>OX = 2OP</math> because <math>\angle POQ = 120^{\circ}</math>. Thus<cmath>O_1O_2 = O_1Y - O_2Y = 2 \cdot 961 - 2\cdot 625 = \boxed{672}</cmath>by similar triangles. | ||
| + | |||
| + | ~mathman3880 | ||
| + | |||
| + | ==Solution 5 (Official MAA)== | ||
| + | Like in other solutions, let <math>O</math> be the center of <math>\omega</math> with <math>r</math> its radius; also, let <math>O_{1}</math> and <math>O_{2}</math> be the centers of <math>\omega_{1}</math> and <math>\omega_{2}</math> with <math>R_{1}</math> and <math>R_{2}</math> their radii, respectively. Let line <math>OP</math> intersect line <math>O_{1}O_{2}</math> at <math>T</math>, and let <math>u=TO_{2}</math>, <math>v=TO_{1}</math>, <math>x=PT</math>, where the length <math>O_{1}O_{2}</math> splits as <math>u+v</math>. Because the lines <math>PQ</math> and <math>O_{1}O_{2}</math> are perpendicular, lines <math>OT</math> and <math>O_{1}O_{2}</math> meet at a <math>60^{\circ}</math> angle. | ||
| + | |||
| + | Applying the Law of Cosines to <math>\triangle O_{2}PT</math>, <math>\triangle O_{1}PT</math>, <math>\triangle O_{2}OT</math>, and <math>\triangle O_{1}OT</math> gives <cmath>\begin{align*}\triangle O_{2}PT&:O_{2}P^{2}=u^{2}+x^{2}-ux \\ \triangle O_{1}PT&:O_{1}P^{2}=v^{2}+x^{2}+vx \\ \triangle O_{2}OT&:(r+R_{2})^{2}=u^{2}+(r+x)^{2}-u(r+x) \\ \triangle O_{1}OT&:(r+R_{1})^{2}=v^{2}+(r+x)^{2}+v(r+x)\end{align*}</cmath> | ||
| + | |||
| + | Adding the first and fourth equations, then subtracting the second and third equations gives us <cmath>\left(O_{2}P^{2}-O_{1}P^{2}\right)+\left(R_{1}^{2}-R_{2}^{2}\right)+2r(R_{1}-R_{2})=r(u+v)</cmath> | ||
| + | |||
| + | Since <math>P</math> lies on the radical axis of <math>\omega_{1}</math> and <math>\omega_{2}</math>, the power of point <math>P</math> with respect to either circle is <cmath>O_{2}P^{2}-R_{2}^{2}=O_{1}P^{2}-R_{1}^{2}.</cmath> | ||
| + | |||
| + | Hence <math>2r(R_{1}-R_{2})=r(u+v)</math> which simplifies to <cmath>u+v=2(R_{1}-R_{2}).</cmath> | ||
| + | |||
| + | The requested distance <cmath>O_{1}O_{2}=O_{1}T+O_{2}T=u+v</cmath> is therefore equal to <math>2\cdot(961-625)=\boxed{672}</math>. | ||
| + | |||
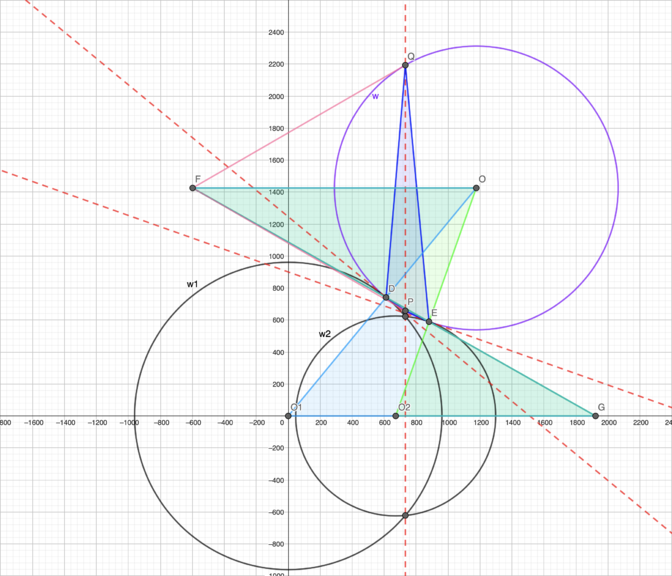
| + | ==Solution 6 (Geometry)== | ||
| + | [[File:2021 AIME I 13.png|500px|right]] | ||
| + | Let circle <math>\omega</math> tangent circles <math>\omega_1</math> and <math>\omega_2,</math> respectively at distinct points <math>C</math> and <math>D</math>. Let <math>O, O_1, O_2 (r, r_1, r_2)</math> be the centers (the radii) of <math>\omega, \omega_1</math> and <math>\omega_2,</math> respectively. WLOG <math>r_1 < r_2.</math> Let <math>F</math> be the point of <math>OO_2</math> such, that <math>OO_1 =OF.</math> Let <math>M</math> be the midpoint <math>FO_1, OE \perp AB, CT</math> be the radical axes of <math>\omega_1</math> and <math>\omega, T \in AB.</math> | ||
| + | |||
| + | Then <math>T</math> is radical center of <math>\omega, \omega_1</math> and <math>\omega_2, TD = CT.</math> | ||
| + | |||
| + | In <math>\triangle OFO_1 (OF = OO_1) OT</math> is bisector of <math>\angle O, OM</math> is median | ||
| + | |||
| + | <math>\hspace{10mm} \implies O,T,</math> and <math>M</math> are collinear. | ||
| + | |||
| + | <cmath>\angle OCT = \angle ODT = \angle OET = 90^\circ \implies</cmath> | ||
| + | |||
| + | <math>OCTDE</math> is cyclic (in <math>\Omega), OT</math> is diameter <math>\Omega.</math> | ||
| + | <math>O_1O_2 \perp AB, OM \perp FO_1 \implies \angle FO_1O_2 = \angle OTE</math> | ||
| + | <math>\angle OTE = \angle ODE</math> as they intercept the same arc <math> \overset{\Large\frown}{OE}</math> in <math>\Omega.</math> | ||
| + | <cmath>OE \perp AB, O_1O_2 \perp AB \implies O_1 O_2 || OE \implies</cmath> | ||
| + | <cmath>\angle OO_2O_1 = \angle O_2 OE \implies \triangle ODE \sim \triangle O_2 O_1 F \implies</cmath> | ||
| + | <cmath>\frac {OE}{OD} = \frac {O_2F}{O_1O_2} \implies \cos \frac {120^\circ}{2} = \frac{r_2 + r - r_1 -r} {O_1O_2}\implies {O_1O_2}= 2|r_2 – r_1|.</cmath> | ||
| + | |||
| + | Since <math>r_{1}=625</math> and <math>r_{2}=961</math>, the answer is <math>2\cdot|961-625|=\boxed{672}</math>. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Solution 7== | ||
| + | We are not given the radius of circle <math>w</math>, but based on the problem statement, that radius isn't important. We can set <math>w</math> to have radius infinity (solution 8), but if you didn't observe that, you could also set the radius to be <math>2r</math> so that the line containing the center of <math>w</math>, call it <math>W</math>, and <math>w_2</math>, call it <math>W_2</math>, is perpendicular to the line containing the center of <math>w_1</math>, call it <math>W_1</math> and <math>w_2</math>. Let <math>AB = 2h</math> and <math>W_1W_2 = x</math>. Also, let the projections of <math>W</math> and <math>W_1</math> onto line <math>AB</math> be <math>X</math> and <math>Y</math>, respectively. | ||
| + | |||
| + | By [[Pythagorean Theorem]] on <math>\triangle WW_1W_2</math>, we get | ||
| + | <cmath>x^2+(625+2x)^2=(961+2r)^2 \;(1)</cmath> | ||
| + | Note that since <math>\angle PWQ = 120</math>, <math>\angle PWX = 60</math>. So, <math>WX = 2r/2 = r = W_1Y</math>. We now get two more equations from Pythag: | ||
| + | <cmath>h^2+r^2 = 625^2 \; (2)</cmath> | ||
| + | <cmath>h^2+(x-r)^2 = 961^2 \; (3)</cmath> | ||
| + | From subtracting <math>(2)</math> and <math>(3)</math>, <math>x^2-2rx=961^2-625^2 \; (4)</math>. Rearranging <math>(3)</math> yields <math>x^2-1344r = 961^2+625^2</math>. Plugging in our result from <math>(4)</math>, <math>x^2-1344r= x^2-2rx \implies 1344r = 2rx \implies x=\boxed{672}</math>. | ||
| + | |||
| + | ~sml1809 | ||
| + | |||
| + | ==Solution 8 (Cheese)== | ||
| + | Let the [[circle]] <math>\omega</math> be infinitely big (a line). Then for it to be split into an [[arc]] of <math>120^{\circ}</math>, <math>\overline{PQ}</math> must intersect at a <math>60^{\circ}</math> with line <math>\omega</math>. | ||
| + | |||
| + | Notice the 30-60-90 triangle in the image. <math>O_1R = 961 - 625</math>. | ||
| + | |||
| + | Thus, the distance between the centers of <math>\omega_1</math> and <math>\omega_2</math> is <math>2(961-625)=\boxed{672}</math> | ||
| + | |||
| + | [[File:Cheesed circle.png|thumb|800px]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | picture by afly | ||
| + | |||
| + | ==Video Solution by MOP 2024== | ||
| + | https://youtu.be/GQT73xqvtXA | ||
| + | |||
| + | ~r00tsOfUnity | ||
| + | |||
| + | ==Video Solution== | ||
| + | https://youtu.be/gN7Ocu3D62M | ||
| + | |||
| + | ~Math Problem Solving Skills | ||
| + | |||
| + | ==Video Solution== | ||
| + | Who wanted to see animated video solutions can see this. I found this really helpful. | ||
| + | |||
| + | https://youtu.be/YtZ8_7i833E | ||
| + | |||
| + | P.S: This video is not made by me. And solution is same like below solutions. | ||
| + | |||
| + | ≈@rounak138 | ||
| + | |||
| + | ==See Also== | ||
{{AIME box|year=2021|n=I|num-b=12|num-a=14}} | {{AIME box|year=2021|n=I|num-b=12|num-a=14}} | ||
[[Category:Intermediate Geometry Problems]] | [[Category:Intermediate Geometry Problems]] | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 02:59, 7 February 2024
Contents
Problem
Circles ![]() and
and ![]() with radii
with radii ![]() and
and ![]() , respectively, intersect at distinct points
, respectively, intersect at distinct points ![]() and
and ![]() . A third circle
. A third circle ![]() is externally tangent to both
is externally tangent to both ![]() and
and ![]() . Suppose line
. Suppose line ![]() intersects
intersects ![]() at two points
at two points ![]() and
and ![]() such that the measure of minor arc
such that the measure of minor arc ![]() is
is ![]() . Find the distance between the centers of
. Find the distance between the centers of ![]() and
and ![]() .
.
Quick, Olympiad-Style Solution
Let ![]() and
and ![]() . The solution relies on the following key claim:
. The solution relies on the following key claim:
Claim. ![]() is a harmonic quadrilateral.
is a harmonic quadrilateral.
Proof. Using the radical axis theorem, the tangents to circle ![]() at
at ![]() and
and ![]() are concurrent with line
are concurrent with line ![]() at the radical center, implying that our claim is true by harmonic quadrilateral properties.
at the radical center, implying that our claim is true by harmonic quadrilateral properties. ![]()
Thus, we deduce the tangents to ![]() at
at ![]() and
and ![]() are concurrent at
are concurrent at ![]() with line
with line ![]() . Denote by
. Denote by ![]() the centers of
the centers of ![]() respectively.
respectively.
Now suppose ![]() . Note that
. Note that ![]() giving us the pairs of similar triangles
giving us the pairs of similar triangles ![]() We thereby obtain
We thereby obtain ![]() since
since ![]() , where
, where ![]() denotes the radius of
denotes the radius of ![]() , and
, and ![]() as well. It follows that
as well. It follows that ![]()
Solution 1 (Radical Axis)
Let ![]() and
and ![]() be the center and radius of
be the center and radius of ![]() , and let
, and let ![]() and
and ![]() be the center and radius of
be the center and radius of ![]() .
.
Since ![]() extends to an arc with arc
extends to an arc with arc ![]() , the distance from
, the distance from ![]() to
to ![]() is
is ![]() . Let
. Let ![]() . Consider
. Consider ![]() . The line
. The line ![]() is perpendicular to
is perpendicular to ![]() and passes through
and passes through ![]() . Let
. Let ![]() be the foot from
be the foot from ![]() to
to ![]() ; so
; so ![]() . We have by tangency
. We have by tangency ![]() and
and ![]() . Let
. Let ![]() .
.
![[asy] unitsize(3cm); pointpen=black; pointfontpen=fontsize(9); pair A=dir(110), B=dir(230), C=dir(310); DPA(A--B--C--A); pair H = foot(A, B, C); draw(A--H); pair X = 0.3*B + 0.7*C; pair Y = A+X-H; draw(X--1.3*Y-0.3*X); draw(A--Y, dotted); pair R1 = 1.3*X-0.3*Y; pair R2 = 0.7*X+0.3*Y; draw(R1--X); D("O",A,dir(A)); D("O_1",B,dir(B)); D("O_2",C,dir(C)); D("H",H,dir(270)); D("X",X,dir(225)); D("A",R1,dir(180)); D("B",R2,dir(180)); draw(rightanglemark(Y,X,C,3)); [/asy]](http://latex.artofproblemsolving.com/c/9/5/c95b22c0959ba5c836765acce30c45b25f1ec9f7.png) Since
Since ![]() is on the radical axis of
is on the radical axis of ![]() and
and ![]() , it has equal power with respect to both circles, so
, it has equal power with respect to both circles, so
![]() since
since ![]() . Now we can solve for
. Now we can solve for ![]() and
and ![]() , and in particular,
, and in particular,
 We want to solve for
We want to solve for ![]() . By the Pythagorean Theorem (twice):
. By the Pythagorean Theorem (twice):
 Therefore,
Therefore, ![]() .
.
Solution 2 (Linearity)
Let ![]() ,
, ![]() , and
, and ![]() be the centers of
be the centers of ![]() ,
, ![]() , and
, and ![]() with
with ![]() ,
, ![]() , and
, and ![]() their radii, respectively. Then, the distance from
their radii, respectively. Then, the distance from ![]() to the radical axis
to the radical axis ![]() of
of ![]() is equal to
is equal to ![]() . Let
. Let ![]() and
and ![]() the orthogonal projection of
the orthogonal projection of ![]() onto line
onto line ![]() . Define the function
. Define the function ![]() by
by ![]() Then
Then  By linearity,
By linearity, ![]() Notice that
Notice that ![]() and
and ![]() , thus
, thus ![]() Dividing both sides by
Dividing both sides by ![]() (which is obviously nonzero as
(which is obviously nonzero as ![]() is nonzero) gives us
is nonzero) gives us ![]() so
so ![]() . Since
. Since ![]() and
and ![]() , the answer is
, the answer is ![]() .
.
Solution 3
Denote by ![]() ,
, ![]() , and
, and ![]() the centers of
the centers of ![]() ,
, ![]() , and
, and ![]() , respectively. Let
, respectively. Let ![]() and
and ![]() denote the radii of
denote the radii of ![]() and
and ![]() respectively,
respectively, ![]() be the radius of
be the radius of ![]() , and
, and ![]() the distance from
the distance from ![]() to the line
to the line ![]() . We claim that
. We claim that![]() where
where ![]() . This solves the problem, for then the
. This solves the problem, for then the ![]() condition implies
condition implies ![]() , and then we can solve to get
, and then we can solve to get ![]() .
.
![[asy] import olympiad; size(230pt); defaultpen(linewidth(0.8)+fontsize(10pt)); real r1 = 17, r2 = 27, d = 35, r = 18; pair O1 = origin, O2 = (d,0); path w1 = circle(origin,r1), w2 = circle((d,0),r2), w1p = circle(origin,r1+r), w2p = circle((d,0), r2 + r); pair[] X = intersectionpoints(w1,w2), Y = intersectionpoints(w1p,w2p); pair O = Y[1]; path w = circle(Y[1],r); pair Xp = 5 * X[1] - 4 * X[0]; pair[] P = intersectionpoints(Xp--X[0],w); label("$O_1$",origin,N); label("$O_2$",(d,0),N); label("$O$",Y[1],SW); draw(origin--Y[1]--(d,0)--cycle,gray(0.6)); pair T = foot(O,O1,O2), Tp = foot(O,X[0],X[1]); draw(Tp--O--T^^rightanglemark(O,T,O1,60)^^rightanglemark(O,Tp,X[0],60),gray(0.6)); draw(w^^w1^^w2^^P[0]--X[0]); dot(Y[1]^^origin^^(d,0)); label("$X$",T,N,gray(0.6)); label("$Y$",foot(X[0],O1,O2),NE,gray(0.6)); label("$\ell$",(O+Tp)/2,S,gray(0.6)); [/asy]](http://latex.artofproblemsolving.com/0/e/8/0e8e58749647a67a085c53c6a9941b5e949fe1d9.png)
Denote by ![]() and
and ![]() the centers of
the centers of ![]() and
and ![]() respectively. Set
respectively. Set ![]() as the projection of
as the projection of ![]() onto
onto ![]() , and denote by
, and denote by ![]() the intersection of
the intersection of ![]() with
with ![]() . Note that
. Note that ![]() . Now recall that
. Now recall that![]() Furthermore, note that
Furthermore, note that![]() Substituting the first equality into the second one and subtracting yields
Substituting the first equality into the second one and subtracting yields![]() which rearranges to the desired.
which rearranges to the desired.
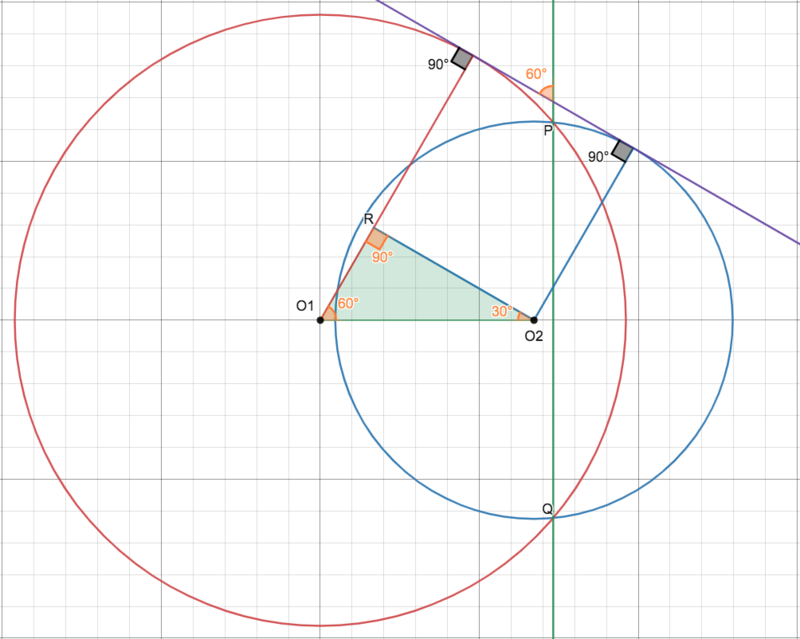
Solution 4 (Quick)
Suppose we label the points as shown below.
![[asy] defaultpen(fontsize(12)+0.6); size(300); pen p=fontsize(10)+royalblue+0.4; var r=1200; pair O1=origin, O2=(672,0), O=OP(CR(O1,961+r),CR(O2,625+r)); path c1=CR(O1,961), c2=CR(O2,625), c=CR(O,r); pair A=IP(CR(O1,961),CR(O2,625)), B=OP(CR(O1,961),CR(O2,625)), P=IP(L(A,B,0,0.2),c), Q=IP(L(A,B,0,200),c), F=IP(CR(O,625+r),O--O1), M=(F+O2)/2, D=IP(CR(O,r),O--O1), E=IP(CR(O,r),O--O2), X=extension(E,D,O,O+O1-O2), Y=extension(D,E,O1,O2); draw(c1^^c2); draw(c,blue+0.6); draw(O1--O2--O--cycle,black+0.6); draw(O--X^^Y--O2,black+0.6); draw(X--Y,heavygreen+0.6); draw((X+O)/2--O,MidArrow); draw(O2--Y-(300,0),MidArrow); dot("$A$",A,dir(A-O2/2)); dot("$B$",B,dir(B-O2/2)); dot("$O_2$",O2,right+up); dot("$O_1$",O1,left+up); dot("$O$",O,dir(O-O2)); dot("$D$",D,dir(170)); dot("$E$",E,dir(E-O1)); dot("$X$",X,dir(X-D)); dot("$Y$",Y,dir(Y-D)); label("$R$",O--E,right+up,p); label("$R$",O--D,left+down,p); label("$2R$",(X+O)/2-(150,0),down,p); label("$961$",O1--D,2*(left+down),p); label("$625$",O2--E,2*(right+up),p); MA("",E,D,O1,100,fuchsia+linewidth(1)); MA("",X,D,O,100,fuchsia+linewidth(1)); MA("",Y,E,O2,100,orange+linewidth(1)); MA("",D,E,O,100,orange+linewidth(1)); [/asy]](http://latex.artofproblemsolving.com/e/a/f/eaf558fcf764161f0c18bde0cf2949afb2a0d434.png) By radical axis, the tangents to
By radical axis, the tangents to ![]() at
at ![]() and
and ![]() intersect on
intersect on ![]() . Thus
. Thus ![]() is harmonic, so the tangents to
is harmonic, so the tangents to ![]() at
at ![]() and
and ![]() intersect at
intersect at ![]() . Moreover,
. Moreover, ![]() because both
because both ![]() and
and ![]() are perpendicular to
are perpendicular to ![]() , and
, and ![]() because
because ![]() . Thus
. Thus![]() by similar triangles.
by similar triangles.
~mathman3880
Solution 5 (Official MAA)
Like in other solutions, let ![]() be the center of
be the center of ![]() with
with ![]() its radius; also, let
its radius; also, let ![]() and
and ![]() be the centers of
be the centers of ![]() and
and ![]() with
with ![]() and
and ![]() their radii, respectively. Let line
their radii, respectively. Let line ![]() intersect line
intersect line ![]() at
at ![]() , and let
, and let ![]() ,
, ![]() ,
, ![]() , where the length
, where the length ![]() splits as
splits as ![]() . Because the lines
. Because the lines ![]() and
and ![]() are perpendicular, lines
are perpendicular, lines ![]() and
and ![]() meet at a
meet at a ![]() angle.
angle.
Applying the Law of Cosines to ![]() ,
, ![]() ,
, ![]() , and
, and ![]() gives
gives 
Adding the first and fourth equations, then subtracting the second and third equations gives us ![]()
Since ![]() lies on the radical axis of
lies on the radical axis of ![]() and
and ![]() , the power of point
, the power of point ![]() with respect to either circle is
with respect to either circle is ![]()
Hence ![]() which simplifies to
which simplifies to ![]()
The requested distance ![]() is therefore equal to
is therefore equal to ![]() .
.
Solution 6 (Geometry)
Let circle ![]() tangent circles
tangent circles ![]() and
and ![]() respectively at distinct points
respectively at distinct points ![]() and
and ![]() . Let
. Let ![]() be the centers (the radii) of
be the centers (the radii) of ![]() and
and ![]() respectively. WLOG
respectively. WLOG ![]() Let
Let ![]() be the point of
be the point of ![]() such, that
such, that ![]() Let
Let ![]() be the midpoint
be the midpoint ![]() be the radical axes of
be the radical axes of ![]() and
and ![]()
Then ![]() is radical center of
is radical center of ![]() and
and ![]()
In ![]() is bisector of
is bisector of ![]() is median
is median
![]() and
and ![]() are collinear.
are collinear.
![]()
![]() is cyclic (in
is cyclic (in ![]() is diameter
is diameter ![]()
![]()
![]() as they intercept the same arc
as they intercept the same arc ![]() in
in ![]()
![]()
![]()
![]()
Since ![]() and
and ![]() , the answer is
, the answer is ![]() .
.
vladimir.shelomovskii@gmail.com, vvsss
Solution 7
We are not given the radius of circle ![]() , but based on the problem statement, that radius isn't important. We can set
, but based on the problem statement, that radius isn't important. We can set ![]() to have radius infinity (solution 8), but if you didn't observe that, you could also set the radius to be
to have radius infinity (solution 8), but if you didn't observe that, you could also set the radius to be ![]() so that the line containing the center of
so that the line containing the center of ![]() , call it
, call it ![]() , and
, and ![]() , call it
, call it ![]() , is perpendicular to the line containing the center of
, is perpendicular to the line containing the center of ![]() , call it
, call it ![]() and
and ![]() . Let
. Let ![]() and
and ![]() . Also, let the projections of
. Also, let the projections of ![]() and
and ![]() onto line
onto line ![]() be
be ![]() and
and ![]() , respectively.
, respectively.
By Pythagorean Theorem on ![]() , we get
, we get
![]() Note that since
Note that since ![]() ,
, ![]() . So,
. So, ![]() . We now get two more equations from Pythag:
. We now get two more equations from Pythag:
![]()
![]() From subtracting
From subtracting ![]() and
and ![]() ,
, ![]() . Rearranging
. Rearranging ![]() yields
yields ![]() . Plugging in our result from
. Plugging in our result from ![]() ,
, ![]() .
.
~sml1809
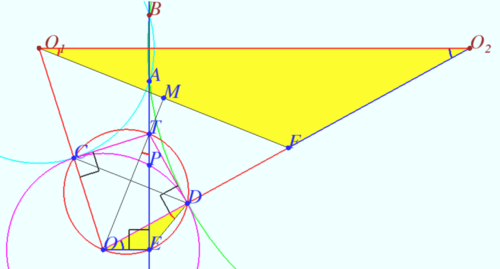
Solution 8 (Cheese)
Let the circle ![]() be infinitely big (a line). Then for it to be split into an arc of
be infinitely big (a line). Then for it to be split into an arc of ![]() ,
, ![]() must intersect at a
must intersect at a ![]() with line
with line ![]() .
.
Notice the 30-60-90 triangle in the image. ![]() .
.
Thus, the distance between the centers of ![]() and
and ![]() is
is ![]()
picture by afly
Video Solution by MOP 2024
~r00tsOfUnity
Video Solution
~Math Problem Solving Skills
Video Solution
Who wanted to see animated video solutions can see this. I found this really helpful.
P.S: This video is not made by me. And solution is same like below solutions.
≈@rounak138
See Also
| 2021 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 12 |
Followed by Problem 14 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.