Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2022 USAMO Problems/Problem 2"

m (→‎Solution)
(→‎Solution 2)
 
(8 intermediate revisions by 5 users not shown)
Line 67: Line 67:
 
Prove that the difference of the areas of <math>B</math> and <math>W</math> depends only on the numbers <math>b</math> and <math>w</math>, and not on how the <math>2n</math>-gon was assembled.
 
Prove that the difference of the areas of <math>B</math> and <math>W</math> depends only on the numbers <math>b</math> and <math>w</math>, and not on how the <math>2n</math>-gon was assembled.
  
−
==Solution==
+
 
 +
 
 +
==Solution 1==
 
First notice that the black rods and the white rods form polygons iff in the original <math>2n</math>-gon, if a side is a color <math>x</math>, then the side that is parallel to that side in the original <math>2n</math>-gon is also the color <math>x</math>.  
 
First notice that the black rods and the white rods form polygons iff in the original <math>2n</math>-gon, if a side is a color <math>x</math>, then the side that is parallel to that side in the original <math>2n</math>-gon is also the color <math>x</math>.  
  
−
We can to prove that the difference in areas is only affected by the values of <math>b</math> and <math>w</math> by showing that for any valid arrangement of <math>2b</math> rods and <math>2w</math> rods, we may switch any two adjacent black and white rods(and their "parallel pairs"), and end up with the same area difference as we originally started with.  
+
We can prove that the difference in areas is only affected by the values of <math>b</math> and <math>w</math> by showing that for any valid arrangement of <math>2b</math> rods and <math>2w</math> rods, we may switch any two adjacent black and white rods(and their "parallel pairs"), and end up with the same area difference.  
  
−
Figure link: media.discordapp.net/attachments/909142407797428324/1064711986849521735/image0.jpg?
+
[[File:Peppa-usamo-2022-2.png|800px]]
  
−
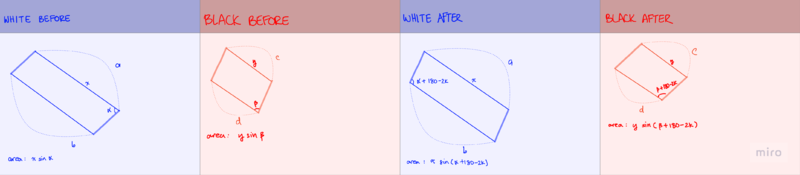
In the figure above, after the switch, we can see that after removing the mutually congruent parts, we are left with two parallelograms from each color. Let <math>x</math>, <math>\alpha{}</math>, <math>y</math>, and <math>\beta{}</math> be defined as shown. Notice that if we angle chase, the sides of the other parallelogram are the same, but if the angles of the original <math>2n</math>-gon all have measure <math>2k</math>, the angles of the new parallelograms are <math>\alpha{}+180-2k</math> and <math>\beta{}+180-2k</math>, as shown. We must prove that the differences between the areas are the same.  
+
In the figure above (click to expand), after the switch, we can see that after removing the mutually congruent parts, we are left with two parallelograms from each color. Let <math>x</math>, <math>\alpha{}</math>, <math>y</math>, and <math>\beta{}</math> be defined as shown. Notice that if we angle chase, the sides of the other parallelogram are the same, but if the angles of the original <math>2n</math>-gon all have measure <math>2k</math>, the angles of the new parallelograms are <math>\alpha{}+180-2k</math> and <math>\beta{}+180-2k</math>, as shown. We must prove that the differences between the areas are the same.  
  
−
Using area formulas, we are left with proving that <math>x\sin{\alpha{}}-y\sin{\beta{}}+y\sin{(2k-\beta{})}-x\sin{(2k-\alpha{})}</math>, which is equal to <math>\sin{k}(2\cos^2{k})-2\sin{k}\cos{k}\cos{\alpha{}}-\sin{k}(2\cos^2{k})+\sin{k}\cos{k}\cos{\beta{}}</math>, or <math>2\cos{k}(x\sin{(\alpha{}-k)}+y\sin{(k-\beta{}}))</math>. Since <math>\cos{k}</math> is not <math>0</math> because <math>n\geq{}3</math>, we are left with proving that <math>x\sin{(\alpha{}-k)}+y\sin{(k-\beta{}})=0</math>
+
Using area formulas, the change in the difference of areas is <math>x\sin{\alpha{}}-y\sin{\beta{}}+y\sin{(2k-\beta{})}-x\sin{(2k-\alpha{})}</math>, which is equal to <math>x(\sin{k}(2\cos^2{k})-2\sin{k}\cos{k}\cos{\alpha{}})-y(\sin{k}(2\cos^2{k}))+y(\sin{k}\cos{k}\cos{\beta{}})</math>, or <math>2\cos{k}(x\sin{(\alpha{}-k)}+y\sin{(k-\beta{}}))</math>. Since <math>\cos{k}</math> is not <math>0</math> because <math>n\geq{}3</math>, we are left with proving that <math>x\sin{(\alpha{}-k)}+y\sin{(k-\beta{}})=0</math>.
  
 
Now we rotate the polygon so that the vertex between the two sides that we switched is at the point <math>(0,0)</math>, the angle bisector of that vertex is <math>y=0</math>, and the black side is in the positive <math>y</math>-direction. Now think of all the sides as vectors, all pointing in the clockwise direction of the <math>2n</math>-gon.
 
Now we rotate the polygon so that the vertex between the two sides that we switched is at the point <math>(0,0)</math>, the angle bisector of that vertex is <math>y=0</math>, and the black side is in the positive <math>y</math>-direction. Now think of all the sides as vectors, all pointing in the clockwise direction of the <math>2n</math>-gon.
Line 85: Line 87:
  
 
~by @peppapig_
 
~by @peppapig_
 +
 +
 +
 +
==Solution 2==
 +
Pick a pair of parallel sides of the regular <math>2n</math>-gon and flip their color. Let those two lines be the horizontal. The area of the polygon formed by rods of the original color decreases by a parallelogram with height equal to the sum of the vertical heights of the rods of that color divided by <math>2</math> and base length <math>1</math>. Similarly, the area of the polygon formed by rods of the new color increases by the sum of the vertical heights of the rods of the new color divided by <math>2</math>. The sum of the heights of all the rod is equal to twice the height of the <math>2n</math>-gon, so the difference between the areas of <math>B</math> and <math>W</math> changes by the height of the <math>2n</math>-gon, which is fixed when <math>n</math> is fixed.
 +
 +
If we pair two pairs different-colored pairs of parallel sides of the <math>2n</math>-gon and flip the colors of both pairs, then <math>b</math> and <math>w</math> and the difference in the areas of <math>B</math> and <math>W</math> will remain unchanged. Thus, the difference in the areas of <math>B</math> and <math>W</math> depends only on <math>b</math> and <math>w</math>.
  
 
==See also==
 
==See also==
 
{{USAMO newbox|year=2022|num-b=1|num-a=3}}
 
{{USAMO newbox|year=2022|num-b=1|num-a=3}}
 +
{{USAJMO newbox|year=2022|num-b=2|num-a=4}}
 +
{{MAA Notice}}
 +
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 01:08, 9 January 2024

Problem

Let $b\geq2$ and $w\geq2$ be fixed integers, and $n=b+w$. Given are $2b$ identical black rods and $2w$ identical white rods, each of side length $1$.

We assemble a regular $2n$-gon using these rods so that parallel sides are the same color. Then, a convex $2b$-gon $B$ is formed by translating the black rods, and a convex $2w$-gon $W$ is formed by translating the white rods. An example of one way of doing the assembly when $b=3$ and $w=2$ is shown below, as well as the resulting polygons $B$ and $W$.

[asy] size(10cm); real w = 2*Sin(18); real h = 0.10 * w; real d = 0.33 * h; picture wht; picture blk; draw(wht, (0,0)--(w,0)--(w+d,h)--(-d,h)--cycle); fill(blk, (0,0)--(w,0)--(w+d,h)--(-d,h)--cycle, black); // draw(unitcircle, blue+dotted); // Original polygon add(shift(dir(108))*blk); add(shift(dir(72))*rotate(324)*blk); add(shift(dir(36))*rotate(288)*wht); add(shift(dir(0))*rotate(252)*blk); add(shift(dir(324))*rotate(216)*wht); add(shift(dir(288))*rotate(180)*blk); add(shift(dir(252))*rotate(144)*blk); add(shift(dir(216))*rotate(108)*wht); add(shift(dir(180))*rotate(72)*blk); add(shift(dir(144))*rotate(36)*wht); // White shifted real Wk = 1.2; pair W1 = (1.8,0.1); pair W2 = W1 + w*dir(36); pair W3 = W2 + w*dir(108); pair W4 = W3 + w*dir(216); path Wgon = W1--W2--W3--W4--cycle; draw(Wgon); pair WO = (W1+W3)/2; transform Wt = shift(WO)*scale(Wk)*shift(-WO); draw(Wt * Wgon); label("$W$", WO); /* draw(W1--Wt*W1); draw(W2--Wt*W2); draw(W3--Wt*W3); draw(W4--Wt*W4); */ // Black shifted real Bk = 1.10; pair B1 = (1.5,-0.1); pair B2 = B1 + w*dir(0); pair B3 = B2 + w*dir(324); pair B4 = B3 + w*dir(252); pair B5 = B4 + w*dir(180); pair B6 = B5 + w*dir(144); path Bgon = B1--B2--B3--B4--B5--B6--cycle; pair BO = (B1+B4)/2; transform Bt = shift(BO)*scale(Bk)*shift(-BO); fill(Bt * Bgon, black); fill(Bgon, white); label("$B$", BO); [/asy]

Prove that the difference of the areas of $B$ and $W$ depends only on the numbers $b$ and $w$, and not on how the $2n$-gon was assembled.


Solution 1

First notice that the black rods and the white rods form polygons iff in the original $2n$-gon, if a side is a color $x$, then the side that is parallel to that side in the original $2n$-gon is also the color $x$.

We can prove that the difference in areas is only affected by the values of $b$ and $w$ by showing that for any valid arrangement of $2b$ rods and $2w$ rods, we may switch any two adjacent black and white rods(and their "parallel pairs"), and end up with the same area difference.

Peppa-usamo-2022-2.png

In the figure above (click to expand), after the switch, we can see that after removing the mutually congruent parts, we are left with two parallelograms from each color. Let $x$, $\alpha{}$, $y$, and $\beta{}$ be defined as shown. Notice that if we angle chase, the sides of the other parallelogram are the same, but if the angles of the original $2n$-gon all have measure $2k$, the angles of the new parallelograms are $\alpha{}+180-2k$ and $\beta{}+180-2k$, as shown. We must prove that the differences between the areas are the same.

Using area formulas, the change in the difference of areas is $x\sin{\alpha{}}-y\sin{\beta{}}+y\sin{(2k-\beta{})}-x\sin{(2k-\alpha{})}$, which is equal to $x(\sin{k}(2\cos^2{k})-2\sin{k}\cos{k}\cos{\alpha{}})-y(\sin{k}(2\cos^2{k}))+y(\sin{k}\cos{k}\cos{\beta{}})$, or $2\cos{k}(x\sin{(\alpha{}-k)}+y\sin{(k-\beta{}}))$. Since $\cos{k}$ is not $0$ because $n\geq{}3$, we are left with proving that $x\sin{(\alpha{}-k)}+y\sin{(k-\beta{}})=0$.

Now we rotate the polygon so that the vertex between the two sides that we switched is at the point $(0,0)$, the angle bisector of that vertex is $y=0$, and the black side is in the positive $y$-direction. Now think of all the sides as vectors, all pointing in the clockwise direction of the $2n$-gon.

Notice the part labeled $a$ in the black polygons. We have that the vector labeled $x$ is really just the sum of all of the vectors in the part labeled $a$ - or all the vectors in the $2n$-gon that are in the positive $y$-direction excluding the one that was interchanged. Also notice that the angle of this vector $x$ has a signed angle of $\alpha{}-k$ with $y=0$ and has length $x$ - meaning that the vertical displacement of the vector $x$ from $y=0$ is equal to $x\sin{(\alpha{}-k)}$! Similarly, we get that the vertical displacement of the vector $y$ is equivalent to $y\sin{(k-\beta{}})$.

Adding these two together, we get that $x\sin{(\alpha{}-k)}+y\sin{(k-\beta{}})$ is simply the vertical displacement of the sum of the vectors $x$ and $y$. Since the sum of the vectors $x$ and $y$ is equivalent to the sum of the vectors in the positive half of the polygon minus the sum of the black vector that would be switched with the white vector(the leftmost vector in the positive half of the polygon) and the rightmost vector in the positive half(which is the parallel pair of the white vector that would be interchanged later), and we know that this sum happens to have a vertical displacement of $0$, along with the fact that the positive half of the polygon summed together also has a vertical displacement of $0$, we get that the total vertical displacement is $0$, meaning that $x\sin{(\alpha{}-k)}+y\sin{(k-\beta{}})=0$, and we are done.

~by @peppapig_


Solution 2

Pick a pair of parallel sides of the regular $2n$-gon and flip their color. Let those two lines be the horizontal. The area of the polygon formed by rods of the original color decreases by a parallelogram with height equal to the sum of the vertical heights of the rods of that color divided by $2$ and base length $1$. Similarly, the area of the polygon formed by rods of the new color increases by the sum of the vertical heights of the rods of the new color divided by $2$. The sum of the heights of all the rod is equal to twice the height of the $2n$-gon, so the difference between the areas of $B$ and $W$ changes by the height of the $2n$-gon, which is fixed when $n$ is fixed.

If we pair two pairs different-colored pairs of parallel sides of the $2n$-gon and flip the colors of both pairs, then $b$ and $w$ and the difference in the areas of $B$ and $W$ will remain unchanged. Thus, the difference in the areas of $B$ and $W$ depends only on $b$ and $w$.

See also

2022 USAMO (Problems • Resources)
Preceded by
Problem 1 		Followed by
Problem 3
1 • 2 • 3 • 4 • 5 • 6
All USAMO Problems and Solutions
2022 USAJMO (Problems • Resources)
Preceded by
Problem 2 		Followed by
Problem 4
1 • 2 • 3 • 4 • 5 • 6
All USAJMO Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2022_USAMO_Problems/Problem_2&oldid=210318"