Difference between revisions of "2012 AMC 8 Problems/Problem 5"
(→Solution: That wasn't even a solution before.) |
Nishank seth (talk | contribs) m (→Solution 2) |
||
| (7 intermediate revisions by 4 users not shown) | |||
| Line 43: | Line 43: | ||
<math> \textbf{(A)}\hspace{.05in}1\qquad\textbf{(B)}\hspace{.05in}2\qquad\textbf{(C)}\hspace{.05in}3\qquad\textbf{(D)}\hspace{.05in}4\qquad\textbf{(E)}\hspace{.05in}5 </math> | <math> \textbf{(A)}\hspace{.05in}1\qquad\textbf{(B)}\hspace{.05in}2\qquad\textbf{(C)}\hspace{.05in}3\qquad\textbf{(D)}\hspace{.05in}4\qquad\textbf{(E)}\hspace{.05in}5 </math> | ||
| − | ==Solution== | + | ==Solution 1== |
[[File:2012amc85.png]] | [[File:2012amc85.png]] | ||
| − | + | ||
<math>1 + 1 + 1 + 2 + X = 1 + 2 + 1 + 6\\ | <math>1 + 1 + 1 + 2 + X = 1 + 2 + 1 + 6\\ | ||
| Line 52: | Line 52: | ||
Thus, the answer is <math> \boxed{\textbf{(E)}\ 5} </math>. | Thus, the answer is <math> \boxed{\textbf{(E)}\ 5} </math>. | ||
| + | |||
| + | ==Solution 2== | ||
| + | [[File:bcd57a9d78159bce4d3873f81f5d879beaed1d5a.png|300px|center]] | ||
| + | |||
| + | Note that we only need to consider the value below the marked red line, so we have the equation: | ||
| + | <cmath> X + 2 = 6 + 1 </cmath> | ||
| + | <cmath> X = 5 </cmath> | ||
| + | |||
| + | Hence, the answer is <math> \boxed{\textbf{(E)}\ 5} </math>. | ||
| + | |||
| + | ~[[User:Bloggish|Bloggish]] | ||
| + | |||
| + | ==Video Solution== | ||
| + | https://youtu.be/m4g-Nmot-c8 ~savannahsolver | ||
==See Also== | ==See Also== | ||
{{AMC8 box|year=2012|num-b=4|num-a=6}} | {{AMC8 box|year=2012|num-b=4|num-a=6}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 19:16, 3 January 2024
Problem
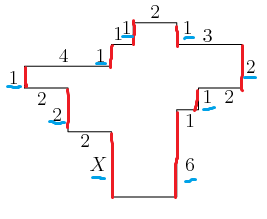
In the diagram, all angles are right angles and the lengths of the sides are given in centimeters. Note the diagram is not drawn to scale. What is , 
in centimeters?
![[asy] pair A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R; A=(4,0); B=(7,0); C=(7,4); D=(8,4); E=(8,5); F=(10,5); G=(10,7); H=(7,7); I=(7,8); J=(5,8); K=(5,7); L=(4,7); M=(4,6); N=(0,6); O=(0,5); P=(2,5); Q=(2,3); R=(4,3); draw(A--B--C--D--E--F--G--H--I--J--K--L--M--N--O--P--Q--R--cycle); label("$X$",(3.4,1.5)); label("6",(7.6,1.5)); label("1",(7.6,3.5)); label("1",(8.4,4.6)); label("2",(9.4,4.6)); label("2",(10.4,6)); label("3",(8.4,7.4)); label("1",(7.5,7.8)); label("2",(6,8.5)); label("1",(4.7,7.8)); label("1",(4.3,7.5)); label("1",(3.5,6.5)); label("4",(1.8,6.5)); label("1",(-0.5,5.5)); label("2",(0.8,4.5)); label("2",(1.5,3.8)); label("2",(2.8,2.6));[/asy]](http://latex.artofproblemsolving.com/b/c/d/bcd57a9d78159bce4d3873f81f5d879beaed1d5a.png)
Solution 1
Thus, the answer is 
.
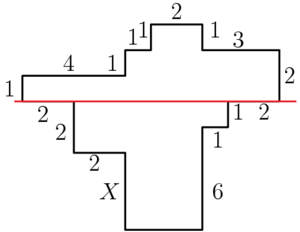
Solution 2
Note that we only need to consider the value below the marked red line, so we have the equation:
![\[X + 2 = 6 + 1\]](http://latex.artofproblemsolving.com/4/d/f/4df9ced0f2c10dfa5f6b6590a125d641804f37fc.png)
![\[X = 5\]](http://latex.artofproblemsolving.com/d/4/2/d428366384771ecc1c4a712b9898e2c680a889a8.png)
Hence, the answer is .
Video Solution
https://youtu.be/m4g-Nmot-c8 ~savannahsolver
See Also
| 2012 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 4 |
Followed by Problem 6 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
