Difference between revisions of "1992 OIM Problems/Problem 2"

Latest revision as of 08:42, 23 December 2023

Problem

Given the collection of $n$ positive real numbers $a_1 < a_2 < a_3 < \cdots < a_n$ and the function:

$f(x) = \frac{a_1}{x+a_1}+\frac{a_2}{x+a_2}+\cdots +\frac{a_n}{x+a_n}$

Determine the sum of the lengths of the intervals, disjoint two by two, formed by all $f(x) = 1$ .

~translated into English by Tomas Diaz. ~orders@tomasdiaz.com

Solution

Since $0<a_1 < a_2 < a_3 < \cdots < a_n$ , we can plot $f(x)$ to visualize what we're looking for:

Notice that the intervals will be: $I_1=r_1-(-a_1), I_2=r_2-(-a_2), \cdots , I_n=r_n-(-a_n)$

Thus the sum of the intervals will be: $\sum_{i}^{}\left( r_i+a_i \right)$

Now we set $f(x)=1$ :

$f(x)=\frac{\sum_{j\ne i}^{}\left( a_i \prod_{j}^{}\left(x+a_j \right)\right)}{\prod_{i}^{}\left( x+a_i\right)}=1$

And solve for zero:

$\prod_{i}^{}\left( x+a_i\right)-\sum_{j \ne i}^{}\left( a_i \prod_{j}^{}\left(x+a_j \right)\right)=0$

$\left( x^n+\sum_{i}^{}a_ix^{n-1}+K_{n-2}x^{n-2}+\cdots+K_1x+K_0\right)-\left( \sum_{i}^{}a_ix^{n-1}+L_{n-2}x^{n-2}+\cdots+L_1x+L_0\right)=0$

$x^n+\left( \sum_{i}^{}a_i-\sum_{i}^{}a_i \right)x^{n-1}+\left( K_{n-2}-L_{n-2} \right)x^{n-2}+\cdots+\left( K_{1}-L_{1} \right)x+\left( K_{0}-L_{0} \right)=0$

Where $K_i$ and $L_i$ are coefficients of the respective polynomials for each $x^i$

$x^n+(0)x^{n-1}+\left( K_{n-2}-L_{n-2} \right)x^{n-2}+\cdots+\left( K_{1}-L_{1} \right)x+\left( K_{0}-L_{0} \right)=0$

From properties of polynomials, we know that the sum of the roots of a polynomial of degree n is $-b/a$ where $b$ is the coefficient of $x^{n-1}$ and $a$ is the coefficient of $x^n$

Therefore, $\sum_{i}^{}r_i=-0/1=0$

and, $\sum_{i}^{}\left( r_i+a_i \right)=\sum_{i}^{}r_i+\sum_{i}^{}a_i=\sum_{i}^{}a_i$

Thus the sum of the intervals is $\sum_{i}^{}a_i$

Note. I actually competed at this event in Venezuela when I was in High School representing Puerto Rico. I got a ZERO on this one because I didn't even know what was I supposed to do, nor did I know what the sum of the lengths of the intervals, disjoint two by two meant. I didn't even get points for drawing the function. haha. Several decades ago I was able to finally solve it. But even now, I'm still unsure about the "disjunct two by two" wording...

~Tomas Diaz. ~orders@tomasdiaz.com

Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.

@@ Line 4: / Line 4: @@
 <cmath>f(x) = \frac{a_1}{x+a_1}+\frac{a_2}{x+a_2}+\cdots +\frac{a_n}{x+a_n} </cmath>
-Determine the sum of the lengths of the intervals, disjoint two by two, formed by all <math>x = 1</math>.
+Determine the sum of the lengths of the intervals, disjoint two by two, formed by all <math>f(x) = 1</math>.
 ~translated into English by Tomas Diaz. ~orders@tomasdiaz.com
 == Solution ==
-* Note.  I actually competed at this event in Venezuela when I was in High School representing Puerto Rico.  I got a ZERO on this one because I didn't even know what was I supposed to do, nor did I know what the sum of the lengths of the intervals, disjoint two by two meant.  A decade ago I finally solved it but now I don't remember how.  I will attempt to solve this one later.
-{{solution}}
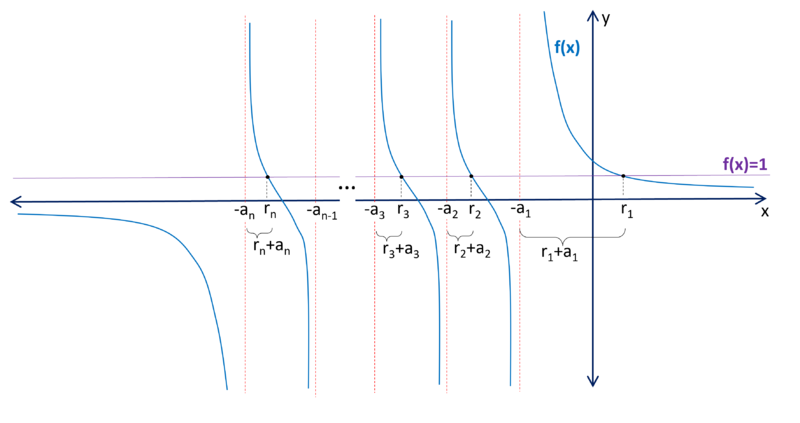
+Since <math>0<a_1 < a_2 < a_3 < \cdots < a_n</math>, we can plot <math>f(x)</math> to visualize what we're looking for:
+[[File:1992_OIM_P2b.png|center|800px]]
+Notice that the intervals will be: <math>I_1=r_1-(-a_1), I_2=r_2-(-a_2), \cdots , I_n=r_n-(-a_n)</math>
+Thus the sum of the intervals will be: <math>\sum_{i}^{}\left( r_i+a_i \right)</math>
+Now we set <math>f(x)=1</math>:
+<math>f(x)=\frac{\sum_{j\ne i}^{}\left( a_i \prod_{j}^{}\left(x+a_j  \right)\right)}{\prod_{i}^{}\left(  x+a_i\right)}=1</math>
+And solve for zero:
+<math>\prod_{i}^{}\left(  x+a_i\right)-\sum_{j \ne i}^{}\left( a_i \prod_{j}^{}\left(x+a_j  \right)\right)=0</math>
+<math>\left( x^n+\sum_{i}^{}a_ix^{n-1}+K_{n-2}x^{n-2}+\cdots+K_1x+K_0\right)-\left( \sum_{i}^{}a_ix^{n-1}+L_{n-2}x^{n-2}+\cdots+L_1x+L_0\right)=0</math>
+<math> x^n+\left( \sum_{i}^{}a_i-\sum_{i}^{}a_i \right)x^{n-1}+\left( K_{n-2}-L_{n-2} \right)x^{n-2}+\cdots+\left( K_{1}-L_{1} \right)x+\left( K_{0}-L_{0} \right)=0</math>
+Where <math>K_i</math> and <math>L_i</math> are coefficients of the respective polynomials for each <math>x^i</math>
+<math> x^n+(0)x^{n-1}+\left( K_{n-2}-L_{n-2} \right)x^{n-2}+\cdots+\left( K_{1}-L_{1} \right)x+\left( K_{0}-L_{0} \right)=0</math>
+From properties of polynomials, we know that the sum of the roots of a polynomial of degree n is <math>-b/a</math> where <math>b</math> is the coefficient of <math>x^{n-1}</math> and <math>a</math> is the coefficient of <math>x^n</math>
+Therefore, <math>\sum_{i}^{}r_i=-0/1=0</math>
+and, <math>\sum_{i}^{}\left( r_i+a_i \right)=\sum_{i}^{}r_i+\sum_{i}^{}a_i=\sum_{i}^{}a_i</math>
+Thus the sum of the intervals is <math>\sum_{i}^{}a_i</math>
+* Note.  I actually competed at this event in Venezuela when I was in High School representing Puerto Rico.  I got a ZERO on this one because I didn't even know what was I supposed to do, nor did I know what the sum of the lengths of the intervals, disjoint two by two meant.  I didn't even get points for drawing the function.  haha.  Several decades ago I was able to finally solve it.  But even now, I'm still unsure about the "disjunct two by two" wording...
+~Tomas Diaz. ~orders@tomasdiaz.com
+{{alternate solutions}}
 == See also ==
+[[OIM Problems and Solutions]]
 https://www.oma.org.ar/enunciados/ibe7.htm

Page

Toolbox

Search

Difference between revisions of "1992 OIM Problems/Problem 2"

Latest revision as of 08:42, 23 December 2023

Problem

Solution

See also