Difference between revisions of "1991 OIM Problems/Problem 2"
| Line 6: | Line 6: | ||
== Solution == | == Solution == | ||
[[File:1991_OIM_p2c.png|700px]] | [[File:1991_OIM_p2c.png|700px]] | ||
| + | |||
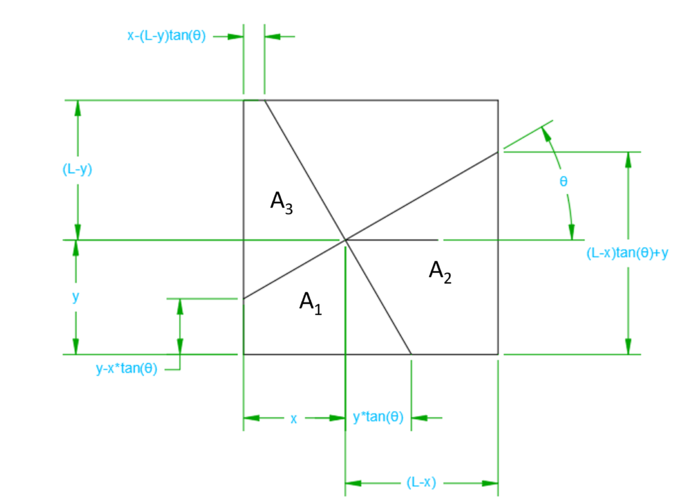
| + | First let's find the area of <math>A_1</math>: | ||
| + | |||
| + | <math>A_1=\frac{y-x.tan(\theta)+y}{2}+\frac{y}{y.tan(\theta)}{2}</math> | ||
* Note. I actually competed at this event in Argentina when I was in High School representing Puerto Rico. I got partial points because I couldn't prove this but had somewhat of an approach to get there. | * Note. I actually competed at this event in Argentina when I was in High School representing Puerto Rico. I got partial points because I couldn't prove this but had somewhat of an approach to get there. | ||
Revision as of 23:20, 22 December 2023
Problem
Two perpendicular lines divide a square into four parts, three of which each have an area equal to 1. Show that the area of the square is four.
~translated into English by Tomas Diaz. ~orders@tomasdiaz.com
Solution
First let's find the area of ![]() :
:
![]()
- Note. I actually competed at this event in Argentina when I was in High School representing Puerto Rico. I got partial points because I couldn't prove this but had somewhat of an approach to get there.
~Tomas Diaz. orders@tomasdiaz.com
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.