Difference between revisions of "1992 OIM Problems/Problem 2"
| Line 23: | Line 23: | ||
And solve for zero: | And solve for zero: | ||
| − | <math>\sum_{j\ne i}^{}\left( a_i \prod_{j}^{}\left(x+a_j \right)\right) | + | <math>\sum_{j \ne i}^{}\left( a_i \prod_{j}^{}\left(x+a_j \right)\right)-\prod_{i}^{}\left( x+a_i\right)=0</math> |
* Note. I actually competed at this event in Venezuela when I was in High School representing Puerto Rico. I got a ZERO on this one because I didn't even know what was I supposed to do, nor did I know what the sum of the lengths of the intervals, disjoint two by two meant. A decade ago I finally solved it but now I don't remember how. I will attempt to solve this one later. | * Note. I actually competed at this event in Venezuela when I was in High School representing Puerto Rico. I got a ZERO on this one because I didn't even know what was I supposed to do, nor did I know what the sum of the lengths of the intervals, disjoint two by two meant. A decade ago I finally solved it but now I don't remember how. I will attempt to solve this one later. | ||
Revision as of 11:13, 17 December 2023
Problem
Given the collection of ![]() positive real numbers
positive real numbers ![]() and the function:
and the function:
![]()
Determine the sum of the lengths of the intervals, disjoint two by two, formed by all ![]() .
.
~translated into English by Tomas Diaz. ~orders@tomasdiaz.com
Solution
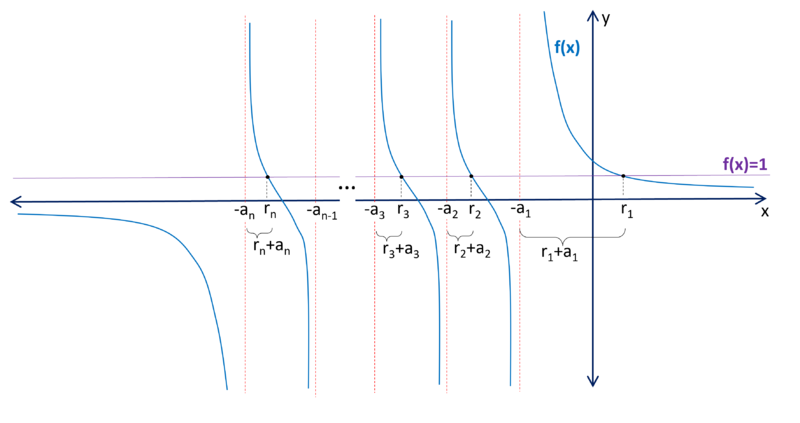
Since ![]() , we can plot
, we can plot ![]() to visualize what we're looking for:
to visualize what we're looking for:
Notice that the intervals will be: ![]()
Thus the sum of the intervals will be: ![]()
Now we set ![]() :
:

And solve for zero:

- Note. I actually competed at this event in Venezuela when I was in High School representing Puerto Rico. I got a ZERO on this one because I didn't even know what was I supposed to do, nor did I know what the sum of the lengths of the intervals, disjoint two by two meant. A decade ago I finally solved it but now I don't remember how. I will attempt to solve this one later.
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.