Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Mock AIME 6 2006-2007 Problems/Problem 9"
Line 3: Line 3:
  
 
==Solution==
 
==Solution==
 +
[[File:MockAIME_6_P9.png|600px]]
  
−
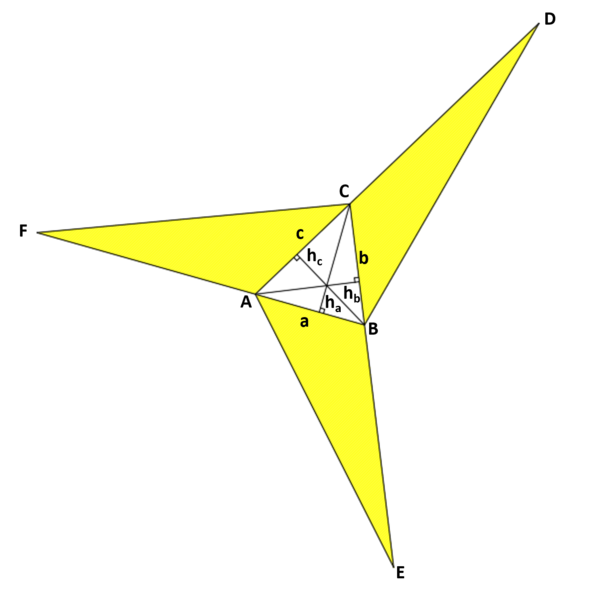
Let "a", "b", and "c", be the lengths of sides <math>AB</math>, <math>BC</math> and <math>CA</math> respectively.
+
Let <math>a</math>, <math>b</math>, and <math>c</math>, be the lengths of sides <math>AB</math>, <math>BC</math> and <math>CA</math> respectively.
  
−
Let "h_a", "h_b", and "h_c", be the heights of <math>\Delta ABC</math> from sides <math>AB</math>, <math>BC</math> and <math>CA</math> respectively.
+
Let <math>h_a</math>, <math>h_b</math>, and <math>h_c</math>, be the heights of <math>\Delta ABC</math> from sides <math>AB</math>, <math>BC</math> and <math>CA</math> respectively.
  
 
Since the areas of triangles <math>CBD</math>, <math>BAE</math>, and <math>ACF</math> are equal, then,
 
Since the areas of triangles <math>CBD</math>, <math>BAE</math>, and <math>ACF</math> are equal, then,
Line 24: Line 25:
 
<math>b=\frac{h_a}{h_b}a=\frac{14}{13}a</math> and <math>c=\frac{h_a}{h_c}a=\frac{15}{13}a</math>  
 
<math>b=\frac{h_a}{h_b}a=\frac{14}{13}a</math> and <math>c=\frac{h_a}{h_c}a=\frac{15}{13}a</math>  
  
−
Since "a", "b", and "c", and <math>13</math> is a prime number, then the minimum integer value that <math>a</math> can have in order for <math>b</math> and <math>c</math> to also be integer is <math>13</math>
+
Since <math>a</math>, <math>b</math>, and <math>c</math>, are integers, and <math>13</math> is a prime number, then the minimum integer value that <math>a</math> can have in order for <math>b</math> and <math>c</math> to also be integer is <math>13</math>
  
 
Therefore <math>a=13</math>, <math>b=14</math>, and <math>c=15</math>
 
Therefore <math>a=13</math>, <math>b=14</math>, and <math>c=15</math>

Revision as of 12:46, 26 November 2023

Problem

$ABC$ is a triangle with integer side lengths. Extend $\overline{AC}$ beyond $C$ to point $D$ such that $CD=120$. Similarly, extend $\overline{CB}$ beyond $B$ to point $E$ such that $BE=112$ and $\overline{BA}$ beyond $A$ to point $F$ such that $AF=104$. If triangles $CBD$, $BAE$, and $ACF$ all have the same area, what is the minimum possible area of triangle $ABC$?

Solution

MockAIME 6 P9.png

Let $a$, $b$, and $c$, be the lengths of sides $AB$, $BC$ and $CA$ respectively.

Let $h_a$, $h_b$, and $h_c$, be the heights of $\Delta ABC$ from sides $AB$, $BC$ and $CA$ respectively.

Since the areas of triangles $CBD$, $BAE$, and $ACF$ are equal, then,

$104h_a=112h_b=120h_c$

Therefore,

$\frac{h_a}{h_b}=\frac{112}{104}=\frac{14}{13}$ and $\frac{h_a}{h_c}=\frac{120}{104}=\frac{15}{13}$

Since the area of $\Delta ABC$ is half any base times it's height, then:

$ah_a=bh_b=ch_c$

Therefore,

$b=\frac{h_a}{h_b}a=\frac{14}{13}a$ and $c=\frac{h_a}{h_c}a=\frac{15}{13}a$

Since $a$, $b$, and $c$, are integers, and $13$ is a prime number, then the minimum integer value that $a$ can have in order for $b$ and $c$ to also be integer is $13$

Therefore $a=13$, $b=14$, and $c=15$

minimum possible area of triangle $ABC$ using Heron's formula is $ABC$ is:

$A_{ABC}=\sqrt{s(s-a)(s-b)(s-c)}$, where $s=\frac{a+b+c}{2}$

$s=\frac{13+14+15}{2}=21$

$A_{ABC}=\sqrt{(21)(6)(7)(8)}=\sqrt{3^24^27^2}=(3)(7)(4)=\boxed{84}$

~Tomas Diaz. orders@tomasdiaz.com

Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Mock_AIME_6_2006-2007_Problems/Problem_9&oldid=205894"