Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1979 USAMO Problems/Problem 2"

(→‎Solution)
 
(36 intermediate revisions by the same user not shown)
Line 3: Line 3:
 
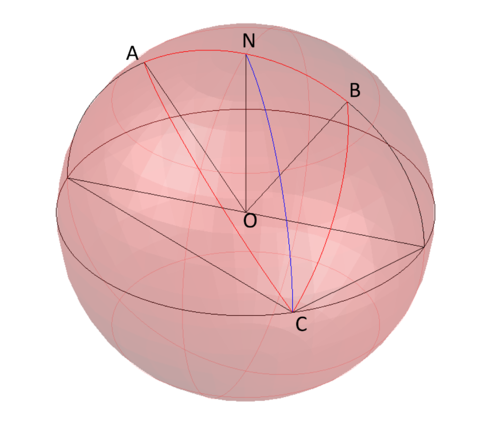
<math>N</math> is the north pole. <math>A</math> and <math>B</math> are points on a great circle through <math>N</math> equidistant from <math>N</math>. <math>C</math> is a point on the equator. Show that the great circle through <math>C</math> and <math>N</math> bisects the angle <math>ACB</math> in the spherical triangle <math>ABC</math> (a spherical triangle has great circle arcs as sides).
 
<math>N</math> is the north pole. <math>A</math> and <math>B</math> are points on a great circle through <math>N</math> equidistant from <math>N</math>. <math>C</math> is a point on the equator. Show that the great circle through <math>C</math> and <math>N</math> bisects the angle <math>ACB</math> in the spherical triangle <math>ABC</math> (a spherical triangle has great circle arcs as sides).
  
−
==Hint==
+
==Solution==
−
Draw a large diagram. A nice, large, and precise diagram. Note that drawing a sphere entails drawing a circle and then a dashed circle (preferably of a different color) perpendicular (in the plane) to the original circle.
+
 
 +
[[File:USAMO_1979_P2a.png|500px]]
  
−
==Solution==
 
 
Since <math>N</math> is the north pole, we define the Earth with a sphere of radius one in space with <math>N=(0,0,1)</math> and sphere center <math>O=(0,0,0)</math>
 
Since <math>N</math> is the north pole, we define the Earth with a sphere of radius one in space with <math>N=(0,0,1)</math> and sphere center <math>O=(0,0,0)</math>
−
We then pick point <math>N</math> on the sphere and define the <math>xz-plane</math> as the plane that contains great circle points <math>A</math> , <math>B</math>, and <math>N</math> with the <math>x-axis</math> perpendicular to the <math>z-axis</math> and in the direction of <math>A</math>.
+
We then pick point <math>N</math> on the sphere and define the <math>xz</math>-plane as the plane that contains great circle points <math>A</math> , <math>B</math>, and <math>N</math> with the <math>x</math>-axis perpendicular to the <math>z</math>-axis and in the direction of <math>A</math>.
  
−
Using this coordinate system and <math>x</math>, <math>y</math>, and <math>z</math> axes <math>A=(cos(\phi),0,sin(\phi))</math> where <math>\phi</math> is the angle from the <math>xy-plane</math> to <math>A</math> or latitude on this sphere with <math>\frac{-\pi}{2} < \phi < \frac{\pi}{2}</math>
+
Using this coordinate system and <math>x</math>, <math>y</math>, and <math>z</math> axes <math>A=(cos(\phi),0,sin(\phi))</math> where <math>\phi</math> is the angle from the <math>xy</math>-plane to <math>A</math> or latitude on this sphere with <math>\frac{-\pi}{2} < \phi < \frac{\pi}{2}</math>
  
 
Since <math>A</math> and <math>B</math> are points on a great circle through <math>N</math> equidistant from <math>N</math>, then <math>B=(-cos(\phi),0,sin(\phi))</math>  
 
Since <math>A</math> and <math>B</math> are points on a great circle through <math>N</math> equidistant from <math>N</math>, then <math>B=(-cos(\phi),0,sin(\phi))</math>  
  
−
Since <math>C</math> is a point on the equator, then <math>C=(cos(\theta),sin(\theta),0)</math> where <math>\theta</math> is the angle on the <math>xy-plane</math> from the origin to <math>C</math> or longitude on this sphere with <math>-\pi < \phi \le \pi</math>
+
Since <math>C</math> is a point on the equator, then <math>C=(cos(\theta),sin(\theta),0)</math> where <math>\theta</math> is the angle on the <math>xy</math>-plane from the origin to <math>C</math> or longitude on this sphere with <math>-\pi < \phi \le \pi</math>
  
 
We note that vectors from the origin to points <math>N</math>, <math>A</math>, <math>B</math>, and <math>C</math> are all unit vectors because all those points are on the unit sphere.
 
We note that vectors from the origin to points <math>N</math>, <math>A</math>, <math>B</math>, and <math>C</math> are all unit vectors because all those points are on the unit sphere.
Line 32: Line 32:
 
<math>\overrightarrow{V_{CN}}=(\overrightarrow{C}\times\overrightarrow{N})\times\overrightarrow{C}</math>
 
<math>\overrightarrow{V_{CN}}=(\overrightarrow{C}\times\overrightarrow{N})\times\overrightarrow{C}</math>
  
−
<math>\overrightarrow{V_{CN}}=(\overrightarrow{C}\times\overrightarrow{N})\times\overrightarrow{C}</math>
+
<math>\overrightarrow{V_{CN}}=(\left\langle cos(\theta),sin(\theta),0 \right\rangle\times\left\langle 0,0,1 \right\rangle)\times \left\langle cos(\theta),sin(\theta),0 \right\rangle</math>
−
<math>\left\langle \right\rangle</math>
+
 
 +
<math>\overrightarrow{V_{CN}}=\left\langle sin(\theta),-cos(\theta),0 \right\rangle\times \left\langle cos(\theta),sin(\theta),0 \right\rangle</math>
 +
 
 +
<math>\overrightarrow{V_{CN}}=\left\langle 0,0,sin^{2}(\theta)+cos^{2}(\theta) \right\rangle</math>
 +
 
 +
<math>\overrightarrow{V_{CN}}=\left\langle 0,0,1 \right\rangle</math>
 +
 
 +
Vector <math>\overrightarrow{V_{CA}}</math>:
 +
 
 +
<math>\overrightarrow{V_{CA}}=(\overrightarrow{C}\times\overrightarrow{A})\times\overrightarrow{C}</math>
 +
 
 +
<math>\overrightarrow{V_{CA}}=(\left\langle cos(\theta),sin(\theta),0 \right\rangle\times\left\langle cos(\phi),0,sin(\phi) \right\rangle)\times \left\langle cos(\theta),sin(\theta),0 \right\rangle</math>
 +
 
 +
<math>\overrightarrow{V_{CA}}=\left\langle sin(\theta)sin(\phi),-cos(\theta)sin(\phi),-sin(\theta)cos(\phi) \right\rangle\times \left\langle cos(\theta),sin(\theta),0 \right\rangle</math>
 +
 
 +
Since we're only interested in the <math>z</math> component of the vector
 +
 
 +
<math>\overrightarrow{V_{CA}}=\left\langle V_{CA_{x}},V_{CA_{y}},sin^{2}(\theta)sin(\phi)+cos^{2}(\theta)sin(\phi) \right\rangle</math>
 +
 
 +
<math>\overrightarrow{V_{CA}}=\left\langle V_{CA_{x}},V_{CA_{y}},sin(\phi) \right\rangle</math>
 +
 
 +
Vector <math>\overrightarrow{V_{CB}}</math>:
 +
 
 +
<math>\overrightarrow{V_{CB}}=(\overrightarrow{C}\times\overrightarrow{b})\times\overrightarrow{C}</math>
 +
 
 +
<math>\overrightarrow{V_{CB}}=(\left\langle cos(\theta),sin(\theta),0 \right\rangle\times\left\langle -cos(\phi),0,sin(\phi) \right\rangle)\times \left\langle cos(\theta),sin(\theta),0 \right\rangle</math>
 +
 
 +
<math>\overrightarrow{V_{CB}}=\left\langle sin(\theta)sin(\phi),-cos(\theta)sin(\phi),sin(\theta)cos(\phi) \right\rangle\times \left\langle cos(\theta),sin(\theta),0 \right\rangle</math>
 +
 
 +
Since we're only interested in the <math>z</math> component of the vector
 +
 
 +
<math>\overrightarrow{V_{CB}}=\left\langle V_{CB_{x}},V_{CB_{y}},sin^{2}(\theta)sin(\phi)+cos^{2}(\theta)sin(\phi) \right\rangle</math>
 +
 
 +
<math>\overrightarrow{V_{CB}}=\left\langle V_{CB_{x}},V_{CB_{y}},sin(\phi) \right\rangle</math>
 +
 
 +
Since we're working with unit vectors, then we can use dot products on the vectors with their angles as follows:
 +
 
 +
<math>cos(\angle ACN) = \overrightarrow{V_{CA}}\cdot \overrightarrow{V_{CN}}</math>
 +
 
 +
<math>cos(\angle ACN) = \left\langle V_{CA_{x}},V_{CA_{y}},sin(\phi) \right\rangle \cdot \left\langle 0,0,1 \right\rangle = 0*V_{CA_{x}}+0*V_{CA_{y}}+1*sin(\phi)=sin(\phi) </math>
 +
 
 +
Likewise,
 +
 
 +
<math>cos(\angle BCN) = \overrightarrow{V_{CB}}\cdot \overrightarrow{V_{CN}}</math>
 +
 
 +
<math>cos(\angle BCN) = \left\langle V_{CB_{x}},V_{CB_{y}},sin(\phi) \right\rangle \cdot \left\langle 0,0,1 \right\rangle = 0*V_{CB_{x}}+0*V_{CB_{y}}+1*sin(\phi)=sin(\phi) </math>
 +
 
 +
Therefore,
 +
 
 +
<math>cos(\angle ACN) = cos(\angle BCN)</math> and thus <math>\angle ACN = \angle BCN</math>
 +
 
 +
Since those angles are equal, it proves that the great circle through <math>C</math> and <math>N</math> bisects the <math>\angle ACB</math> in the spherical triangle <math>ABC</math>  
  
−
~Tomas Diaz
+
~Tomas Diaz.  orders@tomasdiaz.com
  
 
{{alternate solutions}}
 
{{alternate solutions}}

Latest revision as of 21:09, 21 November 2023

Problem

$N$ is the north pole. $A$ and $B$ are points on a great circle through $N$ equidistant from $N$. $C$ is a point on the equator. Show that the great circle through $C$ and $N$ bisects the angle $ACB$ in the spherical triangle $ABC$ (a spherical triangle has great circle arcs as sides).

Solution

USAMO 1979 P2a.png

Since $N$ is the north pole, we define the Earth with a sphere of radius one in space with $N=(0,0,1)$ and sphere center $O=(0,0,0)$ We then pick point $N$ on the sphere and define the $xz$-plane as the plane that contains great circle points $A$ , $B$, and $N$ with the $x$-axis perpendicular to the $z$-axis and in the direction of $A$.

Using this coordinate system and $x$, $y$, and $z$ axes $A=(cos(\phi),0,sin(\phi))$ where $\phi$ is the angle from the $xy$-plane to $A$ or latitude on this sphere with $\frac{-\pi}{2} < \phi < \frac{\pi}{2}$

Since $A$ and $B$ are points on a great circle through $N$ equidistant from $N$, then $B=(-cos(\phi),0,sin(\phi))$

Since $C$ is a point on the equator, then $C=(cos(\theta),sin(\theta),0)$ where $\theta$ is the angle on the $xy$-plane from the origin to $C$ or longitude on this sphere with $-\pi < \phi \le \pi$

We note that vectors from the origin to points $N$, $A$, $B$, and $C$ are all unit vectors because all those points are on the unit sphere.

So, we're going to define points $N$, $A$, $B$, and $C$ as unit vectors with their coordinates.

We also define the following vectors as follows:

Vector $\overrightarrow{V_{CN}}$ is the unit vector in the direction of arc $CN$ and tangent to the great circle of $CN$ at $C$

Vector $\overrightarrow{V_{CA}}$ is the unit vector in the direction of arc $CA$ and tangent to the great circle of $CA$ at $C$

Vector $\overrightarrow{V_{CB}}$ is the unit vector in the direction of arc $CB$ and tangent to the great circle of $CB$ at $C$

To calculate each of these vectors we shall use the cross product as follows:

$\overrightarrow{V_{CN}}=(\overrightarrow{C}\times\overrightarrow{N})\times\overrightarrow{C}$

$\overrightarrow{V_{CN}}=(\left\langle cos(\theta),sin(\theta),0 \right\rangle\times\left\langle 0,0,1 \right\rangle)\times \left\langle cos(\theta),sin(\theta),0 \right\rangle$

$\overrightarrow{V_{CN}}=\left\langle sin(\theta),-cos(\theta),0 \right\rangle\times \left\langle cos(\theta),sin(\theta),0 \right\rangle$

$\overrightarrow{V_{CN}}=\left\langle 0,0,sin^{2}(\theta)+cos^{2}(\theta) \right\rangle$

$\overrightarrow{V_{CN}}=\left\langle 0,0,1 \right\rangle$

Vector $\overrightarrow{V_{CA}}$:

$\overrightarrow{V_{CA}}=(\overrightarrow{C}\times\overrightarrow{A})\times\overrightarrow{C}$

$\overrightarrow{V_{CA}}=(\left\langle cos(\theta),sin(\theta),0 \right\rangle\times\left\langle cos(\phi),0,sin(\phi) \right\rangle)\times \left\langle cos(\theta),sin(\theta),0 \right\rangle$

$\overrightarrow{V_{CA}}=\left\langle sin(\theta)sin(\phi),-cos(\theta)sin(\phi),-sin(\theta)cos(\phi) \right\rangle\times \left\langle cos(\theta),sin(\theta),0 \right\rangle$

Since we're only interested in the $z$ component of the vector

$\overrightarrow{V_{CA}}=\left\langle V_{CA_{x}},V_{CA_{y}},sin^{2}(\theta)sin(\phi)+cos^{2}(\theta)sin(\phi) \right\rangle$

$\overrightarrow{V_{CA}}=\left\langle V_{CA_{x}},V_{CA_{y}},sin(\phi) \right\rangle$

Vector $\overrightarrow{V_{CB}}$:

$\overrightarrow{V_{CB}}=(\overrightarrow{C}\times\overrightarrow{b})\times\overrightarrow{C}$

$\overrightarrow{V_{CB}}=(\left\langle cos(\theta),sin(\theta),0 \right\rangle\times\left\langle -cos(\phi),0,sin(\phi) \right\rangle)\times \left\langle cos(\theta),sin(\theta),0 \right\rangle$

$\overrightarrow{V_{CB}}=\left\langle sin(\theta)sin(\phi),-cos(\theta)sin(\phi),sin(\theta)cos(\phi) \right\rangle\times \left\langle cos(\theta),sin(\theta),0 \right\rangle$

Since we're only interested in the $z$ component of the vector

$\overrightarrow{V_{CB}}=\left\langle V_{CB_{x}},V_{CB_{y}},sin^{2}(\theta)sin(\phi)+cos^{2}(\theta)sin(\phi) \right\rangle$

$\overrightarrow{V_{CB}}=\left\langle V_{CB_{x}},V_{CB_{y}},sin(\phi) \right\rangle$

Since we're working with unit vectors, then we can use dot products on the vectors with their angles as follows:

$cos(\angle ACN) = \overrightarrow{V_{CA}}\cdot \overrightarrow{V_{CN}}$

$cos(\angle ACN) = \left\langle V_{CA_{x}},V_{CA_{y}},sin(\phi) \right\rangle \cdot \left\langle 0,0,1 \right\rangle = 0*V_{CA_{x}}+0*V_{CA_{y}}+1*sin(\phi)=sin(\phi)$

Likewise,

$cos(\angle BCN) = \overrightarrow{V_{CB}}\cdot \overrightarrow{V_{CN}}$

$cos(\angle BCN) = \left\langle V_{CB_{x}},V_{CB_{y}},sin(\phi) \right\rangle \cdot \left\langle 0,0,1 \right\rangle = 0*V_{CB_{x}}+0*V_{CB_{y}}+1*sin(\phi)=sin(\phi)$

Therefore,

$cos(\angle ACN) = cos(\angle BCN)$ and thus $\angle ACN = \angle BCN$

Since those angles are equal, it proves that the great circle through $C$ and $N$ bisects the $\angle ACB$ in the spherical triangle $ABC$

~Tomas Diaz. orders@tomasdiaz.com

Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.

See Also

1979 USAMO (Problems • Resources)
Preceded by
Problem 1 		Followed by
Problem 3
1 • 2 • 3 • 4 • 5
All USAMO Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1979_USAMO_Problems/Problem_2&oldid=205195"