Difference between revisions of "2023 AMC 12B Problems/Problem 17"

Revision as of 22:18, 15 November 2023

Problem

Triangle ABC has side lengths in arithmetic progression, and the smallest side has length $6.$ If the triangle has an angle of $120^\circ,$ what is the area of $ABC$ ?

$\textbf{(A) }12\sqrt{3}\qquad\textbf{(B) }8\sqrt{6}\qquad\textbf{(C) }14\sqrt{2}\qquad\textbf{(D) }20\sqrt{2}\qquad\textbf{(E) }15\sqrt{3}$

Solution 1

The length of the side opposite to the angle with $120^\circ$ is longest. We denote its value as $x$ .

Because three side lengths form an arithmetic sequence, the middle-valued side length is $\frac{x + 6}{2}$ .

Following from the law of cosines, we have $\begin{align*} 6^2 + \left( \frac{x + 6}{2} \right)^2 - 2 \cdot 6 \cdot \frac{x + 6}{2} \cdot \cos 120^\circ = x^2 . \end{align*}$

By solving this equation, we get $x = 14$ . Thus, $\frac{x + 6}{2} = 10$ .

Therefore, the area of the triangle is $\begin{align*} \frac{1}{2} 6 \cdot 10 \cdot \sin 120^\circ = \boxed{\textbf{(E) } 15 \sqrt{3}} . \end{align*}$

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Solution 2 (Analytic Geometry)

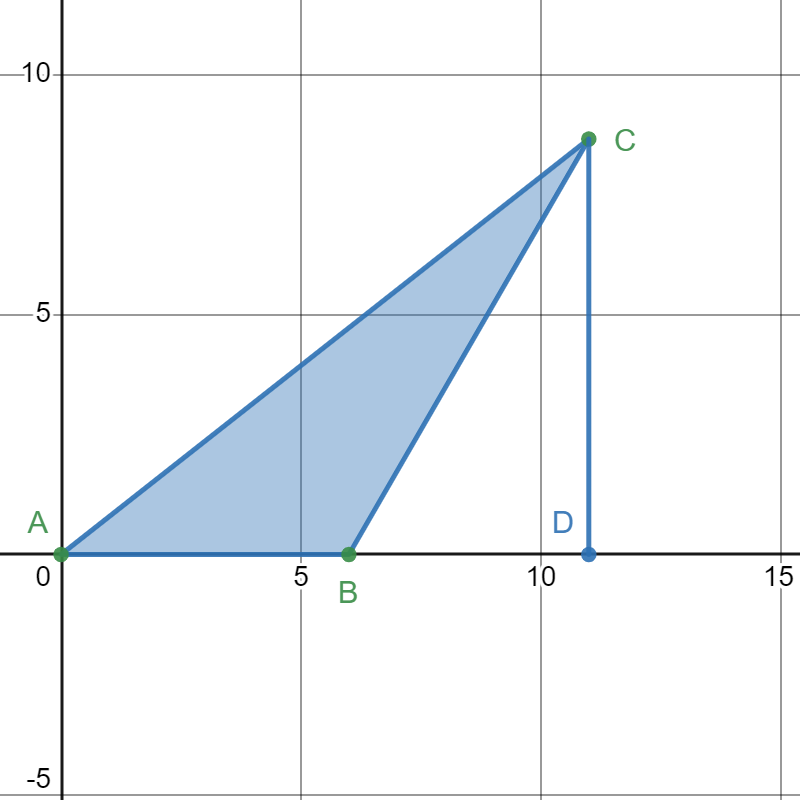
Since the triangle's longest side must correspond to the $120^\circ$ angle, the triangle is unique. By analytic geometry, we construct the following plot.

We know the coordinates of point $A$ being the origin and $B$ being $(6,0)$ . Constructing the line which point $C$ can lay on, here since $\angle B=120^\circ$ , $C$ is on the line $y=\sqrt{3}\left(x-6\right).$

I denote $D$ as the perpendicular line from $C$ to $AB$ , and assume $CD=k$ . Here we know $\triangle BCD$ is a $30^\circ-60^\circ-90-^\circ$ triangle. Hence $DC=\sqrt{3}k$ and $BC=2k$ .

Furthermore, due to the arithmetic progression, we know $AC=4k-6$ . Hence, in $\triangle ACD$ , $\left(4k-6\right)^{2}=\left(6+k\right)^{2}+3k^{2},$ $k=5.$

Thus, the area is equal to $\frac{1}{2}\cdot 6\cdot \sqrt{3} k=15\sqrt{3}$ .

- Prof. Joker

Solution 3

Let the side lengths be $6$ , $6+d$ , and $6+2d$ . As $6+2d$ is the longest side, the angle opposite to it will be $120^{\circ}$ .

By the law of Cosine $(6+2d)^2 = 6^2 + (6+d)^2 - 2 \cdot 6 \cdot (6+d) \cdot \cos 120^{\circ}$ $4d^2 + 24d + 36 = 36 + 36 + 12 d + d^2 + 36 + 6d$ $3d^2 + 6d - 72 = 0$ $d^2 + 2d - 24 = 0$ $(d+6)(d-4)=0$

As $d>0$ , $d = 4$ , $6+d = 10$

Therefore, $[ABC] = \frac{ 6 \cdot 10 \cdot \sin 120^{\circ} }{2} = \boxed{\textbf{(E) } 15 \sqrt{3}}$

~isabelchen

@@ Line 33: / Line 33: @@
 ~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
-==Solution 2==
+==Solution 2 (Analytic Geometry)==
-Let the side lengths be <math>6</math>, <math>x</math>, and <math>2x-6</math>. As <math>2x-6</math> is the longest side, the angle opposite to it will be <math>120^{\circ}</math>.
+Since the triangle's longest side must correspond to the <math>120^\circ</math> angle, the triangle is unique. By analytic geometry, we construct the following plot.
+[[File:PJ_2023_12B_Q17.png]]
-By the law of Cosine
+We know the coordinates of point <math>A</math> being the origin and <math>B</math> being <math>(6,0)</math>. Constructing the line which point <math>C</math> can lay on, here since <math>\angle B=120^\circ</math>, <math>C</math> is on the line <cmath>y=\sqrt{3}\left(x-6\right).</cmath>
-<cmath>(2x-6)^2 = 6^2 + x^2 - 2 \cdot 6 \cdot x \cdot \cos 120^{\circ}</cmath>
-<cmath>4x^2 - 24x + 36 = 36 + x^2 + 6x</cmath>
+I denote <math>D</math> as the perpendicular line from <math>C</math> to <math>AB</math>, and assume <math>CD=k</math>. Here we know <math>\triangle BCD</math> is a <math>30^\circ-60^\circ-90-^\circ</math> triangle. Hence <math>DC=\sqrt{3}k</math> and <math>BC=2k</math>.
-<cmath>3x^2 - 30x = 0</cmath>
-<cmath>x^2 - 10x = 0</cmath>
-As <math>x \neq 0</math>, <math>x = 10</math>.
+Furthermore, due to the arithmetic progression, we know <math>AC=4k-6</math>. Hence, in <math>\triangle ACD</math>, <cmath>\left(4k-6\right)^{2}=\left(6+k\right)^{2}+3k^{2},</cmath> <cmath>k=5.</cmath>
-Therefore, <math>[ABC] = \frac{ 6 \cdot 10 \cdot \sin 120^{\circ} }{2} = \boxed{\textbf{(E) } 15 \sqrt{3}} </math>
+Thus, the area is equal to <math>\frac{1}{2}\cdot 6\cdot \sqrt{3} k=15\sqrt{3}</math>.
-~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
+- Prof. Joker
 ==Solution 3==
@@ Line 65: / Line 65: @@
 ~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
-==Solution 4 (Analytic Geometry)==
-Since the triangle's longest side must correspond to the <math>120^\circ</math> angle, the triangle is unique. By analytic geometry, we construct the following plot.
-[[File:PJ_2023_12B_Q17.png]]
-We know the coordinates of point <math>A</math> being the origin and <math>B</math> being <math>(6,0)</math>. Constructing the line which point <math>C</math> can lay on, here since <math>\angle B=120^\circ</math>, <math>C</math> is on the line <cmath>y=\sqrt{3}\left(x-6\right).</cmath>
-I denote <math>D</math> as the perpendicular line from <math>C</math> to <math>AB</math>, and assume <math>CD=k</math>. Here we know <math>\triangle BCD</math> is a <math>30^\circ-60^\circ-90-^\circ</math> triangle. Hence <math>DC=\sqrt{3}k</math> and <math>BC=2k</math>.
-Furthermore, due to the arithmetic progression, we know <math>AC=4k-6</math>. Hence, in <math>\triangle ACD</math>, <cmath>\left(4k-6\right)^{2}=\left(6+k\right)^{2}+3k^{2},</cmath> <cmath>k=5.</cmath>
-Thus, the area is equal to <math>\frac{1}{2}\cdot 6\cdot \sqrt{3} k=15\sqrt{3}</math>.
-- Prof. Joker
 ==See Also==
 {{AMC12 box|year=2023|ab=B|num-b=16|num-a=18}}
 {{MAA Notice}}

2023 AMC 12B (Problems • Answer Key • Resources)
Preceded by Problem 16	Followed by Problem 18
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search