Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Symmetry"

(Created page with "A proof utilizes '''symmetry''' if the steps to prove one thing is identical to those steps of another. For example, to prove that in triangle ABC with all three sides congruent ...")
 
Line 1: Line 1:
−
A proof utilizes '''symmetry''' if the steps to prove one thing is identical to those steps of another. For example, to prove that in triangle ABC with all three sides congruent to each other that all three angles are equal, you only need to prove that if AB = AC, then <C = <B; the other cases hold by symmetry because the steps are the same.
+
A proof utilizes '''symmetry''' if the steps to prove one thing is identical to those steps of another. For example, to prove that in triangle ABC with all three sides congruent to each other that all three angles are equal, you only need to prove that if <math>AB = AC,</math> then <math>\angle C = \angle B;</math> the other cases hold by symmetry because the steps are the same.
 +
==Hidden symmetry==
 +
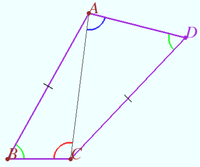
[[File:Hidden S.png|200px|right]]
 +
Let the convex quadrilateral <math>ABCD</math> be given.
 +
<cmath>AC = DE, \angle CAD + \angle ACB = 180^\circ.</cmath>
 +
 
 +
Prove that <math>\angle ABC = \angle ADC.</math>
 +
 +
<i><b>Proof</b></i>
 +
 
 +
Let <math>\ell</math> be bisector <math>AC.</math>
 +
 
 +
Let point <math>E</math> be symmetric <math>D</math> with respect  <math>\ell.</math>
 +
 
 +
<cmath>\angle CAD = \angle ACE \implies \angle CAD + \angle ACB = 180^\circ \implies E \in BC.</cmath>
 +
<math>AE = CD = AB \implies \triangle ABE</math> is isosceles.
 +
 
 +
Therefore <math>\angle ABC = \angle AEC = \angle ADC \blacksquare.</math>

Revision as of 13:34, 28 August 2023

A proof utilizes symmetry if the steps to prove one thing is identical to those steps of another. For example, to prove that in triangle ABC with all three sides congruent to each other that all three angles are equal, you only need to prove that if $AB = AC,$ then $\angle C = \angle B;$ the other cases hold by symmetry because the steps are the same.

Hidden symmetry

Hidden S.png

Let the convex quadrilateral $ABCD$ be given. \[AC = DE, \angle CAD + \angle ACB = 180^\circ.\]

Prove that $\angle ABC = \angle ADC.$

Proof

Let $\ell$ be bisector $AC.$

Let point $E$ be symmetric $D$ with respect $\ell.$

\[\angle CAD = \angle ACE \implies \angle CAD + \angle ACB = 180^\circ \implies E \in BC.\] $AE = CD = AB \implies \triangle ABE$ is isosceles.

Therefore $\angle ABC = \angle AEC = \angle ADC \blacksquare.$

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Symmetry&oldid=197573"