Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2002 AMC 12B Problems/Problem 20"

m (→‎Solution)
(→‎Video Solution by OmegaLearn)
 
(10 intermediate revisions by 4 users not shown)
Line 1: Line 1:
 
{{duplicate|[[2002 AMC 12B Problems|2002 AMC 12B #20]] and [[2002 AMC 10B Problems|2002 AMC 10B #22]]}}
 
{{duplicate|[[2002 AMC 12B Problems|2002 AMC 12B #20]] and [[2002 AMC 10B Problems|2002 AMC 10B #22]]}}
 
== Problem ==
 
== Problem ==
−
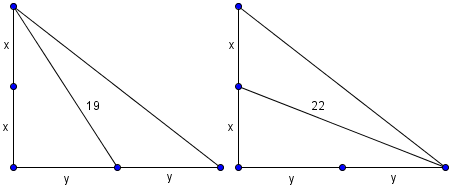
Let <math>\triangle XOY</math> be a [[right triangle|right-angled triangle]] with <math>m\angle XOY = 90^{\circ}</math>. Let <math>M</math> and <math>N</math> be the [[midpoint]]s of legs <math>OX</math> and <math>OY</math>, respectively. Given that <math>XN = 19</math> and <math>YM = 22</math>, find <math>XY</math>.
+
Let <math>\triangle XOY</math> be a [[right triangle|right-angled triangle]] with <math>m\angle XOY = 90^{\circ}</math>. Let <math>M</math> and <math>N</math> be the [[midpoint]]s of legs <math>OX</math> and <math>OY</math>, respectively. Given that <math>XN = 19</math> and <math>YM = 22</math>, find <math>XY</math>.  
  
 
<math>\mathrm{(A)}\ 24
 
<math>\mathrm{(A)}\ 24
Line 8: Line 8:
 
\qquad\mathrm{(D)}\ 30
 
\qquad\mathrm{(D)}\ 30
 
\qquad\mathrm{(E)}\ 32</math>
 
\qquad\mathrm{(E)}\ 32</math>
−
== Solution ==
+
 
 +
== Solution 1 ==  
 
[[Image:2002_12B_AMC-20.png]]
 
[[Image:2002_12B_AMC-20.png]]
  
Line 24: Line 25:
  
 
Alternatively, we could note that since we found <math>x^2 + y^2 = 169</math>, segment <math>MN=13</math>. Right triangles <math>\triangle MON</math> and <math>\triangle XOY</math> are similar by Leg-Leg with a ratio of <math>\frac{1}{2}</math>, so <math>XY=2(MN)=\boxed{\mathrm{(B)}\ 26}</math>
 
Alternatively, we could note that since we found <math>x^2 + y^2 = 169</math>, segment <math>MN=13</math>. Right triangles <math>\triangle MON</math> and <math>\triangle XOY</math> are similar by Leg-Leg with a ratio of <math>\frac{1}{2}</math>, so <math>XY=2(MN)=\boxed{\mathrm{(B)}\ 26}</math>
 +
 +
 +
== Solution 2 ==
 +
Let <math>XO=x</math> and <math>YO=y.</math> Then, <math>XY=\sqrt{x^2+y^2}.</math>
 +
 +
Since <math>XN=19</math> and <math>YM=22,</math>
 +
<cmath>XN^2=19^2=x^2+(\dfrac{y}{2})^2)=\dfrac{x^2}{4}+y^2</cmath>
 +
<cmath>YM^2=22^2=(\dfrac{x}{2})^2+y^2=\dfrac{x^2}{4}+y^2.</cmath>
 +
 +
Adding these up:
 +
<cmath>19^2+22^2=\dfrac{4x^2+y^2}{4}+\dfrac{x^2+4y^2}{4}</cmath>
 +
<cmath>845=\dfrac{5x^2+5y^2}{4}</cmath>
 +
<cmath>3380=5x^2+5y^2</cmath>
 +
<cmath>676=x^2+y^2.</cmath>
 +
 +
Then, we substitute: <math>XY=\sqrt{x^2+y^2}=\sqrt{676}=\boxed{26}.</math>
 +
 +
 +
== Solution 3 (Solution 1 but shorter) ==
 +
Refer to the diagram in solution 1. <math>4x^2+y^2=361</math> and <math>4y^2+x^2=484</math>, so add them: <math>5x^2+5y^2=845</math> and divide by 5: <math>x^2+y^2=169</math> so <math>\dfrac{XY}{2}=\sqrt{169}=13</math> and so <math>XY=26</math>, or answer <math>B</math>.
 +
 +
== Solution 4 ==
 +
Use the diagram in solution 1. Get <math>4x^2+y^2=361</math> and <math>4y^2+x^2=484</math>, and multiply the second equation by 4 to get <math>4x^2+16y^2=1936</math> and then subtract the first from the second. Get <math>15y^2=1575</math> and <math>y^2=105</math>. Repeat for the other variable to get <math>15x^2=960</math> and <math>x^2=64</math>. Now XY is equal to the square root of four times these quantities, so <math>(105+64) \cdot 4=676</math>, and <math>XY=26</math>
 +
 +
 +
== Video Solution by OmegaLearn ==
 +
https://youtu.be/BIyhEjVp0iM?t=174
 +
 +
~ pi_is_3.14
 +
 +
== Video Solution ==
 +
https://www.youtube.com/watch?v=7wj6RupkO90  ~David
  
 
== See also ==
 
== See also ==

Latest revision as of 14:02, 17 August 2023

The following problem is from both the 2002 AMC 12B #20 and 2002 AMC 10B #22, so both problems redirect to this page.

Problem

Let $\triangle XOY$ be a right-angled triangle with $m\angle XOY = 90^{\circ}$. Let $M$ and $N$ be the midpoints of legs $OX$ and $OY$, respectively. Given that $XN = 19$ and $YM = 22$, find $XY$.

$\mathrm{(A)}\ 24 \qquad\mathrm{(B)}\ 26 \qquad\mathrm{(C)}\ 28 \qquad\mathrm{(D)}\ 30 \qquad\mathrm{(E)}\ 32$

Solution 1

2002 12B AMC-20.png

Let $OM = x$, $ON = y$. By the Pythagorean Theorem on $\triangle XON, MOY$ respectively, \begin{align*} (2x)^2 + y^2 &= 19^2\\ x^2 + (2y)^2 &= 22^2\end{align*}

Summing these gives $5x^2 + 5y^2 = 845 \Longrightarrow x^2 + y^2 = 169$.

By the Pythagorean Theorem again, we have

\[(2x)^2 + (2y)^2 = XY^2 \Longrightarrow XY = \sqrt{4(x^2 + y^2)} = \sqrt{4(169)} = \sqrt{676} = \boxed{\mathrm{(B)}\ 26}\]

Alternatively, we could note that since we found $x^2 + y^2 = 169$, segment $MN=13$. Right triangles $\triangle MON$ and $\triangle XOY$ are similar by Leg-Leg with a ratio of $\frac{1}{2}$, so $XY=2(MN)=\boxed{\mathrm{(B)}\ 26}$


Solution 2

Let $XO=x$ and $YO=y.$ Then, $XY=\sqrt{x^2+y^2}.$

Since $XN=19$ and $YM=22,$ \[XN^2=19^2=x^2+(\dfrac{y}{2})^2)=\dfrac{x^2}{4}+y^2\] \[YM^2=22^2=(\dfrac{x}{2})^2+y^2=\dfrac{x^2}{4}+y^2.\]

Adding these up: \[19^2+22^2=\dfrac{4x^2+y^2}{4}+\dfrac{x^2+4y^2}{4}\] \[845=\dfrac{5x^2+5y^2}{4}\] \[3380=5x^2+5y^2\] \[676=x^2+y^2.\]

Then, we substitute: $XY=\sqrt{x^2+y^2}=\sqrt{676}=\boxed{26}.$


Solution 3 (Solution 1 but shorter)

Refer to the diagram in solution 1. $4x^2+y^2=361$ and $4y^2+x^2=484$, so add them: $5x^2+5y^2=845$ and divide by 5: $x^2+y^2=169$ so $\dfrac{XY}{2}=\sqrt{169}=13$ and so $XY=26$, or answer $B$.

Solution 4

Use the diagram in solution 1. Get $4x^2+y^2=361$ and $4y^2+x^2=484$, and multiply the second equation by 4 to get $4x^2+16y^2=1936$ and then subtract the first from the second. Get $15y^2=1575$ and $y^2=105$. Repeat for the other variable to get $15x^2=960$ and $x^2=64$. Now XY is equal to the square root of four times these quantities, so $(105+64) \cdot 4=676$, and $XY=26$


Video Solution by OmegaLearn

https://youtu.be/BIyhEjVp0iM?t=174

~ pi_is_3.14

Video Solution

https://www.youtube.com/watch?v=7wj6RupkO90 ~David

See also

2002 AMC 10B (Problems • Answer Key • Resources)
Preceded by
Problem 21 		Followed by
Problem 23
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions
2002 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 19 		Followed by
Problem 21
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2002_AMC_12B_Problems/Problem_20&oldid=197114"