Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Spieker center"

(Created page with "The Spieker center is defined as the center of mass of the perimeter of the triangle. The Spieker center of a <math>\triangle ABC</math> is the center of gravity of a homogene...")
 
(→‎Shatunov triangle)
 
(11 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
The Spieker center is defined as the center of mass of the perimeter of the triangle. The Spieker center of a <math>\triangle ABC</math> is the center of gravity of a homogeneous wire frame in the shape of <math>\triangle ABC.</math> The Spieker center is a triangle center and it is listed as the point <math>X_{10}.</math>
 
The Spieker center is defined as the center of mass of the perimeter of the triangle. The Spieker center of a <math>\triangle ABC</math> is the center of gravity of a homogeneous wire frame in the shape of <math>\triangle ABC.</math> The Spieker center is a triangle center and it is listed as the point <math>X_{10}.</math>
 +
 +
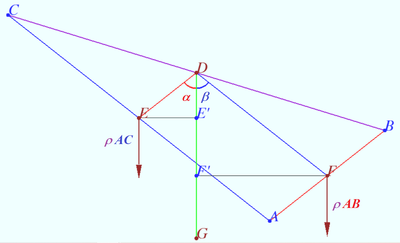
==Incenter of medial triangle==
 +
[[File:Physical proof.png|400px|right]]
 +
Prove that the Spieker center of triangle <math>\triangle ABC</math> is the incenter of the medial triangle <math>\triangle DEF</math> of a <math>\triangle ABC.</math>
 +
 +
<i><b>Proof</b></i>
 +
 +
Let's hang up the <math>\triangle ABC</math> in the middle of side <math>BC.</math> Side <math>BC</math> is balanced.
 +
 +
Let's replace side <math>AC</math> with point <math>E</math> (the center of mass of <math>AC,</math> the midpoint <math>AC).</math> Denote <math>\rho</math> the linear density of a homogeneous wire frame.
 +
 +
The mass of point <math>E</math> is equal to <math>\rho \cdot AC,</math> the shoulder of the gravity force is <math>EE' = ED \sin \alpha = \frac {AB \sin \alpha }{2}.</math>
 +
 +
The moment of this force is <math>g EE' \rho \cdot AC = \frac {g \rho\cdot AC \cdot AB}{2} \sin \alpha.</math>
 +
 +
Similarly the moment gravity force acting on AB is <math> \frac {g \rho\cdot AC \cdot AB}{2} \sin \beta.</math>
 +
 +
Therefore, equilibrium condition is <math>\alpha = \beta</math> and the center of gravity of a homogeneous wire frame  <math>ABC</math> lies on each bisector of <math>\triangle DEF.</math>
 +
 +
This point is the incenter of the medial triangle <math>\triangle DEF.</math>
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
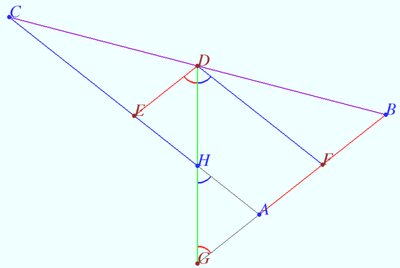
==Intersection of three cleavers==
 +
[[File:Cleaver.png|400px|right]]
 +
Prove that the Spieker center is located at the intersection of the three cleavers of triangle. A cleaver of a triangle is a line segment that bisects the perimeter of the triangle and has one endpoint at the midpoint of one of the three sides.
 +
 +
<i><b>Proof</b></i>
 +
 +
We use notation of previous proof. <math>DG</math> is the segment contains the Spieker center, <math>G \in AB, \angle EDG = \angle FDG, H = DG \cap AC.</math> WLOG, <math>AC > AB.</math>
 +
<cmath>DF||AC \implies \angle AHG = \angle FDG.</cmath>
 +
Similarly, <math> \angle AGH = \angle EDG =  \angle AHG.</math>
 +
 +
So <math>AH = AG \implies CH = AB + AH \implies DH</math> is cleaver.
 +
 +
Therefore, the three cleavers meet at the Spieker center.
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
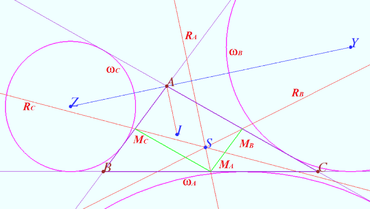
==Radical center of excircles==
 +
[[File:Radical center.png|370px|right]]
 +
Prove that the Spieker center of triangle is the radical center of the three excircles.
 +
 +
<i><b>Proof</b></i>
 +
 +
Let <math>\triangle ABC</math> be given,<math>M_A, M_B, M_C</math> be the midpoints of <math>BC, AC, BC,</math> respectively.
 +
 +
Let <math>\omega_A, \omega_B, \omega_C</math> be A-excircle, B-excircle, C-excircle centered at <math>X,Y,Z,</math> respectively.
 +
 +
Let <math>I</math> be the incenter of <math>\triangle ABC.</math>
 +
Let <math>R_A</math> be the radical axis of <math>\omega_B</math> and <math>\omega_C, R_B</math> be the radical axis of <math>\omega_A</math> and <math>\omega_C, R_C</math> be the radical axis of <math>\omega_B</math> and <math>\omega_A,</math> respectively.
 +
 +
It is known that the distances from <math>B</math> to the tangent points of <math>\omega_C</math> is equal to the distances from <math>C</math> to the tangent points of <math>\omega_B, BM_A = CM_A</math> therefore <math>M_A</math> lies on the radical axis <math>R_A</math> of <math>\omega_B</math> and <math>\omega_C.</math> Similarly, <math>M_B \in R_B, M_C \in R_C.</math>
 +
 +
<math>AI \perp ZY, R_A \perp XY \implies AI || RA \implies R_A</math> is cleaver. Similarly, <math>R_B</math> and <math>R_C</math> are cleavers.
 +
 +
Therefore the radical center of the three excircles coinside with the intersection of the three cleavers of triangle.
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
==Nagel line==
 +
[[File:Nagel line.png|400px|right]]
 +
Let points <math>I, G, S</math>  be the incenter, the centroid and the  Spieker center of triangle <math>\triangle ABC,</math> respectively. Prove that points <math>I, G, S</math> are collinear, <math>IG = 2 GS,</math> and the barycentric coordinates of S are  <math>{ b+c : c+a : a+b.}</math>
 +
 +
The Nagel line is the line on which points <math>I, G, S,</math> and Nagel point <math>N</math> lie.
 +
 +
<i><b>Proof</b></i>
 +
 +
Let <math>D, E, F</math> be the midpoints of <math>BC, AC, BC,</math> respectively.
 +
Bisector <math>AI</math> is parallel to cleaver <math>DS, BI || ES.</math>
 +
<cmath>AB ||ED, \frac {AB}{DE} = 2 \implies \triangle ABI \sim \triangle DES \implies \frac {AI}{DS} = 2.</cmath>
 +
Centroid <math>G</math> divide the median <math>AD</math> such that <math>\frac {AG}{DG} = 2 \implies </math>
 +
 +
<math>\triangle AGI \sim \triangle DGS \implies \frac {GI}{SG} = 2,</math> and points <math>I, G, S</math> are collinear.
 +
 +
The barycentric coordinates of <math>I</math> are <math>{a : b : c}.</math> The barycentric coordinates of <math>G</math> are <math>{1 : 1 : 1}.</math>
 +
 +
<cmath>\vec {GI} = 2 \vec {SG} \implies \vec {G} - \vec {I} = 2(\vec {S} - \vec {G}) \implies</cmath>
 +
<cmath>\vec {G} = \frac {3 \vec {G} - \vec {I} }{2} = {1 - \frac{a}{a+ b+c} : 1 - \frac {b}{a+b+c} : 1 - \frac{c}{a+b+c}} = { b+c : c+a : a+b.}</cmath>
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
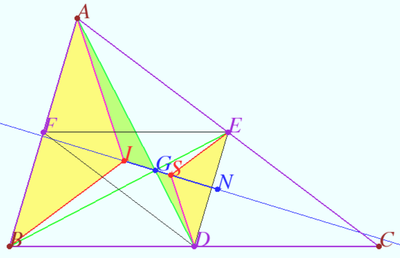
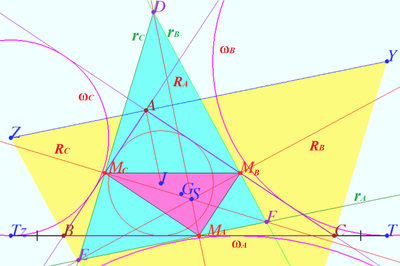
==Shatunov triangle==
 +
[[File:Shatunov triangle A.png|400px|right]]
 +
Let <math>\triangle ABC</math> be given. Let <math>\omega, \omega_A, \omega_B, \omega_C</math> be incircle, A-excircle, B-excircle, C-excircle centered at points <math>I,X,Y,Z,</math> respectively.
 +
 +
Let <math>r_A = EF, r_B = DF, r_C = DE</math> be  the radical axes of the inscribed circle and one of the excircles of <math>\triangle ABC.</math>
 +
 +
The triangle <math>\triangle DEF</math> whose sides are <math>r_A, r_B, r_C</math> we name the Shatunov triangle. Accordingly, the vertices of the Shatunov triangle are the radical centers of a pair of excircles and an inscribed circle.
 +
 +
Prove:
 +
 +
a) the heights of the Shatunov triangle lie on the bisectors of the medial triangle. The orthocenter of the Shatunov triangle is the Steiner point of <math>\triangle ABC.</math>
 +
 +
b) The Shatunov triangle is homothetic to the anticomplementary triangle of <math>\triangle ABC</math> with respect to the centroid <math>ABC</math> with coefficient <math>\frac {1}{2}.</math>
 +
 +
<i><b>Proof</b></i>
 +
 +
a) Let <math>M_A, M_B, M_C</math> be the midpoints of <math>BC, AC, AB,</math> respectively.
 +
 +
The distances from <math>M_A</math> to the tangent points of <math>\omega</math> and <math>\omega_A</math> are the same, so <math>M_A \in r_A.</math> Similarly <math>M_B \in r_B, M_C \in r_C.</math>
 +
 +
Let <math>T</math> and <math>T_Z</math> be the points of tangency of <math>BC</math> and <math>\omega_B</math> and <math>\omega_C,</math> respectively.
 +
 +
It is clear that <math>TC = BT_Z, BM_A = CM_A \implies M_A</math> lies on the radical axis <math>R_A.</math>
 +
 +
Similarly, <math>M_B</math> lies on the radical axis <math>R_B, M_C</math> lies on the radical axis <math>R_C.</math>
 +
 
 +
<math>D = r_B \cap r_C  \implies</math> D is the radical center of <math>\omega, \omega_B, \omega_C \implies D \in R_A \implies R_A = DM_A.</math>
 +
 +
<math>AI \perp ZY, R_A \perp ZY, r_A \perp AI \implies  DM_A \perp EF.</math> Similarly <math>EM_B \perp DF, FM_C \perp DE.</math>
 +
 +
Therefore <math>DM_A, EM_B, FM_C</math> are the heights of <math>\triangle DEF \implies S</math> is the orthocenter of <math>\triangle DEF.</math>
 +
 +
<math>\triangle M_AM_BM_C</math> is the medial triangle of <math>\triangle ABC, DSM_A</math>
 +
is the bisector of <math>\angle M_BM_AM_C \implies S</math> is the Steiner point of <math>\triangle ABC.</math>
 +
 +
b) <math>ZY || EF, XY || ED, ZX || FD \implies \triangle DEF \sim \triangle XYZ.</math>
 +
 +
<math>I</math> is the orthocenter of <math>\triangle XYZ, S</math> is the orthocenter of <math>\triangle DEF.</math>
 +
 +
Points <math>I, G,</math> and <math>S,</math> where <math>G</math> is the centroid <math>ABC,</math>  are collinear,  sides of is the <math>\triangle DEF</math> are parallel to the respective sides of <math>\triangle XYZ \implies \triangle DEF</math> is homothetic to the <math>\triangle XYZ</math> with respect to <math>G.</math>
 +
 +
<math>IG = 2CS \implies</math> the coefficient of homothety is <math>\frac {1}{2}.</math>
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''

Latest revision as of 05:48, 8 August 2023

The Spieker center is defined as the center of mass of the perimeter of the triangle. The Spieker center of a $\triangle ABC$ is the center of gravity of a homogeneous wire frame in the shape of $\triangle ABC.$ The Spieker center is a triangle center and it is listed as the point $X_{10}.$

Incenter of medial triangle

Physical proof.png

Prove that the Spieker center of triangle $\triangle ABC$ is the incenter of the medial triangle $\triangle DEF$ of a $\triangle ABC.$

Proof

Let's hang up the $\triangle ABC$ in the middle of side $BC.$ Side $BC$ is balanced.

Let's replace side $AC$ with point $E$ (the center of mass of $AC,$ the midpoint $AC).$ Denote $\rho$ the linear density of a homogeneous wire frame.

The mass of point $E$ is equal to $\rho \cdot AC,$ the shoulder of the gravity force is $EE' = ED \sin \alpha = \frac {AB \sin \alpha }{2}.$

The moment of this force is $g EE' \rho \cdot AC = \frac {g \rho\cdot AC \cdot AB}{2} \sin \alpha.$

Similarly the moment gravity force acting on AB is $\frac {g \rho\cdot AC \cdot AB}{2} \sin \beta.$

Therefore, equilibrium condition is $\alpha = \beta$ and the center of gravity of a homogeneous wire frame $ABC$ lies on each bisector of $\triangle DEF.$

This point is the incenter of the medial triangle $\triangle DEF.$

vladimir.shelomovskii@gmail.com, vvsss

Intersection of three cleavers

Cleaver.png

Prove that the Spieker center is located at the intersection of the three cleavers of triangle. A cleaver of a triangle is a line segment that bisects the perimeter of the triangle and has one endpoint at the midpoint of one of the three sides.

Proof

We use notation of previous proof. $DG$ is the segment contains the Spieker center, $G \in AB, \angle EDG = \angle FDG, H = DG \cap AC.$ WLOG, $AC > AB.$ \[DF||AC \implies \angle AHG = \angle FDG.\] Similarly, $\angle AGH = \angle EDG = \angle AHG.$

So $AH = AG \implies CH = AB + AH \implies DH$ is cleaver.

Therefore, the three cleavers meet at the Spieker center.

vladimir.shelomovskii@gmail.com, vvsss

Radical center of excircles

Radical center.png

Prove that the Spieker center of triangle is the radical center of the three excircles.

Proof

Let $\triangle ABC$ be given,$M_A, M_B, M_C$ be the midpoints of $BC, AC, BC,$ respectively.

Let $\omega_A, \omega_B, \omega_C$ be A-excircle, B-excircle, C-excircle centered at $X,Y,Z,$ respectively.

Let $I$ be the incenter of $\triangle ABC.$ Let $R_A$ be the radical axis of $\omega_B$ and $\omega_C, R_B$ be the radical axis of $\omega_A$ and $\omega_C, R_C$ be the radical axis of $\omega_B$ and $\omega_A,$ respectively.

It is known that the distances from $B$ to the tangent points of $\omega_C$ is equal to the distances from $C$ to the tangent points of $\omega_B, BM_A = CM_A$ therefore $M_A$ lies on the radical axis $R_A$ of $\omega_B$ and $\omega_C.$ Similarly, $M_B \in R_B, M_C \in R_C.$

$AI \perp ZY, R_A \perp XY \implies AI || RA \implies R_A$ is cleaver. Similarly, $R_B$ and $R_C$ are cleavers.

Therefore the radical center of the three excircles coinside with the intersection of the three cleavers of triangle.

vladimir.shelomovskii@gmail.com, vvsss

Nagel line

Nagel line.png

Let points $I, G, S$ be the incenter, the centroid and the Spieker center of triangle $\triangle ABC,$ respectively. Prove that points $I, G, S$ are collinear, $IG = 2 GS,$ and the barycentric coordinates of S are ${ b+c : c+a : a+b.}$

The Nagel line is the line on which points $I, G, S,$ and Nagel point $N$ lie.

Proof

Let $D, E, F$ be the midpoints of $BC, AC, BC,$ respectively. Bisector $AI$ is parallel to cleaver $DS, BI || ES.$ \[AB ||ED, \frac {AB}{DE} = 2 \implies \triangle ABI \sim \triangle DES \implies \frac {AI}{DS} = 2.\] Centroid $G$ divide the median $AD$ such that $\frac {AG}{DG} = 2 \implies$

$\triangle AGI \sim \triangle DGS \implies \frac {GI}{SG} = 2,$ and points $I, G, S$ are collinear.

The barycentric coordinates of $I$ are ${a : b : c}.$ The barycentric coordinates of $G$ are ${1 : 1 : 1}.$

\[\vec {GI} = 2 \vec {SG} \implies \vec {G} - \vec {I} = 2(\vec {S} - \vec {G}) \implies\] \[\vec {G} = \frac {3 \vec {G} - \vec {I} }{2} = {1 - \frac{a}{a+ b+c} : 1 - \frac {b}{a+b+c} : 1 - \frac{c}{a+b+c}} = { b+c : c+a : a+b.}\]

vladimir.shelomovskii@gmail.com, vvsss

Shatunov triangle

Shatunov triangle A.png

Let $\triangle ABC$ be given. Let $\omega, \omega_A, \omega_B, \omega_C$ be incircle, A-excircle, B-excircle, C-excircle centered at points $I,X,Y,Z,$ respectively.

Let $r_A = EF, r_B = DF, r_C = DE$ be the radical axes of the inscribed circle and one of the excircles of $\triangle ABC.$

The triangle $\triangle DEF$ whose sides are $r_A, r_B, r_C$ we name the Shatunov triangle. Accordingly, the vertices of the Shatunov triangle are the radical centers of a pair of excircles and an inscribed circle.

Prove:

a) the heights of the Shatunov triangle lie on the bisectors of the medial triangle. The orthocenter of the Shatunov triangle is the Steiner point of $\triangle ABC.$

b) The Shatunov triangle is homothetic to the anticomplementary triangle of $\triangle ABC$ with respect to the centroid $ABC$ with coefficient $\frac {1}{2}.$

Proof

a) Let $M_A, M_B, M_C$ be the midpoints of $BC, AC, AB,$ respectively.

The distances from $M_A$ to the tangent points of $\omega$ and $\omega_A$ are the same, so $M_A \in r_A.$ Similarly $M_B \in r_B, M_C \in r_C.$

Let $T$ and $T_Z$ be the points of tangency of $BC$ and $\omega_B$ and $\omega_C,$ respectively.

It is clear that $TC = BT_Z, BM_A = CM_A \implies M_A$ lies on the radical axis $R_A.$

Similarly, $M_B$ lies on the radical axis $R_B, M_C$ lies on the radical axis $R_C.$

$D = r_B \cap r_C \implies$ D is the radical center of $\omega, \omega_B, \omega_C \implies D \in R_A \implies R_A = DM_A.$

$AI \perp ZY, R_A \perp ZY, r_A \perp AI \implies DM_A \perp EF.$ Similarly $EM_B \perp DF, FM_C \perp DE.$

Therefore $DM_A, EM_B, FM_C$ are the heights of $\triangle DEF \implies S$ is the orthocenter of $\triangle DEF.$

$\triangle M_AM_BM_C$ is the medial triangle of $\triangle ABC, DSM_A$ is the bisector of $\angle M_BM_AM_C \implies S$ is the Steiner point of $\triangle ABC.$

b) $ZY || EF, XY || ED, ZX || FD \implies \triangle DEF \sim \triangle XYZ.$

$I$ is the orthocenter of $\triangle XYZ, S$ is the orthocenter of $\triangle DEF.$

Points $I, G,$ and $S,$ where $G$ is the centroid $ABC,$ are collinear, sides of is the $\triangle DEF$ are parallel to the respective sides of $\triangle XYZ \implies \triangle DEF$ is homothetic to the $\triangle XYZ$ with respect to $G.$

$IG = 2CS \implies$ the coefficient of homothety is $\frac {1}{2}.$

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Spieker_center&oldid=196628"