Difference between revisions of "2002 AIME I Problems/Problem 2"
(→Problem) |
m |
||
| Line 1: | Line 1: | ||
| − | |||
== Problem == | == Problem == | ||
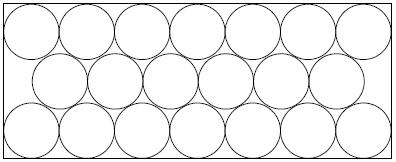
The diagram shows twenty congruent circles arranged in three rows and enclosed in a rectangle. The circles are tangent to one another and to the sides of the rectangle as shown in the diagram. The ratio of the longer dimension of the rectangle to the shorter dimension can be written as <math>\dfrac{1}{2}(\sqrt{p}-q)</math> where <math>p</math> and <math>q</math> are positive integers. Find <math>p+q</math>. | The diagram shows twenty congruent circles arranged in three rows and enclosed in a rectangle. The circles are tangent to one another and to the sides of the rectangle as shown in the diagram. The ratio of the longer dimension of the rectangle to the shorter dimension can be written as <math>\dfrac{1}{2}(\sqrt{p}-q)</math> where <math>p</math> and <math>q</math> are positive integers. Find <math>p+q</math>. | ||
| − | + | <center>[[Image:AIME_2002I_Problem_02.png]]</center> | |
== Solution == | == Solution == | ||
Revision as of 19:39, 3 November 2007
Problem
The diagram shows twenty congruent circles arranged in three rows and enclosed in a rectangle. The circles are tangent to one another and to the sides of the rectangle as shown in the diagram. The ratio of the longer dimension of the rectangle to the shorter dimension can be written as 
where 
and 
are positive integers. Find 
.
Solution
This problem needs a solution. If you have a solution for it, please help us out by adding it.
