Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2022 AIME I Problems/Problem 5"
 
(24 intermediate revisions by 6 users not shown)
Line 22: Line 22:
 
label("$\frac{D}{2} + 14m$", B--(550,264), N);
 
label("$\frac{D}{2} + 14m$", B--(550,264), N);
 
label("$D$", (0,0)--(550,0), S);
 
label("$D$", (0,0)--(550,0), S);
 +
label("$B$", B, N);
  
−
label("\textit{Upstream}", (550,132), W);
+
label("Downstream", (350,325), E);
 +
label("Upstream", (200,325), W);
 +
draw((225,325)--(325,325), Arrows);
 
</asy>
 
</asy>
 
(While it is indeed true that the triangle above with side lengths <math>60m</math>, <math>80m</math> and <math>D</math> is a right triangle, we do not know this yet, so we cannot assume this based on the diagram.)
 
(While it is indeed true that the triangle above with side lengths <math>60m</math>, <math>80m</math> and <math>D</math> is a right triangle, we do not know this yet, so we cannot assume this based on the diagram.)
  
−
By Pythagorean, we have
+
By the Pythagorean Theorem, we have
 
<cmath>\begin{align*}
 
<cmath>\begin{align*}
 
264^{2} + \left( \frac{D}{2} - 14m \right) ^{2} &= 3600m^{2} \\
 
264^{2} + \left( \frac{D}{2} - 14m \right) ^{2} &= 3600m^{2} \\
Line 44: Line 47:
 
~ihatemath123
 
~ihatemath123
  
−
== Solution 2 (Vectors) ==
+
== Solution 2 (Euclidean) ==
 +
<i><b>Claim</b></i>
 +
[[File:AIME 2022 I 5.png|450px|right]]
 +
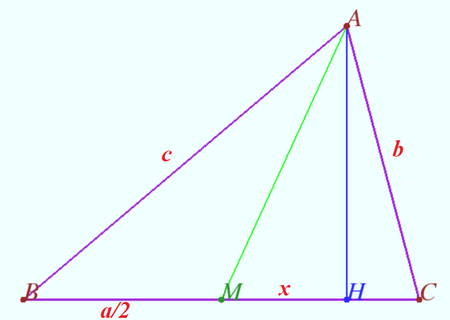
Median <math>AM</math> and altitude <math>AH</math> are drawn in triangle <math>ABC</math>.
 +
<math>AB = c, AC = b < c, BC = a</math> are known. Let's denote <math>MH = x</math>.
 +
 
 +
Prove that
 +
<cmath>\begin{align*}2ax = c^{2} - b^{2}\end{align*}</cmath>
 +
 
 +
<i><b>Proof</b></i>
 +
<cmath>BH + CH = a,</cmath>
 +
<cmath>\begin{align*} BH^{2} - CH^{2} = c^{2} - b^{2}\implies BH - CH &= \frac{c^{2} - b^{2}} {a},\end{align*}</cmath>
 +
<cmath>BH =  \frac{c^{2} - b^{2}}{2a} +  \frac{a}{2},</cmath>
 +
<cmath>\begin{align*}MH = BH - BM  &= \frac{c^{2} - b^{2}} {2a}.\end{align*}</cmath>
 +
 
 +
<i><b>Solution</b></i>
 +
 
 +
In the coordinate system associated with water, the movement is described by the scheme in the form of a triangle, the side on which Melanie floats is <math>80t</math>, where t is the time of  Melanie's movement, the side along which Sherry floats is <math>60t</math>.
 +
 
 +
The meeting point floated away at a distance of <math>14t</math> from the midpoint between the starting points of Melanie and Sherry.
 +
 
 +
In the notation of the <i><b>Claim</b></i>,
 +
<cmath>\begin{align*}  c = 80t, b = 60t, x = 14t \implies a = \frac{(80t)^2-(60t)^2}{2 \cdot 14t}=\frac{20^2}{4}\cdot \frac{16-9}{7}t = 100t.\end{align*}</cmath>
 +
Hence,
 +
<cmath>\begin{align*}  AH = \sqrt{BC^2-BH^2}= \sqrt{(80t)^2-(50t+14t)^2}=16t \cdot \sqrt{5^2-4^2}= 48t = 264 \implies t = 5.5.\end{align*}</cmath>
 +
<cmath> D = a = 100t = \boxed{550}</cmath>
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 
 +
== Solution 3 (Vectors) ==
 
We have the following diagram:
 
We have the following diagram:
 
<asy>
 
<asy>
Line 93: Line 124:
 
~MRENTHUSIASM
 
~MRENTHUSIASM
  
−
== Video Solution ==  
+
== Solution 4 (Vectors) ==
 +
 
 +
We can break down movement into two components: the <math>x</math>-component and the <math>y</math>-component. Suppose that Melanie travels a distance of <math>a</math> in the <math>x</math>-direction and a distance of <math>c</math> in the <math>y</math>-direction in one minute when there is no current. Similarly, suppose that Sherry travels a distance of <math>a</math> in the <math>x</math>-direction but a distance of <math>b</math> in the <math>y</math>-direction in one minute when there is no current. The current only affects the <math>x</math>-components because it goes in the <math>x</math>-direction.
 +
 
 +
<asy>
 +
/* Ruthlessly plagiarized from MRENTHUSIASM by Curious_crow */
 +
size(350);
 +
pair A, B, C;
 +
A = (0,264);
 +
B = (-275,0);
 +
C = (275,0);
 +
draw((-300,0)--(300,0)^^(-300,264)--(300,264)^^A--B^^A--C,linewidth(2));
 +
dot("Finish",A,1.75*N,linewidth(5));
 +
dot("Sherry",B,1.75*S,linewidth(5));
 +
dot("Melanie",C,1.75*S,linewidth(5));
 +
Label L1 = Label("$D$", align=(0,0), position=MidPoint, filltype=Fill(3,0,white));
 +
Label L2 = Label("$264$", align=(0,0), position=MidPoint, filltype=Fill(0,3,white));
 +
Label L3 = Label("Current $(14)$", position=EndPoint, filltype=Fill(3,0,white));
 +
Label L4 = Label("$a$", align=(-1,0), position=Relative(0.4));
 +
Label L5 = Label("$b+14$", align=(0,1), position=Relative(0.4));
 +
Label L6 = Label("$a$", align=(1,0), position=Relative(0.4));
 +
Label L7 = Label("$c-14$", align=(0,1), position=Relative(0.4));
 +
draw(B-(0,75)--C-(0,75), L=L1, arrow=Arrows(),bar=Bars(15));
 +
draw((-350,0)--(-350,264), L=L2, arrow=Arrows(),bar=Bars(15));
 +
draw((-300,-120)--(300,-120), L=L3, arrow=EndArrow());
 +
draw(B--B+(0,48), L=L4, arrow=EndArrow());
 +
draw(B+(0,48)--B+(50,48), L=L5, arrow=EndArrow());
 +
draw(C--C+(0,48), L=L6, arrow=EndArrow());
 +
draw(C+(0,48)--C+(-50,48), L=L7, arrow=EndArrow());
 +
</asy>
 +
 
 +
Now, note that <math>a^2 + b^2 = 60^2</math> because Sherry travels 60 meters in a minute. Thus, <math>a^2 + c^2 = 80^2</math> because Melanie travels 80 meters in a minute. Also, the distance they travel with the current must be the same in one minute because they reach the point equidistant from them at the same time. That means <math>b + 14 = c - 14</math> or <math>b = c - 28</math>. So now we can plug that into the two equations to get:
 +
<cmath>\begin{align*}
 +
a^2 + c^2 &= 80^2, \\
 +
a^2 + (c-28)^2 &= 60^2.
 +
\end{align*}</cmath>
 +
We can solve the system of equations to get <math>a = 48</math> and <math>c = 64</math>. From this, we can figure out that it must've taken them <math>5.5</math> minutes to get to the other side, because <math>264/48 = 5.5</math>. This means that there are <math>5.5</math> lengths of <math>48</math> in each person's travel. Also, <math>D</math> must be equal to <math>11(b+14) = 11(c-14) </math> because there are <math>(5.5)2 = 11</math> lengths of <math>b-14</math> between them, <math>5.5</math> on each person's side. Since <math>c = 64</math>, we have <math>c-14 = 50</math>, so the answer is <cmath>D=11\cdot50=\boxed{550}.</cmath>
 +
~Curious_crow
 +
 
 +
== Video Solution 1 ==  
  
 
https://youtu.be/MJ_M-xvwHLk?t=1487
 
https://youtu.be/MJ_M-xvwHLk?t=1487
  
 
~ThePuzzlr
 
~ThePuzzlr
 +
 +
== Video Solution 2 ==
 +
 +
https://www.youtube.com/watch?v=s6nXXnBLTdA
 +
 +
~Chickenugget
 +
 +
== Video Solution 3 ==
 +
 +
https://youtu.be/XAe8AkmHexw
 +
 +
~AMC & AIME Training
  
 
==See Also==
 
==See Also==
 
{{AIME box|year=2022|n=I|num-b=4|num-a=6}}
 
{{AIME box|year=2022|n=I|num-b=4|num-a=6}}

Latest revision as of 13:35, 23 February 2023

Problem

A straight river that is $264$ meters wide flows from west to east at a rate of $14$ meters per minute. Melanie and Sherry sit on the south bank of the river with Melanie a distance of $D$ meters downstream from Sherry. Relative to the water, Melanie swims at $80$ meters per minute, and Sherry swims at $60$ meters per minute. At the same time, Melanie and Sherry begin swimming in straight lines to a point on the north bank of the river that is equidistant from their starting positions. The two women arrive at this point simultaneously. Find $D$.

Solution 1 (Euclidean)

Define $m$ as the number of minutes they swim for.

Let their meeting point be $A$. Melanie is swimming against the current, so she must aim upstream from point $A$, to compensate for this; in particular, since she is swimming for $m$ minutes, the current will push her $14m$ meters downstream in that time, so she must aim for a point $B$ that is $14m$ meters upstream from point $A$. Similarly, Sherry is swimming downstream for $m$ minutes, so she must also aim at point $B$ to compensate for the flow of the current.

If Melanie and Sherry were to both aim at point $B$ in a currentless river with the same dimensions, they would still both meet at that point simultaneously. Since there is no current in this scenario, the distances that Melanie and Sherry travel, respectively, are $80m$ and $60m$ meters. We can draw out this new scenario, with the dimensions that we have: [asy] unitsize(0.02cm); draw((0,0)--(0,264)--(550,264)--(550,0)--cycle); pair B = (198,264); dot(B^^(0,0)^^(550,0),linewidth(5)); draw((0,0)--B,dashed); draw((550,0)--B,dashed); label("$60m$", (0,0)--B, E); label("$80m$", (550,0)--B, W); label("$264$", (0,0)--(0,264), W); label("$\frac{D}{2} - 14m$", (0,264)--B, N); label("$\frac{D}{2} + 14m$", B--(550,264), N); label("$D$", (0,0)--(550,0), S); label("$B$", B, N); label("Downstream", (350,325), E); label("Upstream", (200,325), W); draw((225,325)--(325,325), Arrows); [/asy] (While it is indeed true that the triangle above with side lengths $60m$, $80m$ and $D$ is a right triangle, we do not know this yet, so we cannot assume this based on the diagram.)

By the Pythagorean Theorem, we have \begin{align*} 264^{2} + \left( \frac{D}{2} - 14m \right) ^{2} &= 3600m^{2} \\ 264^{2} + \left( \frac{D}{2} + 14m \right) ^{2} &= 6400m^{2}. \end{align*}

Subtracting the first equation from the second gives us $28Dm = 2800m^{2}$, so $D = 100m$. Substituting this into our first equation, we have that \begin{align*}264^{2} + 36^{2} m^{2} &= 60^{2}m^{2} \\ 264^{2} &= 96 \cdot 24 \cdot m^{2} \\ 11^{2} &= 4 \cdot m^{2} \\ m &= \frac{11}{2}. \end{align*}

So $D = 100m = \boxed{550}$.

~ihatemath123

Solution 2 (Euclidean)

Claim

AIME 2022 I 5.png

Median $AM$ and altitude $AH$ are drawn in triangle $ABC$. $AB = c, AC = b < c, BC = a$ are known. Let's denote $MH = x$.

Prove that \begin{align*}2ax = c^{2} - b^{2}\end{align*}

Proof \[BH + CH = a,\] \begin{align*} BH^{2} - CH^{2} = c^{2} - b^{2}\implies BH - CH &= \frac{c^{2} - b^{2}} {a},\end{align*} \[BH = \frac{c^{2} - b^{2}}{2a} + \frac{a}{2},\] \begin{align*}MH = BH - BM &= \frac{c^{2} - b^{2}} {2a}.\end{align*}

Solution

In the coordinate system associated with water, the movement is described by the scheme in the form of a triangle, the side on which Melanie floats is $80t$, where t is the time of Melanie's movement, the side along which Sherry floats is $60t$.

The meeting point floated away at a distance of $14t$ from the midpoint between the starting points of Melanie and Sherry.

In the notation of the Claim, \begin{align*} c = 80t, b = 60t, x = 14t \implies a = \frac{(80t)^2-(60t)^2}{2 \cdot 14t}=\frac{20^2}{4}\cdot \frac{16-9}{7}t = 100t.\end{align*} Hence, \begin{align*} AH = \sqrt{BC^2-BH^2}= \sqrt{(80t)^2-(50t+14t)^2}=16t \cdot \sqrt{5^2-4^2}= 48t = 264 \implies t = 5.5.\end{align*} \[D = a = 100t = \boxed{550}\] vladimir.shelomovskii@gmail.com, vvsss

Solution 3 (Vectors)

We have the following diagram: [asy] /* Made by MRENTHUSIASM */ size(350); pair A, B, C; A = (0,264); B = (-275,0); C = (275,0); draw((-300,0)--(300,0)^^(-300,264)--(300,264)^^A--B^^A--C,linewidth(2)); dot("Finish",A,1.75*N,linewidth(5)); dot("Sherry",B,1.75*S,linewidth(5)); dot("Melanie",C,1.75*S,linewidth(5)); Label L1 = Label("$D$", align=(0,0), position=MidPoint, filltype=Fill(3,0,white)); Label L2 = Label("$264$", align=(0,0), position=MidPoint, filltype=Fill(0,3,white)); Label L3 = Label("Current $(14)$", position=EndPoint, filltype=Fill(3,0,white)); Label L4 = Label("$y$", align=(-1,0), position=Relative(0.4)); Label L5 = Label("$x$", align=(0,1), position=Relative(0.4)); Label L6 = Label("$y$", align=(1,0), position=Relative(0.4)); Label L7 = Label("$x$", align=(0,1), position=Relative(0.4)); draw(B-(0,75)--C-(0,75), L=L1, arrow=Arrows(),bar=Bars(15)); draw((-350,0)--(-350,264), L=L2, arrow=Arrows(),bar=Bars(15)); draw((-300,-120)--(300,-120), L=L3, arrow=EndArrow()); draw(B--B+(0,48), L=L4, arrow=EndArrow()); draw(B+(0,48)--B+(50,48), L=L5, arrow=EndArrow()); draw(C--C+(0,48), L=L6, arrow=EndArrow()); draw(C+(0,48)--C+(-50,48), L=L7, arrow=EndArrow()); [/asy] Since Melanie and Sherry swim for the same distance and the same amount of time, they swim at the same net speed.

Let $x$ and $y$ be some positive numbers. We have the following table: \[\begin{array}{c||c|c|c} & \textbf{Net Velocity Vector (m/min)} & \textbf{Natural Velocity Vector (m/min)} & \textbf{Natural Speed (m/min)} \\ \hline \hline &&& \\ [-2.25ex] \textbf{Melanie} & \langle -x,y\rangle & \langle -x-14,y\rangle & 80 \\ \hline &&& \\ [-2.25ex] \textbf{Sherry} & \langle x,y\rangle & \langle x-14,y\rangle & 60 \end{array}\] Recall that $|\text{velocity}|=\text{speed},$ so \begin{align*} (-x-14)^2 + y^2 &= 80^2, &&(1) \\ (x-14)^2 + y^2 &= 60^2. &&(2) \end{align*} We subtract $(2)$ from $(1)$ to get $56x=2800,$ from which $x=50.$ Substituting this into either equation, we have $y=48.$

It follows that Melanie and Sherry both swim for $264\div y=5.5$ minutes. Therefore, the answer is \[D=2x\cdot5.5=\boxed{550}.\] ~MRENTHUSIASM

Solution 4 (Vectors)

We can break down movement into two components: the $x$-component and the $y$-component. Suppose that Melanie travels a distance of $a$ in the $x$-direction and a distance of $c$ in the $y$-direction in one minute when there is no current. Similarly, suppose that Sherry travels a distance of $a$ in the $x$-direction but a distance of $b$ in the $y$-direction in one minute when there is no current. The current only affects the $x$-components because it goes in the $x$-direction.

[asy] /* Ruthlessly plagiarized from MRENTHUSIASM by Curious_crow */ size(350); pair A, B, C; A = (0,264); B = (-275,0); C = (275,0); draw((-300,0)--(300,0)^^(-300,264)--(300,264)^^A--B^^A--C,linewidth(2)); dot("Finish",A,1.75*N,linewidth(5)); dot("Sherry",B,1.75*S,linewidth(5)); dot("Melanie",C,1.75*S,linewidth(5)); Label L1 = Label("$D$", align=(0,0), position=MidPoint, filltype=Fill(3,0,white)); Label L2 = Label("$264$", align=(0,0), position=MidPoint, filltype=Fill(0,3,white)); Label L3 = Label("Current $(14)$", position=EndPoint, filltype=Fill(3,0,white)); Label L4 = Label("$a$", align=(-1,0), position=Relative(0.4)); Label L5 = Label("$b+14$", align=(0,1), position=Relative(0.4)); Label L6 = Label("$a$", align=(1,0), position=Relative(0.4)); Label L7 = Label("$c-14$", align=(0,1), position=Relative(0.4)); draw(B-(0,75)--C-(0,75), L=L1, arrow=Arrows(),bar=Bars(15)); draw((-350,0)--(-350,264), L=L2, arrow=Arrows(),bar=Bars(15)); draw((-300,-120)--(300,-120), L=L3, arrow=EndArrow()); draw(B--B+(0,48), L=L4, arrow=EndArrow()); draw(B+(0,48)--B+(50,48), L=L5, arrow=EndArrow()); draw(C--C+(0,48), L=L6, arrow=EndArrow()); draw(C+(0,48)--C+(-50,48), L=L7, arrow=EndArrow()); [/asy]

Now, note that $a^2 + b^2 = 60^2$ because Sherry travels 60 meters in a minute. Thus, $a^2 + c^2 = 80^2$ because Melanie travels 80 meters in a minute. Also, the distance they travel with the current must be the same in one minute because they reach the point equidistant from them at the same time. That means $b + 14 = c - 14$ or $b = c - 28$. So now we can plug that into the two equations to get: \begin{align*} a^2 + c^2 &= 80^2, \\ a^2 + (c-28)^2 &= 60^2. \end{align*} We can solve the system of equations to get $a = 48$ and $c = 64$. From this, we can figure out that it must've taken them $5.5$ minutes to get to the other side, because $264/48 = 5.5$. This means that there are $5.5$ lengths of $48$ in each person's travel. Also, $D$ must be equal to $11(b+14) = 11(c-14)$ because there are $(5.5)2 = 11$ lengths of $b-14$ between them, $5.5$ on each person's side. Since $c = 64$, we have $c-14 = 50$, so the answer is \[D=11\cdot50=\boxed{550}.\] ~Curious_crow

Video Solution 1

https://youtu.be/MJ_M-xvwHLk?t=1487

~ThePuzzlr

Video Solution 2

https://www.youtube.com/watch?v=s6nXXnBLTdA

~Chickenugget

Video Solution 3

https://youtu.be/XAe8AkmHexw

~AMC & AIME Training

See Also

2022 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 4 		Followed by
Problem 6
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2022_AIME_I_Problems/Problem_5&oldid=190174"