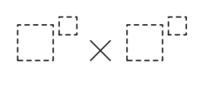Difference between revisions of "2023 AMC 8 Problems/Problem 6"
(→Solution 2) |
Irorlpiggy (talk | contribs) |
||
| Line 15: | Line 15: | ||
~apex304 (SohumUttamchandani, wuwang2002, TaeKim, Cxrupptedpat, stevens0209 (editing)) | ~apex304 (SohumUttamchandani, wuwang2002, TaeKim, Cxrupptedpat, stevens0209 (editing)) | ||
| + | |||
| + | ==Video Solution by Magic Square== | ||
| + | https://youtu.be/-N46BeEKaCQ?t=5247 | ||
==See Also== | ==See Also== | ||
{{AMC8 box|year=2023|num-b=5|num-a=7}} | {{AMC8 box|year=2023|num-b=5|num-a=7}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 10:48, 25 January 2023
Problem
The digits 2, 0, 2, and 3 are placed in the expression below, one digit per box. What is the maximum possible value of the expression?
![]()
Solution 1
First, let us consider the cases where ![]() is a base. This would result in the entire expression being
is a base. This would result in the entire expression being ![]() . However, if
. However, if ![]() is an exponent, we will get a value greater than
is an exponent, we will get a value greater than ![]() . As
. As ![]() is greater than
is greater than ![]() and
and ![]() , the answer is
, the answer is ![]() .
.
~MathFun1000
Solution 2
The maximum possible value of using the digit ![]() . We can maximize our value by keeping the
. We can maximize our value by keeping the ![]() and
and ![]() together in one power. (Biggest with biggest and smallest with smallest) This shows
together in one power. (Biggest with biggest and smallest with smallest) This shows ![]() =
=![]() =
=![]() . (Don't want
. (Don't want ![]() cause that's
cause that's ![]() ) It is going to be
) It is going to be ![]()
~apex304 (SohumUttamchandani, wuwang2002, TaeKim, Cxrupptedpat, stevens0209 (editing))
Video Solution by Magic Square
https://youtu.be/-N46BeEKaCQ?t=5247
See Also
| 2023 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 5 |
Followed by Problem 7 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.