Difference between revisions of "Miquel's point"
(→Miquel and Steiner's quadrilateral theorem) |
(→Miquel and Steiner's quadrilateral theorem) |
||
| Line 1: | Line 1: | ||
==Miquel and Steiner's quadrilateral theorem== | ==Miquel and Steiner's quadrilateral theorem== | ||
| − | [[Miquel circles|500px|right]] | + | [[File:4 Miquel circles.png|500px|right]] |
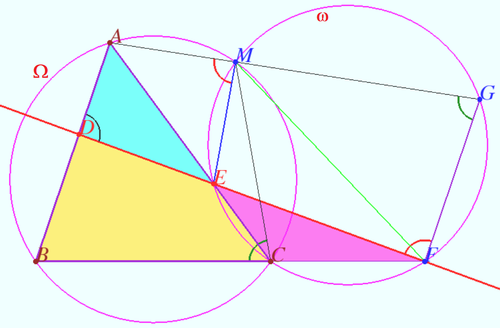
Let four lines made four triangles of a complete quadrilateral. In the diagram these are <math>\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.</math> | Let four lines made four triangles of a complete quadrilateral. In the diagram these are <math>\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.</math> | ||
| Line 7: | Line 7: | ||
<i><b>Proof</b></i> | <i><b>Proof</b></i> | ||
| − | Let circumcircle of <math>\triangle ABC</math> circle <math>\Omega</math> cross the circumcircle of <math>\triangle CEF \omega</math> at point <math>M.</math> | + | Let circumcircle of <math>\triangle ABC</math> circle <math>\Omega</math> cross the circumcircle of <math>\triangle CEF</math> circle <math>\omega</math> at point <math>M.</math> |
Let <math>AM</math> cross <math>\omega</math> second time in the point <math>G.</math> | Let <math>AM</math> cross <math>\omega</math> second time in the point <math>G.</math> | ||
| Line 13: | Line 13: | ||
<math>CMGF</math> is cyclic <math>\implies \angle BCM = \angle MGF.</math> | <math>CMGF</math> is cyclic <math>\implies \angle BCM = \angle MGF.</math> | ||
| − | <math>AMCB</math> is cyclic <math>\implies \angle BCM + \angle BAM = 180^\circ \implies \angle BAG + \angle AGF = 180^\circ \implies AB||GF.</math> | + | <math>AMCB</math> is cyclic <math>\implies \angle BCM + \angle BAM = 180^\circ \implies</math> |
| + | |||
| + | <math>\angle BAG + \angle AGF = 180^\circ \implies AB||GF.</math> | ||
<math>CMGF</math> is cyclic <math>\implies \angle AME = \angle EFG.</math> | <math>CMGF</math> is cyclic <math>\implies \angle AME = \angle EFG.</math> | ||
| − | <math>AD||GF \implies \angle ADE + \angle DFG = 180^\circ \implies \angle ADE + \angle AME = 180^\circ \implies ADEM</math> is cyclic and circumcircle of <math>\triangle ADE</math> contain the point <math>M.</math> | + | <math>AD||GF \implies \angle ADE + \angle DFG = 180^\circ \implies \angle ADE + \angle AME = 180^\circ \implies</math> |
| + | |||
| + | <math>ADEM</math> is cyclic and circumcircle of <math>\triangle ADE</math> contain the point <math>M.</math> | ||
Similarly circumcircle of <math>\triangle BDF</math> contain the point <math>M</math> as desired. | Similarly circumcircle of <math>\triangle BDF</math> contain the point <math>M</math> as desired. | ||
Revision as of 09:18, 5 December 2022
Miquel and Steiner's quadrilateral theorem
Let four lines made four triangles of a complete quadrilateral. In the diagram these are ![]()
Prove that the circumcircles of all four triangles meet at a single point.
Proof
Let circumcircle of ![]() circle
circle ![]() cross the circumcircle of
cross the circumcircle of ![]() circle
circle ![]() at point
at point ![]()
Let ![]() cross
cross ![]() second time in the point
second time in the point ![]()
![]() is cyclic
is cyclic ![]()
![]() is cyclic
is cyclic ![]()
![]()
![]() is cyclic
is cyclic ![]()
![]()
![]() is cyclic and circumcircle of
is cyclic and circumcircle of ![]() contain the point
contain the point ![]()
Similarly circumcircle of ![]() contain the point
contain the point ![]() as desired.
as desired.
vladimir.shelomovskii@gmail.com, vvsss
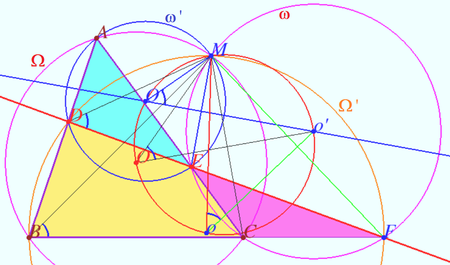
Circle of circumcenters
Let four lines made four triangles of a complete quadrilateral. In the diagram these are ![]()
Prove that the circumcenters of all four triangles and point ![]() are concyclic.
are concyclic.
Proof
Let ![]() and
and ![]() be the circumcircles of
be the circumcircles of ![]() and
and ![]() respectively.
respectively.
In ![]()
In ![]()
![]() is the common chord of
is the common chord of ![]() and
and ![]()
![]()
Similarly, ![]() is the common chord of
is the common chord of ![]() and
and ![]()
Similarly, ![]() is the common chord of
is the common chord of ![]() and
and ![]()
![]() points
points ![]() and
and ![]() are concyclic as desired.
are concyclic as desired.
vladimir.shelomovskii@gmail.com, vvsss