Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2016 USAMO Problems/Problem 3"

(→‎Solution)
(→‎See also)
 
(23 intermediate revisions by 3 users not shown)
Line 8: Line 8:
 
1. Let <math>I_A</math> be the <math>A</math>-excenter, then <math>I_A,O,</math> and <math>P</math> are colinear. This can be proved by the Trigonometric Form of Ceva's Theorem for <math>\triangle I_AI_BI_C.</math>
 
1. Let <math>I_A</math> be the <math>A</math>-excenter, then <math>I_A,O,</math> and <math>P</math> are colinear. This can be proved by the Trigonometric Form of Ceva's Theorem for <math>\triangle I_AI_BI_C.</math>
  
−
2. Show that <math>I_AY^2-I_AZ^2=OY^2-OZ^2,</math> which shows <math>\overline{OI_A}\perp\overline{YZ}.</math> This can be proved by multiple applications of the Pythagorean Thm.
+
2. Show that <math>I_AY^2-I_AZ^2=OY^2-OZ^2,</math> which implies <math>\overline{OI_A}\perp\overline{YZ}.</math> This can be proved by multiple applications of the Pythagorean Thm.
  
−
{{MAA Notice}}
+
==Solution 2==
 +
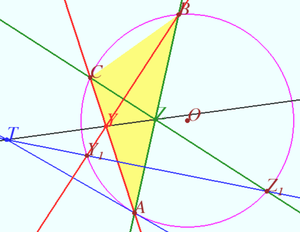
[[File:2016 USAMO 3a.png|300px|right]]
 +
We find point <math>T</math> on line <math>YZ,</math> we prove that <math>TY \perp OI_A</math> and state that <math>P</math> is the point <math>X(24)</math> from ENCYCLOPEDIA OF TRIANGLE, therefore <math>P \in OI_A.</math>
 +
 
 +
Let <math>\omega</math> be circumcircle of <math>\triangle ABC</math> centered at <math>O.</math>
 +
Let <math>Y_1,</math> and <math>Z_1</math> be crosspoints of <math>\omega</math> and <math>BY,</math> and <math>CZ,</math> respectively.
 +
Let <math>T</math> be crosspoint of <math>YZ</math> and <math>Y_1 Z_1.</math>
 +
In accordance the Pascal theorem for pentagon <math>AZ_1BCY_1,</math> <math>AT</math> is tangent to <math>\omega</math> at <math>A.</math>
 +
 
 +
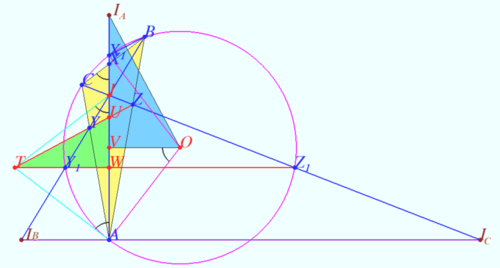
[[File:2016 USAMO 3b.png|500px|right]]
 +
Let <math>I_A, I_B, I_C</math> be <math>A, B,</math> and <math>C</math>-excenters of <math>\triangle ABC.</math>
 +
Denote <cmath>a = BC, b = AC, c = AB, 2\alpha = \angle CAB, 2\beta = \angle ABC, 2\gamma = \angle ACB,</cmath>
 +
<cmath>\psi = 90^\circ – \gamma + \beta, X = AI_A \cap \omega, X_1 = BC \cap AI_A,</cmath>
 +
<cmath>I = BI_B  \cap CI_C, U= YZ \cap AI_A, W = Y_1Z_1 \cap AI_A,</cmath>
 +
<math>V</math> is the foot ot perpendicular from <math>O</math> to <math>AI_A.</math>
 +
 +
<math>I</math> is ortocenter of <math>\triangle I_A I_B I_C</math> and incenter of <math>\triangle ABC.</math>
 +
 
 +
<math>\omega</math> is the Nine–point circle of <math>\triangle I_A I_B I_C.</math>
 +
 
 +
<math>Y_1</math> is the midpoint of <math>II_B, Z_1</math> is the midpoint of <math>II_C</math> in accordance with property of Nine–point circle <math>\implies</math>
 +
<cmath>Y_1Z_1 || I_B AI_C || VO, IW = AW \implies TW \perp AI.</cmath>
 +
<cmath>\angle AXC = 180 ^\circ – 2\gamma – \alpha = 90 ^\circ – \gamma + \beta = \psi.</cmath>
 +
<cmath>\angle TAI = \angle VOA = 2\beta + \alpha = 90 ^\circ – \gamma + \beta = \psi.</cmath>
 +
<cmath>I_A X_1 = IX_1 = BX_1 = 2R \sin \alpha \implies</cmath>
 +
<cmath>\cot \angle OI_A A = \frac {VI_A}{VO} = \frac {R \sin \psi + 2R \sin \alpha}{R \cos \psi} = \tan \psi + \frac{2 \sin\alpha}{\cos \psi}.</cmath>
 +
<cmath>CX = \frac {ab}{b+c} \implies \frac {AI}{IX}= \frac {AC}{CX}= \frac {b+c}{a} \implies AI = AX \frac {b+c}{a+b+c},</cmath>
 +
<cmath>AW = \frac {AI}{2}, UW = AU – AW,</cmath>
 +
In <math>\triangle ABC</math> segment <math>YZ</math> cross segment <math>AX \implies \frac {AU}{UX} = \frac {m + nk}{k+1},</math> where <math>n = \frac {a}{b}, m = \frac{a}{c}, k=\frac {b}{c},</math>
 +
<cmath>\frac {AU}{UX} = \frac{2a}{b+c} \implies  AU = AX \cdot \frac {b+c}{2a +b +c}.</cmath>
 +
<cmath>\frac {AU – AW}{AW} = \frac {b+c} {2a + b + c}.</cmath>
 +
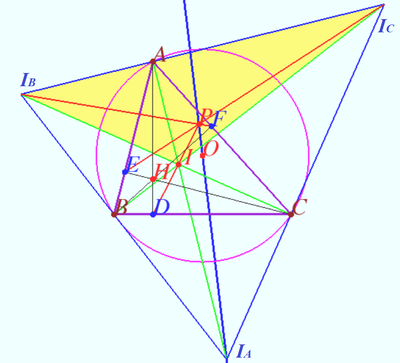
[[File:2016 USAMO 3c.png|400px|right]]
 +
<cmath>\cot \angle UTW = \frac {TW}{UW} = \frac {AW \cdot \tan \psi}{AU – AW} = \tan \psi \cdot \frac {2a +b+c}{b+c} =</cmath>
 +
<cmath>=\tan \psi \cdot \frac {2a}{b+c} + \tan \psi = \frac {2 \sin \alpha}{\sin \psi} \tan \psi + \tan \psi  = \tan \psi + \frac{2 \sin\alpha}{\cos \psi}</cmath>
 +
<cmath>\implies  \angle UTW = \angle OI_AA .</cmath>
 +
<cmath>TW \perp AI_A \implies TYZ \perp OI_A.</cmath>
 +
 
 +
Let <math>\triangle II_B I_C</math> be the base triangle with orthocenter <math>I_A,</math> center of Nine-points circle <math>O \implies OI_A</math> be the Euler line of <math>\triangle II_B I_C.</math>
 +
 
 +
<math>\triangle ABC</math> is orthic triangle of <math>\triangle II_B I_C,</math>
 +
 
 +
<math>\triangle DEF</math> is orthic-of-orthic triangle.
 +
 
 +
<math>P</math> is perspector of base triangle and orthic-of-orthic triangle.
 +
 
 +
Therefore <math>P</math> is point <math>X(24)</math> of ENCYCLOPEDIA OF TRIANGLE CENTERS which lies on Euler line of the base triangle.
 +
[[https://artofproblemsolving.com/wiki/index.php/Kimberling%E2%80%99s_point_X(24)]]
 +
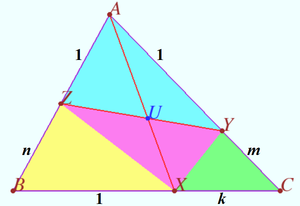
[[File:2016 USAMO 3d.png|300px|right]]
 +
 
 +
<i><b>Claim</b></i>    <cmath>\frac {AU}{UX} = \frac {m + nk}{k + 1}.</cmath>       
 +
<i><b>Proof</b></i> 
 +
<cmath>\frac {[AYZ]}{[ABC]} = \frac {AZ \cdot AY}{AB \cdot AC} = \frac {1}{(n + 1) \cdot (m+1)}, </cmath>
 +
<cmath>\frac {[BXZ]}{[ABC]} = \frac {BZ \cdot BX}{AB \cdot BC} = \frac {n}{(n + 1) \cdot (k+1)}, </cmath>
 +
<cmath>\frac {[CXY]}{[ABC]} = \frac {CY \cdot CX}{AC \cdot BC} = \frac {mk}{(m + 1) \cdot (k+1)},</cmath>
 +
<cmath>\frac {[XYZ]}{[ABC]} = 1 - \frac {[AYZ]}{[ABC]} – \frac {[BXZ]}{[ABC]} – \frac {[CXY]}{[ABC]}  = \frac {m+nk}{(m + 1) \cdot (k+1)\cdot (n+1)}, </cmath>
 +
<cmath>\frac {AU}{UX} = \frac {[AYZ]}{[XYZ]} = \frac {m + nk}{k + 1}.</cmath>
 +
 
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
  
 
==See also==
 
==See also==
 
{{USAMO newbox|year=2016|num-b=2|num-a=4}}
 
{{USAMO newbox|year=2016|num-b=2|num-a=4}}
 +
 +
{{MAA Notice}}

Latest revision as of 20:36, 17 October 2022

Problem

Let $\triangle ABC$ be an acute triangle, and let $I_B, I_C,$ and $O$ denote its $B$-excenter, $C$-excenter, and circumcenter, respectively. Points $E$ and $Y$ are selected on $\overline{AC}$ such that $\angle ABY = \angle CBY$ and $\overline{BE}\perp\overline{AC}.$ Similarly, points $F$ and $Z$ are selected on $\overline{AB}$ such that $\angle ACZ = \angle BCZ$ and $\overline{CF}\perp\overline{AB}.$

Lines $I_B F$ and $I_C E$ meet at $P.$ Prove that $\overline{PO}$ and $\overline{YZ}$ are perpendicular.

Solution

This problem can be proved in the following two steps.

1. Let $I_A$ be the $A$-excenter, then $I_A,O,$ and $P$ are colinear. This can be proved by the Trigonometric Form of Ceva's Theorem for $\triangle I_AI_BI_C.$

2. Show that $I_AY^2-I_AZ^2=OY^2-OZ^2,$ which implies $\overline{OI_A}\perp\overline{YZ}.$ This can be proved by multiple applications of the Pythagorean Thm.

Solution 2

2016 USAMO 3a.png

We find point $T$ on line $YZ,$ we prove that $TY \perp OI_A$ and state that $P$ is the point $X(24)$ from ENCYCLOPEDIA OF TRIANGLE, therefore $P \in OI_A.$

Let $\omega$ be circumcircle of $\triangle ABC$ centered at $O.$ Let $Y_1,$ and $Z_1$ be crosspoints of $\omega$ and $BY,$ and $CZ,$ respectively. Let $T$ be crosspoint of $YZ$ and $Y_1 Z_1.$ In accordance the Pascal theorem for pentagon $AZ_1BCY_1,$ $AT$ is tangent to $\omega$ at $A.$

2016 USAMO 3b.png

Let $I_A, I_B, I_C$ be $A, B,$ and $C$-excenters of $\triangle ABC.$ Denote \[a = BC, b = AC, c = AB, 2\alpha = \angle CAB, 2\beta = \angle ABC, 2\gamma = \angle ACB,\] \[\psi = 90^\circ – \gamma + \beta, X = AI_A \cap \omega, X_1 = BC \cap AI_A,\] \[I = BI_B \cap CI_C, U= YZ \cap AI_A, W = Y_1Z_1 \cap AI_A,\] $V$ is the foot ot perpendicular from $O$ to $AI_A.$

$I$ is ortocenter of $\triangle I_A I_B I_C$ and incenter of $\triangle ABC.$

$\omega$ is the Nine–point circle of $\triangle I_A I_B I_C.$

$Y_1$ is the midpoint of $II_B, Z_1$ is the midpoint of $II_C$ in accordance with property of Nine–point circle $\implies$ \[Y_1Z_1 || I_B AI_C || VO, IW = AW \implies TW \perp AI.\] \[\angle AXC = 180 ^\circ – 2\gamma – \alpha = 90 ^\circ – \gamma + \beta = \psi.\] \[\angle TAI = \angle VOA = 2\beta + \alpha = 90 ^\circ – \gamma + \beta = \psi.\] \[I_A X_1 = IX_1 = BX_1 = 2R \sin \alpha \implies\] \[\cot \angle OI_A A = \frac {VI_A}{VO} = \frac {R \sin \psi + 2R \sin \alpha}{R \cos \psi} = \tan \psi + \frac{2 \sin\alpha}{\cos \psi}.\] \[CX = \frac {ab}{b+c} \implies \frac {AI}{IX}= \frac {AC}{CX}= \frac {b+c}{a} \implies AI = AX \frac {b+c}{a+b+c},\] \[AW = \frac {AI}{2}, UW = AU – AW,\] In $\triangle ABC$ segment $YZ$ cross segment $AX \implies \frac {AU}{UX} = \frac {m + nk}{k+1},$ where $n = \frac {a}{b}, m = \frac{a}{c}, k=\frac {b}{c},$ \[\frac {AU}{UX} = \frac{2a}{b+c} \implies AU = AX \cdot \frac {b+c}{2a +b +c}.\] \[\frac {AU – AW}{AW} = \frac {b+c} {2a + b + c}.\]

2016 USAMO 3c.png

\[\cot \angle UTW = \frac {TW}{UW} = \frac {AW \cdot \tan \psi}{AU – AW} = \tan \psi \cdot \frac {2a +b+c}{b+c} =\] \[=\tan \psi \cdot \frac {2a}{b+c} + \tan \psi = \frac {2 \sin \alpha}{\sin \psi} \tan \psi + \tan \psi = \tan \psi + \frac{2 \sin\alpha}{\cos \psi}\] \[\implies \angle UTW = \angle OI_AA .\] \[TW \perp AI_A \implies TYZ \perp OI_A.\]

Let $\triangle II_B I_C$ be the base triangle with orthocenter $I_A,$ center of Nine-points circle $O \implies OI_A$ be the Euler line of $\triangle II_B I_C.$

$\triangle ABC$ is orthic triangle of $\triangle II_B I_C,$

$\triangle DEF$ is orthic-of-orthic triangle.

$P$ is perspector of base triangle and orthic-of-orthic triangle.

Therefore $P$ is point $X(24)$ of ENCYCLOPEDIA OF TRIANGLE CENTERS which lies on Euler line of the base triangle. [[1]]

2016 USAMO 3d.png

Claim \[\frac {AU}{UX} = \frac {m + nk}{k + 1}.\] Proof \[\frac {[AYZ]}{[ABC]} = \frac {AZ \cdot AY}{AB \cdot AC} = \frac {1}{(n + 1) \cdot (m+1)},\] \[\frac {[BXZ]}{[ABC]} = \frac {BZ \cdot BX}{AB \cdot BC} = \frac {n}{(n + 1) \cdot (k+1)},\] \[\frac {[CXY]}{[ABC]} = \frac {CY \cdot CX}{AC \cdot BC} = \frac {mk}{(m + 1) \cdot (k+1)},\] \[\frac {[XYZ]}{[ABC]} = 1 - \frac {[AYZ]}{[ABC]} – \frac {[BXZ]}{[ABC]} – \frac {[CXY]}{[ABC]} = \frac {m+nk}{(m + 1) \cdot (k+1)\cdot (n+1)},\] \[\frac {AU}{UX} = \frac {[AYZ]}{[XYZ]} = \frac {m + nk}{k + 1}.\]

vladimir.shelomovskii@gmail.com, vvsss

See also

2016 USAMO (Problems • Resources)
Preceded by
Problem 2 		Followed by
Problem 4
1 • 2 • 3 • 4 • 5 • 6
All USAMO Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2016_USAMO_Problems/Problem_3&oldid=179212"