Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2016 USAMO Problems/Problem 3"

(→‎Solution)
(→‎Solution)
Line 11: Line 11:
  
 
{{MAA Notice}}
 
{{MAA Notice}}
 +
 +
==Solution 2==
 +
[[File:2016 USAMO 3a.png|300px|right]]
 +
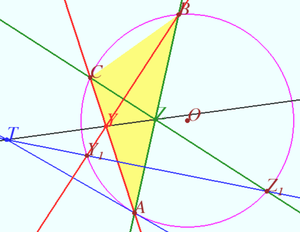
We find point <math>T</math> on line <math>YZ,</math> we prove that <math>TY \perp OI_A</math> and state that <math>P</math> is the point <math>X(24)</math> from ENCYCLOPEDIA OF TRIANGLE, therefore <math>P \in OI_A.</math>
 +
 +
Let <math>\omega</math> be circumcircle of <math>\triangle ABC</math> centered at <math>O.</math>
 +
Let <math>Y_1,</math> and <math>Z_1</math> be crosspoints of <math>\omega</math> and <math>BY,</math> and <math>CZ,</math> respectively.
 +
Let <math>T</math> be crosspoint of <math>YZ</math> and <math>Y_1 Z_1.</math>
 +
In accordance the Pascal theorem for pentagon <math>AZ_1BCY_1,</math> <math>AT</math> is tangent to <math>\omega</math> at <math>A.</math>
  
 
==See also==
 
==See also==
 
{{USAMO newbox|year=2016|num-b=2|num-a=4}}
 
{{USAMO newbox|year=2016|num-b=2|num-a=4}}

Revision as of 14:32, 2 October 2022

Problem

Let $\triangle ABC$ be an acute triangle, and let $I_B, I_C,$ and $O$ denote its $B$-excenter, $C$-excenter, and circumcenter, respectively. Points $E$ and $Y$ are selected on $\overline{AC}$ such that $\angle ABY = \angle CBY$ and $\overline{BE}\perp\overline{AC}.$ Similarly, points $F$ and $Z$ are selected on $\overline{AB}$ such that $\angle ACZ = \angle BCZ$ and $\overline{CF}\perp\overline{AB}.$

Lines $I_B F$ and $I_C E$ meet at $P.$ Prove that $\overline{PO}$ and $\overline{YZ}$ are perpendicular.

Solution

This problem can be proved in the following two steps.

1. Let $I_A$ be the $A$-excenter, then $I_A,O,$ and $P$ are colinear. This can be proved by the Trigonometric Form of Ceva's Theorem for $\triangle I_AI_BI_C.$

2. Show that $I_AY^2-I_AZ^2=OY^2-OZ^2,$ which implies $\overline{OI_A}\perp\overline{YZ}.$ This can be proved by multiple applications of the Pythagorean Thm.

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Solution 2

2016 USAMO 3a.png

We find point $T$ on line $YZ,$ we prove that $TY \perp OI_A$ and state that $P$ is the point $X(24)$ from ENCYCLOPEDIA OF TRIANGLE, therefore $P \in OI_A.$

Let $\omega$ be circumcircle of $\triangle ABC$ centered at $O.$ Let $Y_1,$ and $Z_1$ be crosspoints of $\omega$ and $BY,$ and $CZ,$ respectively. Let $T$ be crosspoint of $YZ$ and $Y_1 Z_1.$ In accordance the Pascal theorem for pentagon $AZ_1BCY_1,$ $AT$ is tangent to $\omega$ at $A.$

See also

2016 USAMO (Problems • Resources)
Preceded by
Problem 2 		Followed by
Problem 4
1 • 2 • 3 • 4 • 5 • 6
All USAMO Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2016_USAMO_Problems/Problem_3&oldid=178631"