Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 USAMO Problems/Problem 6"
(→‎Solution)
Line 3: Line 3:
  
 
==Solution==
 
==Solution==
 +
[[File:2021 USAMO 6b.png|430px|right]]
 
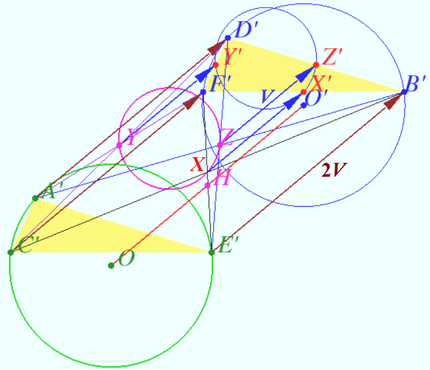
We construct two equal triangles, prove that triangle <math>XYZ</math> is the medial triangle of both this triangles, use property of medial triangle and prove that circumcenters of constructed triangles coincide with given circumcenters.
 
We construct two equal triangles, prove that triangle <math>XYZ</math> is the medial triangle of both this triangles, use property of medial triangle and prove that circumcenters of constructed triangles coincide with given circumcenters.
 +
 +
Denote <math>A' =  C + E – D, B' = D + F – E, C' =  A+ E – F,</math>
 +
<math>D' =  F+ B – A, E' =  A + C – B, F' =  B+ D – C.</math>
 +
Then <math>A' – D'  =  C + E – D –  ( F+ B – A) = (A + C + E ) – (B+ D + F).</math>
 +
Denote  <math>D' – A' = 2\vec V.</math>
 +
 +
Symilarly we get <math>B' – E' = F' – C' =  D' – A'  \implies</math>
 +
<math>\triangle ACE = \triangle BDF,</math> and the translation vector is <math>2\vec {V.}</math>
 +
<math>X = \frac {A+D}{2} =  \frac { (A+ E – F) + (D + F – E)}{2} =  \frac {C' + B'}{2} = \frac {E' + F'}{2},</math>
 +
 +
so <math>X</math> is midpoint of <math>AD, B'C',</math> and <math>E'F'.</math> Symilarly <math>Y</math> is the midpoint of <math>BE, A'F',</math> and <math>C'D', Z</math> is the midpoint of <math>CF, A'B',</math> and <math>D'E'.</math>
 +
<math>Z + V =  \frac {A' + B'}{2}+ \frac {D' – A'}{2} =  \frac {B' + D'}{2} = Z'</math> is the midpoint of <math>B'D'.</math>
 +
Symilarly <math>X' = X + V</math>  is the midpoint of <math>B'F',Y'= Y + V</math>  is the midpoint of <math>D'F',</math> so <math>X'Y'Z'</math> is the medial triangle of <math>\triangle B'D'F',</math> translated on <math>– \vec {V}.</math>
 +
It is known (see diagram) that circumcenter of triangle coincite with orthocenter of the medial triangle. Therefore  orthocenter <math>H</math> of <math>\triangle XYZ</math> is circumcenter of <math>\triangle B'D'F'</math> translated on <math>– \vec {V}.</math> It is the midpoint of segment <math>OO'</math> connected circumcenters of <math>\triangle B'D'F'</math> and <math>\triangle A'C'E'.</math>

Revision as of 06:52, 15 September 2022

Problem 6

Let $ABCDEF$ be a convex hexagon satisfying $\overline{AB} \parallel \overline{DE}$, $\overline{BC} \parallel \overline{EF}$, $\overline{CD} \parallel \overline{FA}$, and\[AB \cdot DE = BC \cdot EF = CD \cdot FA.\]Let $X$, $Y$, and $Z$ be the midpoints of $\overline{AD}$, $\overline{BE}$, and $\overline{CF}$. Prove that the circumcenter of $\triangle ACE$, the circumcenter of $\triangle BDF$, and the orthocenter of $\triangle XYZ$ are collinear.

Solution

2021 USAMO 6b.png

We construct two equal triangles, prove that triangle $XYZ$ is the medial triangle of both this triangles, use property of medial triangle and prove that circumcenters of constructed triangles coincide with given circumcenters.

Denote $A' = C + E – D, B' = D + F – E, C' = A+ E – F,$ $D' = F+ B – A, E' = A + C – B, F' = B+ D – C.$ Then $A' – D' = C + E – D – ( F+ B – A) = (A + C + E ) – (B+ D + F).$ Denote $D' – A' = 2\vec V.$

Symilarly we get $B' – E' = F' – C' = D' – A' \implies$ $\triangle ACE = \triangle BDF,$ and the translation vector is $2\vec {V.}$ $X = \frac {A+D}{2} = \frac { (A+ E – F) + (D + F – E)}{2} = \frac {C' + B'}{2} = \frac {E' + F'}{2},$

so $X$ is midpoint of $AD, B'C',$ and $E'F'.$ Symilarly $Y$ is the midpoint of $BE, A'F',$ and $C'D', Z$ is the midpoint of $CF, A'B',$ and $D'E'.$ $Z + V = \frac {A' + B'}{2}+ \frac {D' – A'}{2} = \frac {B' + D'}{2} = Z'$ is the midpoint of $B'D'.$ Symilarly $X' = X + V$ is the midpoint of $B'F',Y'= Y + V$ is the midpoint of $D'F',$ so $X'Y'Z'$ is the medial triangle of $\triangle B'D'F',$ translated on $– \vec {V}.$ It is known (see diagram) that circumcenter of triangle coincite with orthocenter of the medial triangle. Therefore orthocenter $H$ of $\triangle XYZ$ is circumcenter of $\triangle B'D'F'$ translated on $– \vec {V}.$ It is the midpoint of segment $OO'$ connected circumcenters of $\triangle B'D'F'$ and $\triangle A'C'E'.$

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_USAMO_Problems/Problem_6&oldid=178219"