Difference between revisions of "2021 USAMO Problems/Problem 1"
(→Solution) |
|||
| Line 2: | Line 2: | ||
==Solution== | ==Solution== | ||
| − | + | [[File:2021 USAMO 1.png|400px|right]] | |
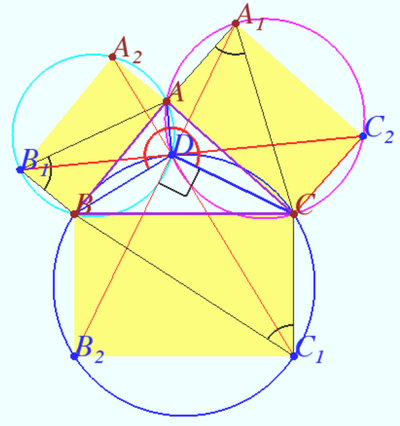
Let <math>D</math> be the second point of intersection of the circles <math>AB_1B</math> and <math>AA_1C.</math> Then | Let <math>D</math> be the second point of intersection of the circles <math>AB_1B</math> and <math>AA_1C.</math> Then | ||
<cmath>\angle ADB = 180^\circ – \angle AB_1B,\angle ADC = 180^\circ – \angle AA_1C \implies</cmath> | <cmath>\angle ADB = 180^\circ – \angle AB_1B,\angle ADC = 180^\circ – \angle AA_1C \implies</cmath> | ||
| − | <cmath>\angle BDC = 360^\circ – \angle ADB – \angle ADC = 360^\circ – (180^\circ – \angle AB_1B) – (180^\circ – \angle AA_1C) =</cmath> | + | <cmath>\angle BDC = 360^\circ – \angle ADB – \angle ADC =</cmath> |
| + | <cmath>= 360^\circ – (180^\circ – \angle AB_1B) – (180^\circ – \angle AA_1C) =</cmath> | ||
<cmath>=\angle AB_1B + \angle AA_1C \implies \angle BDC + \angle BC_1C = 180^\circ \implies</cmath> | <cmath>=\angle AB_1B + \angle AA_1C \implies \angle BDC + \angle BC_1C = 180^\circ \implies</cmath> | ||
<math>BDCC_1B_2</math> is cyclic with diameters <math>BC_1</math> and <math>CB_2 \implies \angle CDB_2 = 90^\circ.</math> | <math>BDCC_1B_2</math> is cyclic with diameters <math>BC_1</math> and <math>CB_2 \implies \angle CDB_2 = 90^\circ.</math> | ||
| + | Similarly, <math>\angle CDA_1 = 90^\circ \implies</math> points <math>A_1, D,</math> and <math>B_2</math> are collinear. | ||
| + | |||
| + | Similarly, triples of points <math>A_2, D, C_1</math> and <math>C_2, D, B_1</math> are collinear. | ||
| + | |||
| + | (After USAMO 2021 Solution Notes – Evan Chen) | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
Revision as of 06:27, 15 September 2022
Rectangles ![]()
![]() and
and ![]() are erected outside an acute triangle
are erected outside an acute triangle ![]() Suppose that
Suppose that![]() Prove that lines
Prove that lines ![]()
![]() and
and ![]() are concurrent.
are concurrent.
Solution
Let ![]() be the second point of intersection of the circles
be the second point of intersection of the circles ![]() and
and ![]() Then
Then
![]()
![]()
![]()
![]()
![]() is cyclic with diameters
is cyclic with diameters ![]() and
and ![]() Similarly,
Similarly, ![]() points
points ![]() and
and ![]() are collinear.
are collinear.
Similarly, triples of points ![]() and
and ![]() are collinear.
are collinear.
(After USAMO 2021 Solution Notes – Evan Chen)
vladimir.shelomovskii@gmail.com, vvsss