Difference between revisions of "2018 IMO Problems/Problem 6"
(→Solution) |
(→Solution) |
||
| Line 21: | Line 21: | ||
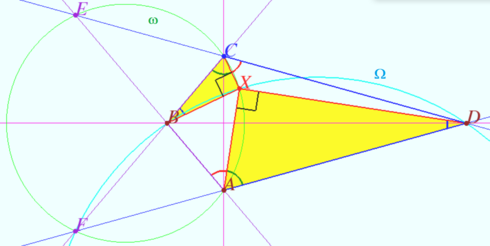
Let <math>X_0</math> be the point of intersection of the circles <math>\omega</math> and <math>\Omega.</math> | Let <math>X_0</math> be the point of intersection of the circles <math>\omega</math> and <math>\Omega.</math> | ||
| − | Quadrilateral <math>AX_0CF</math> is cyclic <math>\implies</math> <cmath>\angle X_0AB = \frac {1}{2}\overset{\Large\frown} {X_0CE} = \frac {1}{2} (360^\circ -\overset{\Large\frown} { | + | Quadrilateral <math>AX_0CF</math> is cyclic <math>\implies</math> <cmath>\angle X_0AB = \frac {1}{2}\overset{\Large\frown} {X_0CE} = \frac {1}{2} (360^\circ -\overset{\Large\frown} {X_0AE}) = 180^\circ - \angle X_0CE = \angle X_0CD.</cmath> |
Analogically, quadrangle <math>DX_0BF</math> is cyclic <math>\implies \angle X_0BC = \angle X_0DA</math>. | Analogically, quadrangle <math>DX_0BF</math> is cyclic <math>\implies \angle X_0BC = \angle X_0DA</math>. | ||
| − | This means that point <math>X_0</math> coincides with the point <math>X</math> | + | This means that point <math>X_0</math> coincides with the point <math>X</math>. |
| − | <math>\angle FCX = \angle BCX = \frac {1}{2} \overset{\Large\frown} {XAF}</math> of <math>\omega.</math> | + | <math>\hspace{10mm} \angle FCX = \angle BCX = \frac {1}{2} \overset{\Large\frown} {XAF}</math> of <math>\omega.</math> |
| − | |||
| − | |||
| − | + | <math>\hspace{10mm} \angle CBX = \angle XDA = \frac {1}{2} \overset{\Large\frown} {XBF}</math> of <math>\Omega.</math> | |
| − | + | The sum <math>\overset{\Large\frown} {XAF} + \overset{\Large\frown} {XBF} = 180^\circ</math> <i><b>(Claim 3)</b></i> <math>\implies</math> | |
| + | |||
| + | <math>\angle XCB + \angle XBC = 90^\circ \implies \angle CXB = 90^\circ.</math> | ||
Similarly, <math>\angle AXD = 90^\circ \implies \angle BXA + \angle DXC = 180^\circ.</math> | Similarly, <math>\angle AXD = 90^\circ \implies \angle BXA + \angle DXC = 180^\circ.</math> | ||
Revision as of 05:43, 19 August 2022
A convex quadrilateral ![]() satisfies
satisfies ![]() Point
Point ![]() lies inside
lies inside
![]() so that
so that
![]() and
and ![]() Prove that
Prove that ![]()
Solution
Special case
We construct point ![]() and prove that
and prove that ![]() coincides with the point
coincides with the point ![]()
Let ![]() and
and ![]()
Let ![]() and
and ![]() be the intersection points of
be the intersection points of ![]() and
and ![]() and
and ![]() and
and ![]() respectively.
respectively.
The points ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() (Claim 1).
(Claim 1).
The circle ![]() is orthogonal to the circle
is orthogonal to the circle ![]() (Claim 2).
(Claim 2).
Let ![]() be the point of intersection of the circles
be the point of intersection of the circles ![]() and
and ![]() Quadrilateral
Quadrilateral ![]() is cyclic
is cyclic ![]()
![]()
Analogically, quadrangle ![]() is cyclic
is cyclic ![]() .
.
This means that point ![]() coincides with the point
coincides with the point ![]() .
.
![]() of
of ![]()
![]() of
of ![]()
The sum ![]() (Claim 3)
(Claim 3) ![]()
![]()
Similarly, ![]()
Claim 1 Let ![]() and
and ![]() be arbitrary points on a circle
be arbitrary points on a circle ![]() be the middle perpendicular to the segment
be the middle perpendicular to the segment ![]() Then the straight lines
Then the straight lines ![]() and
and ![]() intersect
intersect ![]() at the points
at the points ![]() and
and ![]() symmetric with respect to
symmetric with respect to ![]()
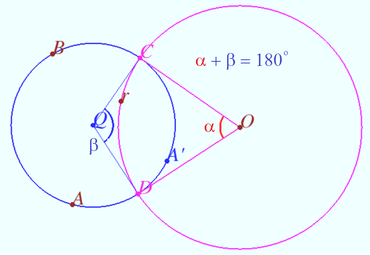
Claim 2 Let points ![]() and
and ![]() be symmetric with respect to the circle
be symmetric with respect to the circle ![]() Then any circle
Then any circle ![]() passing through these points is orthogonal to
passing through these points is orthogonal to ![]()
Claim 3 The sum of the arcs between the points of intersection of two perpendicular circles is ![]() In the figure they are a blue and red arcs
In the figure they are a blue and red arcs ![]()
Common case
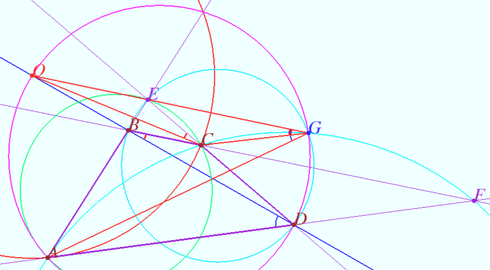
Denote by ![]() the intersection point of the midpoint perpendicular of the segment
the intersection point of the midpoint perpendicular of the segment ![]() and the line
and the line ![]() Let
Let ![]() be a circle (red) with center
be a circle (red) with center ![]() and radius
and radius ![]()
The points ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() (Claim 1).
(Claim 1).
The circles ![]() and
and ![]() are orthogonal to the circle
are orthogonal to the circle ![]() (Claim 2).
(Claim 2).
Circles ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() (Lemma).
(Lemma).