Difference between revisions of "2007 AIME I Problems/Problem 15"
(+ solution) |
Jeffersonj (talk | contribs) m |
||
| (8 intermediate revisions by 4 users not shown) | |||
| Line 7: | Line 7: | ||
Denote the length of a side of the triangle <math>x</math>, and of <math>\overline{AE}</math> as <math>y</math>. The area of the entire equilateral triangle is <math>\frac{x^2\sqrt{3}}{4}</math>. Add up the areas of the triangles using the <math>\frac{1}{2}ab\sin C</math> formula (notice that for the three outside triangles, <math>\sin 60 = \frac{\sqrt{3}}{2}</math>): <math>\frac{x^2\sqrt{3}}{4} = \frac{\sqrt{3}}{4}(5 \cdot y + (x - 2)(x - 5) + 2(x - y)) + 14\sqrt{3}</math>. This simplifies to <math>\frac{x^2\sqrt{3}}{4} = \frac{\sqrt{3}}{4}(5y + x^2 - 7x + 10 + 2x - 2y + 56)</math>. Some terms will cancel out, leaving <math>y = \frac{5}{3}x - 22</math>. | Denote the length of a side of the triangle <math>x</math>, and of <math>\overline{AE}</math> as <math>y</math>. The area of the entire equilateral triangle is <math>\frac{x^2\sqrt{3}}{4}</math>. Add up the areas of the triangles using the <math>\frac{1}{2}ab\sin C</math> formula (notice that for the three outside triangles, <math>\sin 60 = \frac{\sqrt{3}}{2}</math>): <math>\frac{x^2\sqrt{3}}{4} = \frac{\sqrt{3}}{4}(5 \cdot y + (x - 2)(x - 5) + 2(x - y)) + 14\sqrt{3}</math>. This simplifies to <math>\frac{x^2\sqrt{3}}{4} = \frac{\sqrt{3}}{4}(5y + x^2 - 7x + 10 + 2x - 2y + 56)</math>. Some terms will cancel out, leaving <math>y = \frac{5}{3}x - 22</math>. | ||
| − | <math>\angle FEC</math> is an [[ | + | <math>\angle FEC</math> is an [[exterior angle]] to <math>\triangle AEF</math>, from which we find that <math>60 + \angle CED = 60 + \angle AFE</math>, so <math>\angle CED = \angle AFE</math>. Similarly, we find that <math>\angle EDC = \angle AEF</math>. Thus, <math>\triangle AEF \sim \triangle CDE</math>. Setting up a [[ratio]] of sides, we get that <math>\frac{5}{x-y} = \frac{y}{2}</math>. Using the previous relationship between <math>x</math> and <math>y</math>, we can solve for <math>x</math>. |
<div style="text-align:center;"> | <div style="text-align:center;"> | ||
| − | <math> | + | <math>xy - y^2 = 10</math> |
<math>\frac{5}{3}x^2 - 22x - \left(\frac{5}{3}x - 22\right)^2 - 10 = 0</math> | <math>\frac{5}{3}x^2 - 22x - \left(\frac{5}{3}x - 22\right)^2 - 10 = 0</math> | ||
| Line 19: | Line 19: | ||
</div> | </div> | ||
| − | Use the [[quadratic formula]], though we only need the root of the [[discriminant]]. This is <math>\sqrt{(7 \cdot 66)^2 - 4 \cdot 10 \cdot (66^2 + 90)} = \sqrt{49 \cdot 66^2 - 40 \cdot 66^2 - 4 \cdot 9 \cdot 100}</math><math> = \sqrt{9 \cdot 4 \cdot 33^2 - 9 \cdot 4 \cdot 100} = 6\sqrt{33^2 - 100}</math>. The answer is <math>989</math>. | + | Use the [[quadratic formula]], though we only need the root of the [[discriminant]]. This is <math>\sqrt{(7 \cdot 66)^2 - 4 \cdot 10 \cdot (66^2 + 90)} = \sqrt{49 \cdot 66^2 - 40 \cdot 66^2 - 4 \cdot 9 \cdot 100}</math><math> = \sqrt{9 \cdot 4 \cdot 33^2 - 9 \cdot 4 \cdot 100} = 6\sqrt{33^2 - 100}</math>. The answer is <math>\boxed{989}</math>. |
| + | |||
| + | ==Solution 2== | ||
| + | First of all, assume <math>EC=x,BD=m, ED=a, EF=b</math>, then we can find <math>BF=m-3, AE=2+m-x</math> | ||
| + | It is not hard to find <math>ab*sin60^{\circ}*\frac{1}{2}=14\sqrt{3}, ab=56</math>, we apply LOC on <math>\triangle{DEF}, \triangle{BFD}</math>, getting that <math>(m-3)^2+m^2-m(m-3)=a^2+b^2-ab</math>, leads to <math>a^2+b^2=m^2-3m+65</math> | ||
| + | Apply LOC on <math>\triangle{CED}, \triangle{AEF}</math> separately, getting <math>4+x^2-2x=a^2; 25+(2+m-x)^2-5(2+m-x)=b^2.</math> Add those terms together and use the equality <math>a^2+b^2=m^2-3m+65</math>, we can find: | ||
| + | <math>2x^2-(2m+1)x+2m-42=0</math> | ||
| + | |||
| + | According to basic angle chasing, <math>\angle{A}=\angle{C}; \angle{AFE}=\angle{CED}</math>, so <math>\triangle{AFE}\sim \triangle{CED}</math>, the ratio makes <math>\frac{5}{x}=\frac{2+m-x}{2}</math>, getting that <math>x^2-(2+m)x+10=0</math> | ||
| + | Now we have two equations with <math>m</math>, and <math>x</math> values for both equations must be the same, so we can solve for <math>x</math> in two equations. | ||
| + | <math>x=\frac{2m+1 \pm \sqrt{4m^2+4m+1-16m+336}}{4}; x=\frac{4+2m \pm \sqrt{4m^2+16m-144}}{4}</math>, then we can just use positive sign to solve, simplifies to <math>3+\sqrt{4m^2+16m-144}=\sqrt{4m^2-12m+337}</math>, getting <math>m=\frac{211-3\sqrt{989}}{10}</math>, since the triangle is equilateral, <math>AB=BC=2+m=\frac{231-3\sqrt{989}}{10}</math>, and the desired answer is <math>\boxed{989}</math> | ||
| + | |||
| + | ~bluesoul | ||
== See also == | == See also == | ||
| Line 25: | Line 37: | ||
[[Category:Intermediate Geometry Problems]] | [[Category:Intermediate Geometry Problems]] | ||
| + | {{MAA Notice}} | ||
Latest revision as of 21:14, 6 August 2022
Contents
Problem
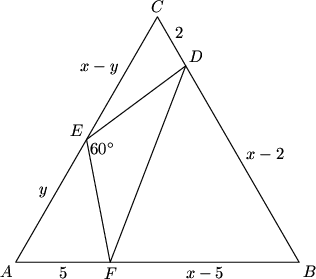
Let ![]() be an equilateral triangle, and let
be an equilateral triangle, and let ![]() and
and ![]() be points on sides
be points on sides ![]() and
and ![]() , respectively, with
, respectively, with ![]() and
and ![]() . Point
. Point ![]() lies on side
lies on side ![]() such that angle
such that angle ![]() . The area of triangle
. The area of triangle ![]() is
is ![]() . The two possible values of the length of side
. The two possible values of the length of side ![]() are
are ![]() , where
, where ![]() and
and ![]() are rational, and
are rational, and ![]() is an integer not divisible by the square of a prime. Find
is an integer not divisible by the square of a prime. Find ![]() .
.
Solution
Denote the length of a side of the triangle ![]() , and of
, and of ![]() as
as ![]() . The area of the entire equilateral triangle is
. The area of the entire equilateral triangle is ![]() . Add up the areas of the triangles using the
. Add up the areas of the triangles using the ![]() formula (notice that for the three outside triangles,
formula (notice that for the three outside triangles, ![]() ):
): ![]() . This simplifies to
. This simplifies to ![]() . Some terms will cancel out, leaving
. Some terms will cancel out, leaving ![]() .
.
![]() is an exterior angle to
is an exterior angle to ![]() , from which we find that
, from which we find that ![]() , so
, so ![]() . Similarly, we find that
. Similarly, we find that ![]() . Thus,
. Thus, ![]() . Setting up a ratio of sides, we get that
. Setting up a ratio of sides, we get that ![]() . Using the previous relationship between
. Using the previous relationship between ![]() and
and ![]() , we can solve for
, we can solve for ![]() .
.
![]()
![]()
![]()
![]()
Use the quadratic formula, though we only need the root of the discriminant. This is ![]()
![]() . The answer is
. The answer is ![]() .
.
Solution 2
First of all, assume ![]() , then we can find
, then we can find ![]() It is not hard to find
It is not hard to find ![]() , we apply LOC on
, we apply LOC on ![]() , getting that
, getting that ![]() , leads to
, leads to ![]() Apply LOC on
Apply LOC on ![]() separately, getting
separately, getting ![]() Add those terms together and use the equality
Add those terms together and use the equality ![]() , we can find:
, we can find:
![]()
According to basic angle chasing, ![]() , so
, so ![]() , the ratio makes
, the ratio makes ![]() , getting that
, getting that ![]() Now we have two equations with
Now we have two equations with ![]() , and
, and ![]() values for both equations must be the same, so we can solve for
values for both equations must be the same, so we can solve for ![]() in two equations.
in two equations.
![]() , then we can just use positive sign to solve, simplifies to
, then we can just use positive sign to solve, simplifies to ![]() , getting
, getting ![]() , since the triangle is equilateral,
, since the triangle is equilateral, ![]() , and the desired answer is
, and the desired answer is ![]()
~bluesoul
See also
| 2007 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.