Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2020 AIME II Problems/Problem 15"

(→‎Solution 4 (Similarity and median))
(→‎Solution 4 (Similarity and median))
Line 73: Line 73:
  
 
==Solution 4 (Similarity and median)==
 
==Solution 4 (Similarity and median)==
 +
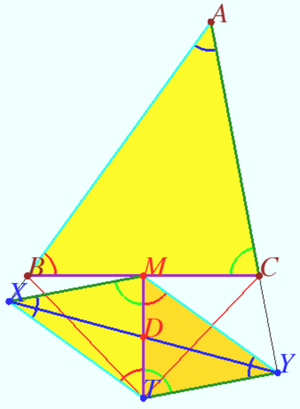
[[File:2020 AIME II 15a.png|300px|right]]
 +
Using the <i><b>Lemma</b></i> (below) we get <math>\triangle ABC \sim \triangle XTM \sim \triangle YMT.</math>
 +
 +
Corresponding sides of similar <math>\triangle XTM \sim \triangle YMT</math> is <math>MT,</math> so
 +
 +
<math>\triangle XTM = \triangle YMT \implies MY = XT, MX = TY \implies XMYT</math> – parallelogram.
 +
 +
<cmath>4 TD^2 = MT^2 = \sqrt{BT^2 - BM^2}  =\sqrt{153}.</cmath>
 +
The formula for median <math>DT</math> of triangle <math>XYT</math> is
 +
<cmath>2 DT^2 = XT^2 + TY^2 – \frac{XY^2}{2},</cmath>
 +
<cmath>3 \cdot XY^2 = 2XT^2 + 2TY^2 + 2XY^2 –  4 DT^2,</cmath>
 +
<cmath>3 \cdot XY^2  = 2 \cdot 1143-153 = 2151 \implies XY^2 = \boxed{717}. </cmath>
 +
 +
 
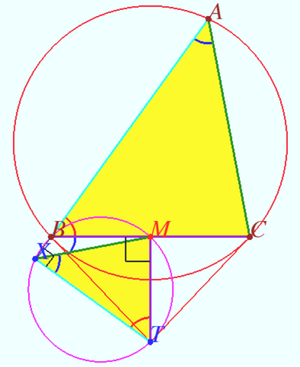
[[File:2020 AIME II 15.png|300px|right]]
 
[[File:2020 AIME II 15.png|300px|right]]
 
<i><b>Lemma</b></i>
 
<i><b>Lemma</b></i>
Line 86: Line 100:
 
<math>\angle CBT = \angle BAC = \frac {\overset{\Large\frown} {BC}}{ 2} \implies \triangle ABC \sim \triangle XTM.</math>
 
<math>\angle CBT = \angle BAC = \frac {\overset{\Large\frown} {BC}}{ 2} \implies \triangle ABC \sim \triangle XTM.</math>
  
−
<i><b>Solution</b></i>
 
−
[[File:2020 AIME II 15a.png|300px|right]]
 
−
<math>\triangle ABC \sim \triangle XTM \sim \triangle YMT.</math>
 
−
 
−
Corresponding sides of similar <math>\triangle XTM \sim \triangle YMT</math> is <math>MT,</math> so
 
  
−
<math>\triangle XTM = \triangle YMT \implies MY = XT, MX = TY \implies XMYT</math> – parallelogram.
 
−
 
−
<cmath>4 TD^2 = MT^2 = \sqrt{BT^2 - BM^2}  =\sqrt{153}.</cmath>
 
−
The formula for median <math>DT</math> of triangle <math>XYT</math> is
 
−
<cmath>2 DT^2 = XT^2 + TY^2 – \frac{XY^2}{2},</cmath>
 
−
<cmath>3 \cdot XY^2 = 2XT^2 + 2TY^2 + 2XY^2 –  4 DT^2,</cmath>
 
−
<cmath>3 \cdot XY^2  = 2 \cdot 1143-153 = 2151 \implies XY^2 = \boxed{717}. </cmath>
 
  
−
~vvsss, www.deoma-cmd.ru
+
'''Shelomovskii, vvsss, www.deoma-cmd.ru'''
  
 
==See Also==
 
==See Also==

Revision as of 14:55, 17 June 2022

Problem

Let $\triangle ABC$ be an acute scalene triangle with circumcircle $\omega$. The tangents to $\omega$ at $B$ and $C$ intersect at $T$. Let $X$ and $Y$ be the projections of $T$ onto lines $AB$ and $AC$, respectively. Suppose $BT = CT = 16$, $BC = 22$, and $TX^2 + TY^2 + XY^2 = 1143$. Find $XY^2$.

Solution

Assume $O$ to be the center of triangle $ABC$, $OT$ cross $BC$ at $M$, link $XM$, $YM$. Let $P$ be the middle point of $BT$ and $Q$ be the middle point of $CT$, so we have $MT=3\sqrt{15}$. Since $\angle A=\angle CBT=\angle BCT$, we have $\cos A=\frac{11}{16}$. Notice that $\angle XTY=180^{\circ}-A$, so $\cos XYT=-\cos A$, and this gives us $1143-2XY^2=\frac{-11}{8}XT\cdot YT$. Since $TM$ is perpendicular to $BC$, $BXTM$ and $CYTM$ cocycle (respectively), so $\theta_1=\angle ABC=\angle MTX$ and $\theta_2=\angle ACB=\angle YTM$. So $\angle XPM=2\theta_1$, so \[\frac{\frac{XM}{2}}{XP}=\sin \theta_1\], which yields $XM=2XP\sin \theta_1=BT(=CT)\sin \theta_1=TY.$ So same we have $YM=XT$. Apply Ptolemy theorem in $BXTM$ we have $16TY=11TX+3\sqrt{15}BX$, and use Pythagoras theorem we have $BX^2+XT^2=16^2$. Same in $YTMC$ and triangle $CYT$ we have $16TX=11TY+3\sqrt{15}CY$ and $CY^2+YT^2=16^2$. Solve this for $XT$ and $TY$ and submit into the equation about $\cos XYT$, we can obtain the result $XY^2=\boxed{717}$.

(Notice that $MXTY$ is a parallelogram, which is an important theorem in Olympiad, and there are some other ways of computation under this observation.)

-Fanyuchen20020715

Solution 2 (Official MAA)

Let $M$ denote the midpoint of $\overline{BC}$. The critical claim is that $M$ is the orthocenter of $\triangle AXY$, which has the circle with diameter $\overline{AT}$ as its circumcircle. To see this, note that because $\angle BXT = \angle BMT = 90^\circ$, the quadrilateral $MBXT$ is cyclic, it follows that \[\angle MXA = \angle MXB = \angle MTB = 90^\circ - \angle TBM = 90^\circ - \angle A,\] implying that $\overline{MX} \perp \overline{AC}$. Similarly, $\overline{MY} \perp \overline{AB}$. In particular, $MXTY$ is a parallelogram. [asy] defaultpen(fontsize(8pt)); unitsize(0.8cm); pair A = (0,0); pair B = (-1.26,-4.43); pair C = (-1.26+3.89, -4.43); pair M = (B+C)/2; pair O = circumcenter(A,B,C); pair T = (0.68, -6.49); pair X = foot(T,A,B); pair Y = foot(T,A,C); path omega = circumcircle(A,B,C); real rad = circumradius(A,B,C); filldraw(A--B--C--cycle, rgb(0/255,0/255,255/255)); label("$\omega$", O + rad*dir(45), SW); filldraw(T--Y--M--X--cycle, rgb(0/255,255/255,0/255)); draw(M--T); draw(X--Y); draw(B--T--C); draw(A--X--Y--cycle); draw(omega); dot("$X$", X, W); dot("$Y$", Y, E); dot("$O$", O, W); dot("$T$", T, S); dot("$A$", A, N); dot("$B$", B, W); dot("$C$", C, E); dot("$M$", M, N); [/asy] Hence, by the Parallelogram Law, \[TM^2 + XY^2 = 2(TX^2 + TY^2) = 2(1143-XY^2).\] But $TM^2 = TB^2 - BM^2 = 16^2 - 11^2 = 135$. Therefore \[XY^2 = \frac13(2 \cdot 1143-135) = 717.\]

Solution 3 (Law of Cosines)

Let $H$ be the orthocenter of $\triangle AXY$.

Lemma 1: $H$ is the midpoint of $BC$.

Proof: Let $H'$ be the midpoint of $BC$, and observe that $XBH'T$ and $TH'CY$ are cyclical. Define $H'Y \cap BA=E$ and $H'X \cap AC=F$, then note that: \[\angle H'BT=\angle H'CT=\angle H'XT=\angle H'YT=\angle A.\] That implies that $\angle H'XB=\angle H'YC=90^\circ-\angle A$, $\angle CH'Y=\angle EH'B=90^\circ-\angle B$, and $\angle BH'Y=\angle FH'C=90^\circ-\angle C$. Thus $YH'\perp AX$ and $XH' \perp AY$; $H'$ is indeed the same as $H$, and we have proved lemma 1.

Since $AXTY$ is cyclical, $\angle XTY=\angle XHY$ and this implies that $XHYT$ is a paralelogram. By the Law of Cosines: \[XY^2=XT^2+TY^2+2(XT)(TY)\cdot \cos(\angle A)\] \[XY^2=XH^2+HY^2+2(XH)(HY) \cdot \cos(\angle A)\] \[HT^2=HX^2+XT^2-2(HX)(XT) \cdot \cos(\angle A)\] \[HT^2=HY^2+YT^2-2(HY)(YT) \cdot \cos(\angle A).\] We add all these equations to get: \[HT^2+XY^2=2(XT^2+TY^2) \qquad (1).\] We have that $BH=HC=11$ and $BT=TC=16$ using our midpoints. Note that $HT \perp BC$, so by the Pythagorean Theorem, it follows that $HT^2=135$. We were also given that $XT^2+TY^2=1143-XY^2$, which we multiply by $2$ to use equation $(1)$. \[2(XT^2+TY^2)=2286-2 \cdot XY^2\] Since $2(XT^2+TY^2)=2(HT^2+TY^2)=HT^2+XY^2$, we have \[135+XY^2=2286-2 \cdot XY^2\] \[3 \cdot XY^2=2151.\] Therefore, $XY^2=\boxed{717}$. ~ MathLuis

Solution 4 (Similarity and median)

2020 AIME II 15a.png

Using the Lemma (below) we get $\triangle ABC \sim \triangle XTM \sim \triangle YMT.$

Corresponding sides of similar $\triangle XTM \sim \triangle YMT$ is $MT,$ so

$\triangle XTM = \triangle YMT \implies MY = XT, MX = TY \implies XMYT$ – parallelogram.

\[4 TD^2 = MT^2 = \sqrt{BT^2 - BM^2} =\sqrt{153}.\] The formula for median $DT$ of triangle $XYT$ is \[2 DT^2 = XT^2 + TY^2 – \frac{XY^2}{2},\] \[3 \cdot XY^2 = 2XT^2 + 2TY^2 + 2XY^2 – 4 DT^2,\] \[3 \cdot XY^2 = 2 \cdot 1143-153 = 2151 \implies XY^2 = \boxed{717}.\]


2020 AIME II 15.png

Lemma

Let $\triangle ABC$ be an acute scalene triangle with circumcircle $\omega$. The tangents to $\omega$ at $B$ and $C$ intersect at $T$. Let $X$ be the projections of $T$ onto line $AB$. Let M be midpoint BC. Then triangle ABC is similar to triangle XTM.

Proof

$\angle BXT = \angle BMT = 90^o \implies$ the quadrilateral $MBXT$ is cyclic.

$BM \perp MT, TX \perp AB \implies \angle MTX = \angle MBA.$

$\angle CBT = \angle BAC = \frac {\overset{\Large\frown} {BC}}{ 2} \implies \triangle ABC \sim \triangle XTM.$


Shelomovskii, vvsss, www.deoma-cmd.ru

See Also

2020 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 14 		Followed by
Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2020_AIME_II_Problems/Problem_15&oldid=174982"