Difference between revisions of "2022 AIME I Problems/Problem 11"

Revision as of 10:52, 31 May 2022

Problem

Let $ABCD$ be a parallelogram with $\angle BAD < 90^{\circ}$ . A circle tangent to sides $\overline{DA}$ , $\overline{AB}$ , and $\overline{BC}$ intersects diagonal $\overline{AC}$ at points $P$ and $Q$ with $AP < AQ$ , as shown. Suppose that $AP = 3$ , $PQ = 9$ , and $QC = 16$ . Then the area of $ABCD$ can be expressed in the form $m\sqrt n$ , where $m$ and $n$ are positive integers, and $n$ is not divisible by the square of any prime. Find $m+n$ .

$[asy] defaultpen(linewidth(0.6)+fontsize(11)); size(8cm); pair A,B,C,D,P,Q; A=(0,0); label("$A$", A, SW); B=(6,15); label("$B$", B, NW); C=(30,15); label("$C$", C, NE); D=(24,0); label("$D$", D, SE); P=(5.2,2.6); label("$P$", (5.8,2.6), N); Q=(18.3,9.1); label("$Q$", (18.1,9.7), W); draw(A--B--C--D--cycle); draw(C--A); draw(Circle((10.95,7.45), 7.45)); dot(A^^B^^C^^D^^P^^Q); [/asy]$

Solution 1 (No trig)

Let's redraw the diagram, but extend some helpful lines.

$[asy] size(20cm); pair A,B,C,D,E,F,P,Q,O; A=(0,0); E = (24,15); F = (30,0); O = (10.5,7.5); label("$A$", A, SW); B=(6,15); label("$B$", B, NW); C=(30,15); label("$C$", C, NE); D=(24,0); label("$D$", D, SE); P=(5.2,2.6); label("$P$", (5.8,2.6), N); Q=(18.3,9.1); label("$Q$", (18.1,9.7), W); draw(A--B--C--D--cycle); draw(C--A); draw(Circle((10.95,7.45), 7.45)); dot(A^^B^^C^^D^^P^^Q); dot(O); label("$O$",O,W); draw((10.5,15)--(10.5,0)); draw(D--(24,15),dashed); draw(C--(30,0),dashed); draw(D--(30,0)); dot(E); dot(F); label("$3$", midpoint(A--P), S); label("$9$", midpoint(P--Q), S); label("$16$", midpoint(Q--C), S); label("$x$", (5.5,13.75), W); label("$20$", (20.25,15), N); label("$6$", (5.25,0), S); label("$6$", (1.5,3.75), W); label("$x$", (8.25,15),N); label("$14+x$", (17.25,0), S); label("$6-x$", (27,15), N); label("$6+x$", (27,7.5), W); label("$6\sqrt{3}$", (30,7.5),W); label("$T_1$", (10.5,15), N); label("$T_2$", (10.5,0), S); label("$T_3$", (4.5,11.25),W); label("$E$",E, N); label("$F$",F, S); [/asy]$

We obviously see that we must use power of a point since they've given us lengths in a circle and there are intersection points. Let $T_1, T_2, T_3$ be our tangents from the circle to the parallelogram. By the secant power of a point, the power of $A = 3 \cdot (3+9) = 36$ . Then $AT_2 = AT_3 = \sqrt{36} = 6$ . Similarly, the power of $C = 16 \cdot (16+9) = 400$ and $CT_1 = \sqrt{400} = 20$ . We let $BT_3 = BT_1 = x$ and label the diagram accordingly.

Notice that because $BC = AD, 20+x = 6+DT_2 \implies DT_2 = 14+x$ . Let $O$ be the center of the circle. Since $OT_1$ and $OT_2$ intersect $BC$ and $AD$ , respectively, at right angles, we have $T_2T_2CD$ is a right-angled trapezoid and more importantly, the diameter of the circle is the height of the triangle. Therefore, we can drop an altitude from $D$ to $BC$ and $C$ to $AD$ , and both are equal to $2r$ . Since $T_1E = T_2D$ , $20 - CE = 14+x \implies CE = 6-x$ . Since $CE = DF, DF = 6-x$ and $AF = 6+14+x+6-x = 26$ . We can now use Pythagorean theorem on $\triangle ACF$ ; we have $26^2 + (2r)^2 = (3+9+16)^2 \implies 4r^2 = 784-676 \implies 4r^2 = 108 \implies 2r = 6\sqrt{3}$ and $r^2 = 27$ .

We know that $CD = 6+x$ because $ABCD$ is a parallelogram. Using Pythagorean theorem on $\triangle CDF$ , $(6+x)^2 = (6-x)^2 + 108 \implies (6+x)^2-(6-x)^2 = 108 \implies 12 \cdot 2x = 108 \implies 2x = 9 \implies x = \frac{9}{2}$ . Therefore, base $BC = 20 + \frac{9}{2} = \frac{49}{2}$ . Thus the area of the parallelogram is the base times the height, which is $\frac{49}{2} \cdot 6\sqrt{3} = 147\sqrt{3}$ and the answer is $\boxed{150}$

~KingRavi

Solution 2

Let the circle tangent to $BC,AD,AB$ at $P,Q,M$ separately, denote that $\angle{ABC}=\angle{D}=\alpha$

Using POP, it is very clear that $PC=20,AQ=AM=6$ , let $BM=BP=x,QD=14+x$ , using LOC in $\triangle{ABP}$ , $x^2+(x+6)^2-2x(x+6)\cos\alpha=36+PQ^2$ , similarly, use LOC in $\triangle{DQC}$ , getting that $(14+x)^2+(6+x)^2-2(6+x)(14+x)\cos\alpha=400+PQ^2$ . We use the second equation to minus the first equation, getting that $28x+196-(2x+12)*14*\cos\alpha=364$ , we can get $\cos\alpha=\frac{2x-12}{2x+12}$ .

Now applying LOC in $\triangle{ADC}$ , getting $(6+x)^2+400-2(6+x)*20*\frac{2x-12}{2x+12}=(3+9+16)^2$ , solving this equation to get $x=\frac{9}{2}$ , then $\cos\alpha=-\frac{1}{7}$ , $\sin\alpha=\frac{4\sqrt{3}}{7}$ , the area is $\frac{21}{2}*\frac{49}{2}*\frac{4\sqrt{3}}{7}=147\sqrt{3}$ leads to $\boxed{150}$

~bluesoul

Solution 3

Denote by $O$ the center of the circle. Denote by $r$ the radius of the circle. Denote by $E$ , $F$ , $G$ the points that the circle meets $AB$ , $CD$ , $AD$ at, respectively.

Because the circle is tangent to $AD$ , $CB$ , $AB$ , $OE = OF = OG = r$ , $OE \perp AD$ , $OF \perp CB$ , $OG \perp AB$ .

Because $AD \parallel CB$ , $E$ , $O$ , $F$ are collinear.

Following from the power of a point, $AG^2 = AE^2 = AP \cdot AQ$ . Hence, $AG = AE = 6$ .

Following from the power of a point, $CF^2 = CQ \cdot CP$ . Hence, $CF = 20$ .

Denote $BG = x$ . Because $DG$ and $DF$ are tangents to the circle, $BF = x$ .

Because $AEFB$ is a right trapezoid, $AB^2 = EF^2 + \left( AE - BF \right)^2$ . Hence, $\left( 6 + x \right)^2 = 4 r^2 + \left( 6 - x \right)^2$ . This can be simplified as \[ 6 x = r^2 . \hspace{1cm} (1) \]

In $\triangle ACB$ , by applying the law of cosines, we have \begin{align*} AC^2 & = AB^2 + CB^2 - 2 AB \cdot CB \cos B \\ & = AB^2 + CB^2 + 2 AB \cdot CB \cos A \\ & = AB^2 + CB^2 + 2 AB \cdot CB \cdot \frac{AE - BF}{AB} \\ & = AB^2 + CB^2 + 2 CB \left( AE - BF \right) \\ & = \left( 6 + x \right)^2 + \left( 20 + x \right)^2 + 2 \left( 20 + x \right) \left( 6 - x \right) \\ & = 24 x + 676 . \end{align*}

Because $AC = AP + PQ + QC = 28$ , we get $x = \frac{9}{2}$ . Plugging this into Equation (1), we get $r = 3 \sqrt{3}$ .

Therefore, \begin{align*} {\rm Area} \ ABCD & = CB \cdot EF \\ & = \left( 20 + x \right) \cdot 2r \\ & = 147 \sqrt{3} . \end{align*}

Therefore, the answer is $147 + 3 = \boxed{\textbf{(150) }}$ .

~Steven Chen (www.professorchenedu.com)

Solution 4

Let $\omega$ be the circle, let $r$ be the radius of $\omega$ , and let the points at which $\omega$ is tangent to $AB$ , $BC$ , and $AD$ be $X$ , $Y$ , and $Z$ , respectively. Note that PoP on $A$ and $C$ with respect to $\omega$ yields $AX=6$ and $CY=20$ . We can compute the area of $ABC$ in two ways:

1. By the half-base-height formula, $[ABC]=r(20+BX)$ .

2. We can drop altitudes from the center $O$ of $\omega$ to $AB$ , $BC$ , and $AC$ , which have lengths $r$ , $r$ , and $\sqrt{r^2-81/4}$ . Thus, $[ABC]=[OAB]+[OBC]+[OAC]=r(BX+13)+14\sqrt{r^2-81/4}$ .

Equating the two expressions for $[ABC]$ and solving for $r$ yields $r=3\sqrt{3}$ .

Let $BX=BY=a$ . By the Parallelogram Law, $(a+6)^2+(a+20)^2=38^2$ . Solving for $a$ yields $a=9/2$ . Thus, $[ABCD]=2[ABC]=2r(20+a)=147\sqrt{3}$ , for a final answer of $\boxed{150}$ .

~ Leo.Euler

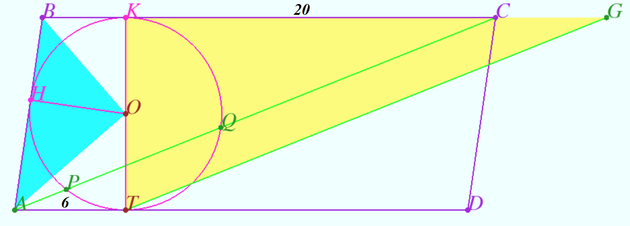
Solution 5

Let $\omega$ be the circle, let $r$ be the radius of $\omega$ , and let the points at which $\omega$ is tangent to $AB$ , $BC$ , and $AD$ be $H$ , $K$ , and $T$ , respectively. PoP on $A$ and $C$ with respect to $\omega$ yields $AT=6, CK=20.$

Let $TG = AC, TG||AT.$

In $\triangle KGT$ $KT \perp BC,$ $KT = \sqrt{GT^2 – (KC + AT)^2} = 6 \sqrt{3}=2r.$

$\angle AOB = 90^{\circ}, OH = r = \frac{KT}{2},$ $OH^2 = AH \cdot BH \implies BH = \frac {9}{2}.$

Area is $(BK + KC) \cdot KT = (BH + KC) \cdot 2r = \frac{49}{2} \cdot 6\sqrt{3} = 147 \sqrt{3} \implies 147+3 = \boxed{151}.$

~vvsss (www.deoma-cmd.ru)

Video Solution

https://www.youtube.com/watch?v=FeM_xXiJj0c&t=1s

~Steven Chen (www.professorchenedu.com)

Video Solution 2 (Mathematical Dexterity)

https://www.youtube.com/watch?v=1nDKQkr9NaU

@@ Line 164: / Line 164: @@
 Let <math>TG = AC, TG||AT.</math>
-In right <math>\triangle KGT</math>
+In  <math>\triangle KGT</math>  <math>KT \perp BC,</math>
 <math>KT = \sqrt{GT^2 – (KC + AT)^2} = 6 \sqrt{3}=2r.</math>
@@ Line 171: / Line 171: @@
 Area is <cmath>(BK + KC) \cdot KT = (BH + KC) \cdot 2r = \frac{49}{2} \cdot 6\sqrt{3} = 147 \sqrt{3} \implies 147+3 = \boxed{151}.</cmath>
+~vvsss (www.deoma-cmd.ru)
 ==Video Solution==

2022 AIME I (Problems • Answer Key • Resources)
Preceded by Problem 10	Followed by Problem 12
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search