Difference between revisions of "2021 JMPSC Invitationals Problems/Problem 12"

Latest revision as of 20:45, 22 December 2021

Problem

Rectangle $ABCD$ is drawn such that $AB=7$ and $BC=4$ . $BDEF$ is a square that contains vertex $C$ in its interior. Find $CE^2+CF^2$ .

Solution 1 (Clever Construction)

We draw a line from $E$ to point $G$ on $DC$ such that $EG \perp CD$ . We then draw a line from $F$ to point $H$ on $EG$ such that $FH \perp EG$ . Finally, we extend $BC$ to point $I$ on $FH$ such that $CI \perp FH$ .

Next, if we mark $\angle CBD$ as $x$ , we know that $\angle BDC = 90-x$ , and $\angle EDG = x$ . We repeat this, finding $\angle CBD = \angle EDG = \angle FEH = \angle BFI = x$ , so by AAS congruence, $\triangle BDC \cong \triangle DEG \cong \triangle EFH \cong \triangle FBI$ . This means $BC = DG = EH = FI = AD = 4$ , and $DC = EG = FH = BI = AB = 7$ , so $CG = GH = HI = IC = 7-4 = 3$ . We see $CF^2 = CI^2 + IF^2 = 3^2 + 4^2 = 9 + 16 = 25$ , while $CE^2 = CG^2 + GE^2 = 3^2 + 7^2 = 9 + 49 = 58$ . Thus, $CF^2 + CE^2 = 25 + 58 = \boxed{83}.$ ~Bradygho

Solution 2 (Trig)

Let $\angle DBC = \theta$ . We have $\cos(90- \theta)=\sin(\theta)=\frac{7 \sqrt{65}}{65}$ , and $\cos(\angle CDE)=\frac{4 \sqrt{65}}{65}$ . Now, Law Of cosines on $\triangle DCE$ and $\triangle BCF$ gets $CF^2=25$ and $CE^2=58$ , so $CE^2+CF^2=\boxed{83}.$ ~ Geometry285

Solution 3 (Mass points and Ptolemy)

Let $O$ be the center of square $BDEF$ . Applying moment of inertia to the system of mass points $\Sigma = {1B,1D,1E,1F}$ (which has center of mass $O$ ) gives $CB^2 + CD^2 + CE^2 + CF^2 = OB^2 + OD^2 + OE^2 + OF^2 + 4OC^2.$ Since $\triangle CBD$ is a right triangle, we may further cancel out some terms via Pythag to get $CE^2 + CF^2 = OE^2 + OF^2 + 4OC^2 = 65 + 4OC^2.$ To compute $OC$ , apply Ptolemy to cyclic quadrilateral $DOCB$ (using the fact that $\triangle BOD$ is 45-45-90) to get $OC = \tfrac{3}{\sqrt 2}$ . Thus $CE^2 + CF^2 = 65 + 4\cdot\frac 92 = 65 + 18 = \boxed{83}.$ ~djmathman

@@ Line 2: / Line 2: @@
 Rectangle <math>ABCD</math> is drawn such that <math>AB=7</math> and <math>BC=4</math>. <math>BDEF</math> is a square that contains vertex <math>C</math> in its interior. Find <math>CE^2+CF^2</math>.
-==Solution==
+==Solution 1 (Clever Construction)==
-asdf
+<center>
+[[File:Invites12.png|300px]]
+</center>
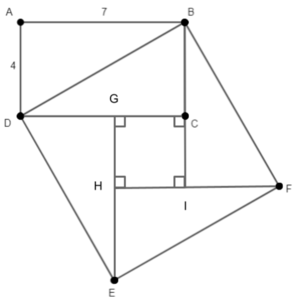
+We draw a line from <math>E</math> to point <math>G</math> on <math>DC</math> such that <math>EG \perp CD</math>. We then draw a line from <math>F</math> to point <math>H</math> on <math>EG</math> such that <math>FH \perp EG</math>. Finally, we extend <math>BC</math> to point <math>I</math> on <math>FH</math> such that <math>CI \perp FH</math>.
+Next, if we mark <math>\angle CBD</math> as <math>x</math>, we know that <math>\angle BDC = 90-x</math>, and <math>\angle EDG = x</math>. We repeat this, finding  <math>\angle CBD = \angle EDG = \angle FEH = \angle BFI = x</math>, so by AAS congruence, <math>\triangle BDC \cong \triangle DEG \cong \triangle EFH \cong \triangle FBI</math>. This means <math>BC = DG = EH = FI = AD = 4</math>, and <math>DC = EG = FH = BI = AB = 7</math>, so <math>CG = GH = HI = IC = 7-4 = 3</math>. We see <math>CF^2 = CI^2 + IF^2 = 3^2 + 4^2 = 9 + 16 = 25</math>, while <math>CE^2 = CG^2 + GE^2 = 3^2 + 7^2 = 9 + 49 = 58</math>. Thus, <math>CF^2 + CE^2 = 25 + 58 = \boxed{83}.</math> ~Bradygho
+==Solution 2 (Trig)==
+Let <math>\angle DBC = \theta</math>. We have <math>\cos(90- \theta)=\sin(\theta)=\frac{7 \sqrt{65}}{65}</math>, and <math>\cos(\angle CDE)=\frac{4 \sqrt{65}}{65}</math>. Now, Law Of cosines on <math>\triangle DCE</math> and <math>\triangle BCF</math> gets <math>CF^2=25</math> and <math>CE^2=58</math>, so <math>CE^2+CF^2=\boxed{83}.</math> ~ Geometry285
+==Solution 3 (Mass points and Ptolemy)==
+Let <math>O</math> be the center of square <math>BDEF</math>.  Applying moment of inertia to the system of mass points <math>\Sigma = {1B,1D,1E,1F}</math> (which has center of mass <math>O</math>) gives <cmath>CB^2 + CD^2 + CE^2 + CF^2 = OB^2 + OD^2 + OE^2 + OF^2 + 4OC^2.</cmath> Since <math>\triangle CBD</math> is a right triangle, we may further cancel out some terms via Pythag to get <cmath>CE^2 + CF^2 = OE^2 + OF^2 + 4OC^2 = 65 + 4OC^2.</cmath> To compute <math>OC</math>, apply Ptolemy to cyclic quadrilateral <math>DOCB</math> (using the fact that <math>\triangle BOD</math> is 45-45-90) to get <math>OC = \tfrac{3}{\sqrt 2}</math>.  Thus <cmath>CE^2 + CF^2 = 65 + 4\cdot\frac 92 = 65 + 18 = \boxed{83}.</cmath> ~djmathman
+==See also==
+#[[2021 JMPSC Invitationals Problems|Other 2021 JMPSC Invitationals Problems]]
+#[[2021 JMPSC Invitationals Answer Key|2021 JMPSC Invitationals Answer Key]]
+#[[JMPSC Problems and Solutions|All JMPSC Problems and Solutions]]
+{{JMPSC Notice}}

Page

Toolbox

Search