Difference between revisions of "2021 AMC 10A Problems/Problem 19"

Revision as of 09:42, 29 October 2021

Problem

The area of the region bounded by the graph of $x^2+y^2 = 3|x-y| + 3|x+y|$ is $m+n\pi$ , where $m$ and $n$ are integers. What is $m + n$ ?

$\textbf{(A)} ~18\qquad\textbf{(B)} ~27\qquad\textbf{(C)} ~36\qquad\textbf{(D)} ~45\qquad\textbf{(E)} ~54$

Solution 1

In order to attack this problem, we need to consider casework:

Case 1: $|x-y|=x-y, |x+y|=x+y$

Substituting and simplifying, we have $x^2-6x+y^2=0$ , i.e. $(x-3)^2+y^2=3^2$ , which gives us a circle of radius $3$ centered at $(3,0)$ .

Case 2: $|x-y|=y-x, |x+y|=x+y$

Substituting and simplifying again, we have $x^2+y^2-6y=0$ , i.e. $x^2+(y-3)^2=3^2$ . This gives us a circle of radius $3$ centered at $(0,3)$ .

Case 3: $|x-y|=x-y, |x+y|=-x-y$

Doing the same process as before, we have $x^2+y^2+6y=0$ , i.e. $x^2+(y+3)^2=3^2$ . This gives us a circle of radius $3$ centered at $(0,-3)$ .

Case 4: $|x-y|=y-x, |x+y|=-x-y$

One last time: we have $x^2+y^2+6x=0$ , i.e. $(x+3)^2+y^2=3^2$ . This gives us a circle of radius $3$ centered at $(-3,0)$ .

After combining all the cases and drawing them on the Cartesian Plane, this is what the diagram looks like:

$[asy] size(10cm); Label f; f.p=fontsize(7); xaxis(-8,8,Ticks(f, 1.0)); yaxis(-8,8,Ticks(f, 1.0)); draw(arc((-3,0),3,90,270) -- cycle, gray); draw(arc((0,3),3,0,180) -- cycle, gray); draw(arc((3,0),3,-90,90) -- cycle, gray); draw(arc((0,-3),3,-180,0) -- cycle, gray); draw((-3,3)--(3,3)--(3,-3)--(-3,-3)--cycle, grey); [/asy]$ Now, the area of the shaded region is just a square with side length $6$ with four semicircles of radius $3$ . The area is $6\cdot6+4\cdot \frac{9\pi}{2} = 36+18\pi$ . The answer is $36+18$ which is $\boxed{\textbf{(E) }54}$

Solution by Bryguy

Remark

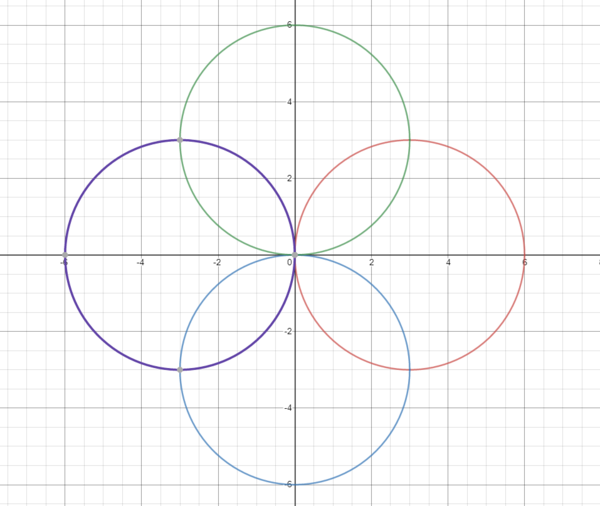
This problem asks for the area of the union of these four circles:

Solution 2 (Guessing)

Assume $y$ = $0$ . We get that $x$ = $6$ . That means that this figure must contain the points $(0,6), (6,0), (0, -6), (-6, 0)$ . Now, assume that $x$ = $y$ . We get that $x$ = $3 \sqrt 3$ . We get the points $(3,3), (3,-3), (-3, 3), (-3, -3)$ .

Since this contains $x^2 + y^2$ , assume that there are circles. Therefore, we can guess that there is a center square with area $6 \cdot 6$ = $36$ and $4$ semicircles with radius $3$ . We get $4$ semicircles with area $4.5 \pi$ , and therefore the answer is $36+18$ = $\boxed {(E)54}$

~Arcticturn

Video Solution (Using Absolute Value Properties to Graph)

https://youtu.be/EHHpB6GIGPc

~ pi_is_3.14

Video Solution by The Power Of Logic (Graphing)

https://youtu.be/-pa72wBA85Y

Video Solution by TheBeautyofMath

https://youtu.be/U6obY_kio0g

~IceMatrix

@@ Line 47: / Line 47: @@
 [[File:Image 2021-02-11 111327.png|center|600px]]
-==Solution 2==
+==Solution 2 (Guessing)==
+Assume <math>y</math> = <math>0</math>. We get that <math>x</math> = <math>6</math>. That means that this figure must contain the points <math>(0,6), (6,0), (0, -6), (-6, 0)</math>. Now, assume that <math>x</math> = <math>y</math>. We get that <math>x</math> = <math>3 \sqrt 3</math>. We get the points <math>(3,3), (3,-3), (-3, 3), (-3, -3)</math>.
+Since this contains <math>x^2 + y^2</math>, assume that there are circles. Therefore, we can guess that there is a center square with area <math>6 \cdot 6</math> = <math>36</math> and <math>4</math> semicircles with radius <math>3</math>. We get <math>4</math> semicircles with area <math>4.5 \pi</math>, and therefore the answer is <math>36+18</math> = <math>\boxed {(E)54}</math>
+~Arcticturn
 == Video Solution (Using Absolute Value Properties to Graph) ==

2021 AMC 10A (Problems • Answer Key • Resources)
Preceded by Problem 18	Followed by Problem 20
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

Page

Toolbox

Search