Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2013 AMC 10A Problems/Problem 20"

(Image)
m (→‎Solution 2)
 
(37 intermediate revisions by 14 users not shown)
Line 20: Line 20:
 
path arcrot=arc(origin,sqrt(2)/2,45+90*i,90*(i+1));
 
path arcrot=arc(origin,sqrt(2)/2,45+90*i,90*(i+1));
 
draw(arcrot);
 
draw(arcrot);
−
fill(arcrot--((sqrt(2)-1)/(2*sqrt(2)),0)--cycle,grey);
+
fill(arcrot--(0,0)--cycle,grey);
 
draw(arc(origin,sqrt(2)/2+1/8,50+90*i,90*(i+1)-10),EndArrow);
 
draw(arc(origin,sqrt(2)/2+1/8,50+90*i,90*(i+1)-10),EndArrow);
 
}
 
}
 
draw(square^^square2);</asy>
 
draw(square^^square2);</asy>
  
−
For this square with side length 1, the distance from center to vertex is <math>r = \frac{1}{\sqrt{2}}</math>, hence the area is composed of a semicircle of radius <math>r</math>, plus <math>4</math> times a parallelogram with height <math>\frac{1}{2}</math> and base <math>\frac{\sqrt{2}}{2(1+\sqrt{2})}</math>. That is to say, the total area is <math>\frac{1}{2} \pi (1/\sqrt{2})^2 + 4 \frac{\sqrt{2}}{4(1+\sqrt{2})} = \boxed{\textbf{(C) } \frac{\pi}{4} + 2 - \sqrt{2}}</math>.
+
For this square with side length 1, the distance from center to vertex is <math>r = \frac{\sqrt{2}}{2}</math>, hence the area is composed of a semicircle of radius <math>r</math>, plus <math>4</math> times a parallelogram (or a kite with diagonals of <math>(\sqrt{2}-1)</math> and <math>r \text{ or} \frac{\sqrt{2}}{2}</math>) with height <math>\frac{1}{2}</math> and base <math>\frac{\sqrt{2}}{2(1+\sqrt{2})}</math>. That is to say, the total area is <math>\frac{1}{2} \pi \left(\frac{\sqrt{2}}{2}\right)^2 + 4 \frac{\sqrt{2}}{4(1+\sqrt{2})} = \boxed{\textbf{(C) } 2 - \sqrt{2} + \frac{\pi}{4}}</math>.
  
−
[[Image:AMC 10A 2013 -20.png|thumb|left|100px|]]
+
<asy>
 +
size(150);defaultpen(linewidth(0.8));
 +
path square=shift((-.5,-.5))*unitsquare,square2=rotate(45)*square;//fill(square^^square2,grey);
 +
for(int i=0;i<=3;i=i+1){path arcrot=arc(origin,sqrt(2)/2,45+90*i,90*(i+1));draw(arcrot);
 +
fill(arcrot--(0,0)--cycle,grey);}
 +
//draw(arc(origin,sqrt(2)/2+1/8,50+90*i,90*(i+1)-10),EndArrow);}
 +
draw(square^^square2);
 +
//draw((-.5,.5)--(.5,-.5)^^(0,sqrt(.5))--(0,-sqrt(.5)),dotted);draw((.5,.5)--(-.5,-.5),dotted);
 +
</asy>
 +
(To turn each dart-shaped piece into a parallelogram, cut along the dashed line and flip over one half.)
 +
<asy>
 +
size(150,Aspect);real r=sqrt(2);real b=2-2/r;
 +
draw((0,0)--(-1,1)--(b-1,1)--(0,r)--cycle);draw((0,1)--(b-1,1)--(b/2-1,1-b/2));draw((0,0)--(b-1,1),dashed);
 +
fill((2,0)--(b+1,1)--(b+2,0)--cycle,lightgray);draw((.5,.5)--(1,.5),EndArrow);
 +
draw((2,0)--(1,1)--(b+1,1)--(b+2,0)--(2,0)^^(b+1,1)--(b/2+1,1-b/2)^^(2,0)--(2+b/2,b/2));
 +
draw((2,0)--(b+1,1),dashed);
 +
</asy>
 +
Alternatively, you can move the dart-shaped piece to the other side and make a kite.
 +
<asy>
 +
size(75,Aspect);real r=sqrt(2);real b=2-2/r;
 +
draw((r-1,1)--(b-1,1));
 +
draw((0,0)--(b-1,1)--(0,r)--(r-1,1)--cycle);
 +
draw((0,r)--(0,0),dashed);
 +
</asy>
 +
 
 +
==Solution 2==
 +
<asy>
 +
size(200);
 +
defaultpen(linewidth(0.8));
 +
path square=shift((-.5,-.5))*unitsquare,square2=rotate(45)*square;
 +
for(int i=0;i<=6;i=i+1)
 +
{
 +
path arcrot=arc(origin,sqrt(2)/2,45+270*i,270*(i+1));
 +
draw(arcrot);
 +
}
 +
draw(square^^square2);</asy>
 +
<center><math>\textbf{(high res image; no labels)}</math></center>
 +
[[Image:AMC 10A 2013 20.jpg]]
 +
 
 +
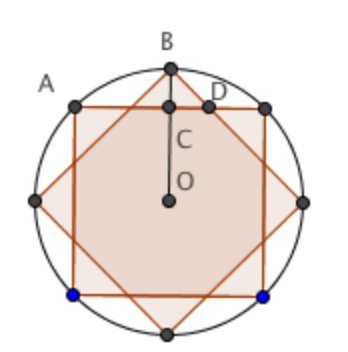
Let <math>O</math> be the center of the square and <math>C</math> be the intersection of <math>OB</math> and <math>AD</math>. The desired area consists of the unit square, plus <math>4</math> regions congruent to the region bounded by arc <math>AB</math>, <math>\overline{AC}</math>, and <math>\overline{BC}</math>, plus <math>4</math> triangular regions congruent to right triangle <math>BCD</math>. The area of the region bounded by arc <math>AB</math>, <math>\overline{AC}</math>, and <math>\overline{BC}</math> is <math>\frac{\text{Area of Circle}-\text{Area of Square}}{8}</math>. Since the circle has radius <math>\dfrac{1}{\sqrt {2}}</math>, the area of the region is <math>\dfrac{\dfrac{\pi}{2}-1}{8}</math>, so 4 times the area of that region is <math>\dfrac{\pi}{4}-\dfrac{1}{2}</math>. Now we find the area of <math>\triangle BCD</math>. <math>BC=BO-OC=\dfrac{\sqrt {2}}{2}-\dfrac{1}{2}</math>. Since <math>\triangle BCD</math> is a <math>45-45-90</math> right triangle, the area of <math>\triangle BCD</math> is <math>\dfrac{BC^2}{2}=\dfrac {\left (\dfrac {\sqrt {2}}{2}-\dfrac{1}{2} \right)^2}{2}</math>, so <math>4</math> times the area of <math>\triangle BCD</math> is <math>\dfrac{3}{2}-\sqrt {2}</math>. Finally, the area of the whole region is <math>1+ \left(\dfrac {3}{2}-\sqrt {2} \right) + \left(\dfrac{\pi}{4}-\dfrac{1}{2} \right)=\dfrac{\pi}{4}+2-\sqrt {2}</math>, which we can rewrite as <math>\boxed{\textbf{(C) }    2 - \sqrt{2} + \frac{\pi}{4}}</math>.
  
 
==See Also==
 
==See Also==

Latest revision as of 16:55, 23 July 2021

Problem

A unit square is rotated $45^\circ$ about its center. What is the area of the region swept out by the interior of the square?


$\textbf{(A)}\ 1 - \frac{\sqrt2}{2} + \frac{\pi}{4}\qquad\textbf{(B)}\ \frac{1}{2} + \frac{\pi}{4} \qquad\textbf{(C)}\ 2 - \sqrt2 + \frac{\pi}{4}\qquad\textbf{(D)}\ \frac{\sqrt2}{2} + \frac{\pi}{4} \qquad\textbf{(E)}\ 1 + \frac{\sqrt2}{4} + \frac{\pi}{8}$

Solution 1

First, we need to see what this looks like. Below is a diagram.

[asy] size(200); defaultpen(linewidth(0.8)); path square=shift((-.5,-.5))*unitsquare,square2=rotate(45)*square; fill(square^^square2,grey); for(int i=0;i<=3;i=i+1) { path arcrot=arc(origin,sqrt(2)/2,45+90*i,90*(i+1)); draw(arcrot); fill(arcrot--(0,0)--cycle,grey); draw(arc(origin,sqrt(2)/2+1/8,50+90*i,90*(i+1)-10),EndArrow); } draw(square^^square2);[/asy]

For this square with side length 1, the distance from center to vertex is $r = \frac{\sqrt{2}}{2}$, hence the area is composed of a semicircle of radius $r$, plus $4$ times a parallelogram (or a kite with diagonals of $(\sqrt{2}-1)$ and $r \text{ or} \frac{\sqrt{2}}{2}$) with height $\frac{1}{2}$ and base $\frac{\sqrt{2}}{2(1+\sqrt{2})}$. That is to say, the total area is $\frac{1}{2} \pi \left(\frac{\sqrt{2}}{2}\right)^2 + 4 \frac{\sqrt{2}}{4(1+\sqrt{2})} = \boxed{\textbf{(C) } 2 - \sqrt{2} + \frac{\pi}{4}}$.

[asy] size(150);defaultpen(linewidth(0.8)); path square=shift((-.5,-.5))*unitsquare,square2=rotate(45)*square;//fill(square^^square2,grey); for(int i=0;i<=3;i=i+1){path arcrot=arc(origin,sqrt(2)/2,45+90*i,90*(i+1));draw(arcrot); fill(arcrot--(0,0)--cycle,grey);} //draw(arc(origin,sqrt(2)/2+1/8,50+90*i,90*(i+1)-10),EndArrow);} draw(square^^square2); //draw((-.5,.5)--(.5,-.5)^^(0,sqrt(.5))--(0,-sqrt(.5)),dotted);draw((.5,.5)--(-.5,-.5),dotted); [/asy] (To turn each dart-shaped piece into a parallelogram, cut along the dashed line and flip over one half.) [asy] size(150,Aspect);real r=sqrt(2);real b=2-2/r; draw((0,0)--(-1,1)--(b-1,1)--(0,r)--cycle);draw((0,1)--(b-1,1)--(b/2-1,1-b/2));draw((0,0)--(b-1,1),dashed); fill((2,0)--(b+1,1)--(b+2,0)--cycle,lightgray);draw((.5,.5)--(1,.5),EndArrow); draw((2,0)--(1,1)--(b+1,1)--(b+2,0)--(2,0)^^(b+1,1)--(b/2+1,1-b/2)^^(2,0)--(2+b/2,b/2)); draw((2,0)--(b+1,1),dashed); [/asy] Alternatively, you can move the dart-shaped piece to the other side and make a kite. [asy] size(75,Aspect);real r=sqrt(2);real b=2-2/r; draw((r-1,1)--(b-1,1)); draw((0,0)--(b-1,1)--(0,r)--(r-1,1)--cycle); draw((0,r)--(0,0),dashed); [/asy]

Solution 2

[asy] size(200); defaultpen(linewidth(0.8)); path square=shift((-.5,-.5))*unitsquare,square2=rotate(45)*square; for(int i=0;i<=6;i=i+1) { path arcrot=arc(origin,sqrt(2)/2,45+270*i,270*(i+1)); draw(arcrot); } draw(square^^square2);[/asy]

$\textbf{(high res image; no labels)}$

AMC 10A 2013 20.jpg

Let $O$ be the center of the square and $C$ be the intersection of $OB$ and $AD$. The desired area consists of the unit square, plus $4$ regions congruent to the region bounded by arc $AB$, $\overline{AC}$, and $\overline{BC}$, plus $4$ triangular regions congruent to right triangle $BCD$. The area of the region bounded by arc $AB$, $\overline{AC}$, and $\overline{BC}$ is $\frac{\text{Area of Circle}-\text{Area of Square}}{8}$. Since the circle has radius $\dfrac{1}{\sqrt {2}}$, the area of the region is $\dfrac{\dfrac{\pi}{2}-1}{8}$, so 4 times the area of that region is $\dfrac{\pi}{4}-\dfrac{1}{2}$. Now we find the area of $\triangle BCD$. $BC=BO-OC=\dfrac{\sqrt {2}}{2}-\dfrac{1}{2}$. Since $\triangle BCD$ is a $45-45-90$ right triangle, the area of $\triangle BCD$ is $\dfrac{BC^2}{2}=\dfrac {\left (\dfrac {\sqrt {2}}{2}-\dfrac{1}{2} \right)^2}{2}$, so $4$ times the area of $\triangle BCD$ is $\dfrac{3}{2}-\sqrt {2}$. Finally, the area of the whole region is $1+ \left(\dfrac {3}{2}-\sqrt {2} \right) + \left(\dfrac{\pi}{4}-\dfrac{1}{2} \right)=\dfrac{\pi}{4}+2-\sqrt {2}$, which we can rewrite as $\boxed{\textbf{(C) } 2 - \sqrt{2} + \frac{\pi}{4}}$.

See Also

2013 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 19 		Followed by
Problem 21
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2013_AMC_10A_Problems/Problem_20&oldid=159012"