Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 JMPSC Sprint Problems/Problem 16"

(→‎Problem)
 
(3 intermediate revisions by 2 users not shown)
Line 6: Line 6:
  
 
==Solution==
 
==Solution==
 +
 +
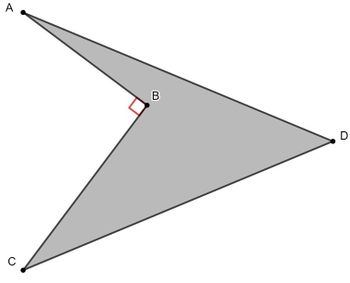
Notice that <math>[ABCD] = [ADC] - [ABC]</math> and <math>AC = \sqrt{12^2 + 16^2} = 20</math> by the Pythagorean Thereom. We then have that the area of triangle of <math>ADC</math> is <math>\frac{20 \cdot \sqrt{26^2 - 10^2}}{2} = 240</math>, and the area of triangle <math>ABC</math> is <math>\frac{12 \cdot 16}{2} = 96</math>, so the area of quadrilateral <math>ABCD</math> is <math>240 - 96 = 144</math>.
 +
 +
~Mathdreams
 +
 +
== Solution 2 ==
 +
<cmath>[ACD] = \frac{24 \cdot 20}{2}=240</cmath>
 +
<cmath>[ABC] = \frac{12 \cdot 16}{2}=96</cmath>
 +
Therefore, <math>[ABCD] = 240-96=144</math>
 +
 +
- kante314 -
 +
 +
==See also==
 +
#[[2021 JMPSC Sprint Problems|Other 2021 JMPSC Sprint Problems]]
 +
#[[2021 JMPSC Sprint Answer Key|2021 JMPSC Sprint Answer Key]]
 +
#[[JMPSC Problems and Solutions|All JMPSC Problems and Solutions]]
 +
{{JMPSC Notice}}

Latest revision as of 09:39, 12 July 2021

Problem

$ABCD$ is a concave quadrilateral with $AB = 12$, $BC = 16$, $AD = CD = 26$, and $\angle ABC=90^\circ$. Find the area of $ABCD$.

Sprint16.jpg

Solution

Notice that $[ABCD] = [ADC] - [ABC]$ and $AC = \sqrt{12^2 + 16^2} = 20$ by the Pythagorean Thereom. We then have that the area of triangle of $ADC$ is $\frac{20 \cdot \sqrt{26^2 - 10^2}}{2} = 240$, and the area of triangle $ABC$ is $\frac{12 \cdot 16}{2} = 96$, so the area of quadrilateral $ABCD$ is $240 - 96 = 144$.

~Mathdreams

Solution 2

\[[ACD] = \frac{24 \cdot 20}{2}=240\] \[[ABC] = \frac{12 \cdot 16}{2}=96\] Therefore, $[ABCD] = 240-96=144$

- kante314 -

See also

  1. Other 2021 JMPSC Sprint Problems
  2. 2021 JMPSC Sprint Answer Key
  3. All JMPSC Problems and Solutions

The problems on this page are copyrighted by the Junior Mathematicians' Problem Solving Competition. JMPSC.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_JMPSC_Sprint_Problems/Problem_16&oldid=158214"