Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 JMPSC Accuracy Problems/Problem 3"

(→‎Problem)
 
(6 intermediate revisions by 3 users not shown)
Line 2: Line 2:
  
 
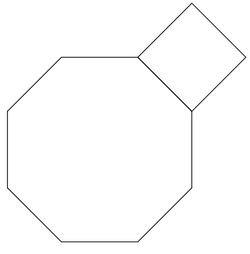
In a regular octagon, the sum of any three consecutive sides is <math>90.</math> A square is constructed using one of the sides of this octagon. What is the area of the square?
 
In a regular octagon, the sum of any three consecutive sides is <math>90.</math> A square is constructed using one of the sides of this octagon. What is the area of the square?
 +
<center>
 +
[[File:Octagonsquare.jpg|250px]]
 +
</center>
 +
 +
==Solution==
 +
 +
We are given that the sum of any three sides of the octagon is 90, and since the octagon is regular, we know that all sides are equal. Thus, each side of the octagon must equal to <math>\frac{90}{3} = 30</math>. Since one side of the square shares a side with the octagon, we know the side lengths of the square are also 30. Thus, our answer is <math>30^2 = \boxed{900}</math>
 +
 +
~Bradygho
 +
 +
==Solution 2==
 +
We have each side of the octagon is <math>s</math>, so <math>3s=90</math>, or <math>s=30</math>. This means the area of the square is <math>30^2=\boxed{900}</math>
 +
 +
~Geometry285
 +
  
−
[[File:Octagonsquare.jpg|200px]]
 
  
−
==Solution==
+
==See also==
 +
#[[2021 JMPSC Accuracy Problems|Other 2021 JMPSC Accuracy Problems]]
 +
#[[2021 JMPSC Accuracy Answer Key|2021 JMPSC Accuracy Answer Key]]
 +
#[[JMPSC Problems and Solutions|All JMPSC Problems and Solutions]]
 +
{{JMPSC Notice}}

Latest revision as of 16:23, 11 July 2021

Problem

In a regular octagon, the sum of any three consecutive sides is $90.$ A square is constructed using one of the sides of this octagon. What is the area of the square?

Octagonsquare.jpg

Solution

We are given that the sum of any three sides of the octagon is 90, and since the octagon is regular, we know that all sides are equal. Thus, each side of the octagon must equal to $\frac{90}{3} = 30$. Since one side of the square shares a side with the octagon, we know the side lengths of the square are also 30. Thus, our answer is $30^2 = \boxed{900}$

~Bradygho

Solution 2

We have each side of the octagon is $s$, so $3s=90$, or $s=30$. This means the area of the square is $30^2=\boxed{900}$

~Geometry285


See also

  1. Other 2021 JMPSC Accuracy Problems
  2. 2021 JMPSC Accuracy Answer Key
  3. All JMPSC Problems and Solutions

The problems on this page are copyrighted by the Junior Mathematicians' Problem Solving Competition. JMPSC.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_JMPSC_Accuracy_Problems/Problem_3&oldid=158064"